Gray-Scott Reaction-Diffusion Engine

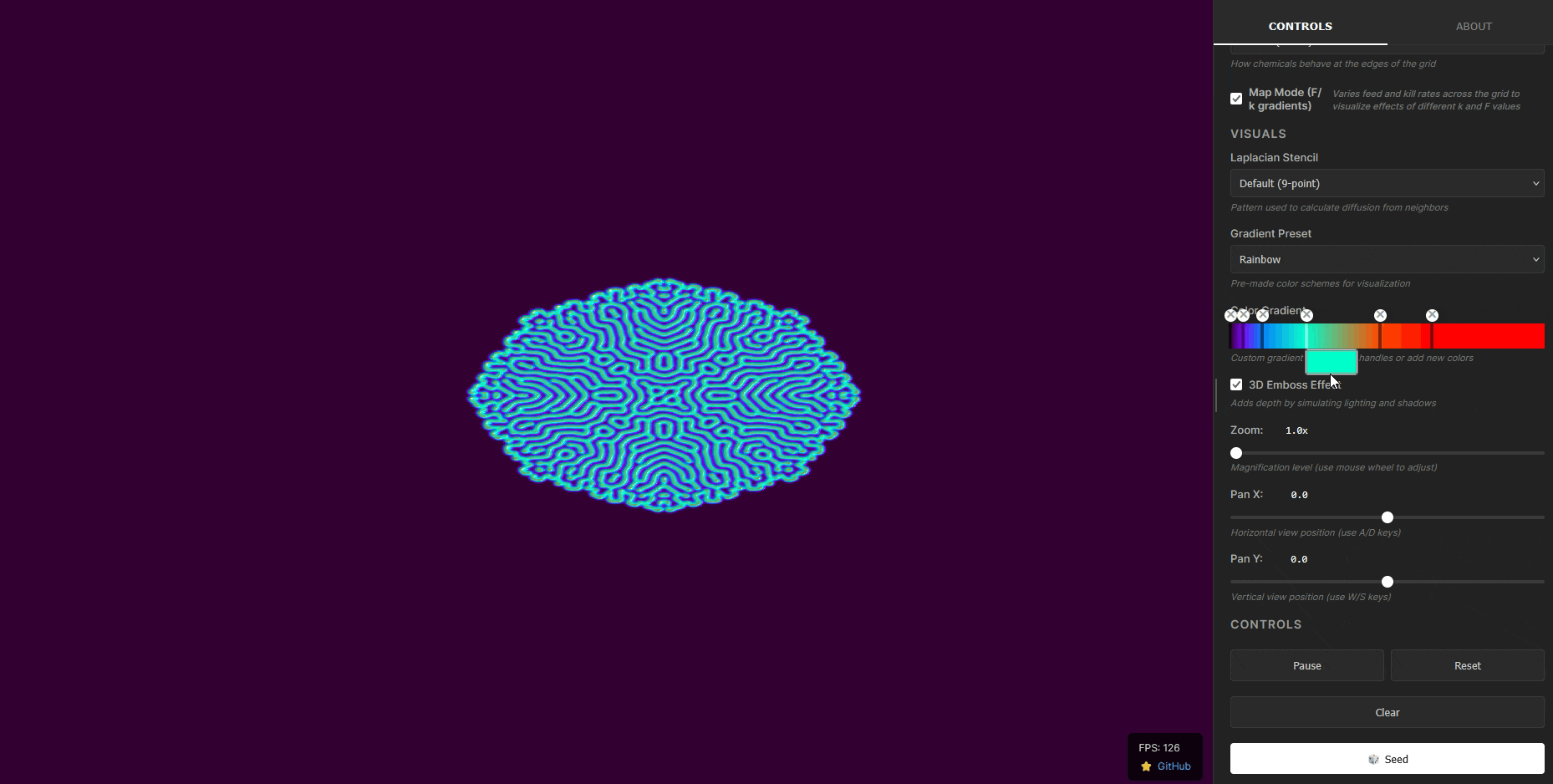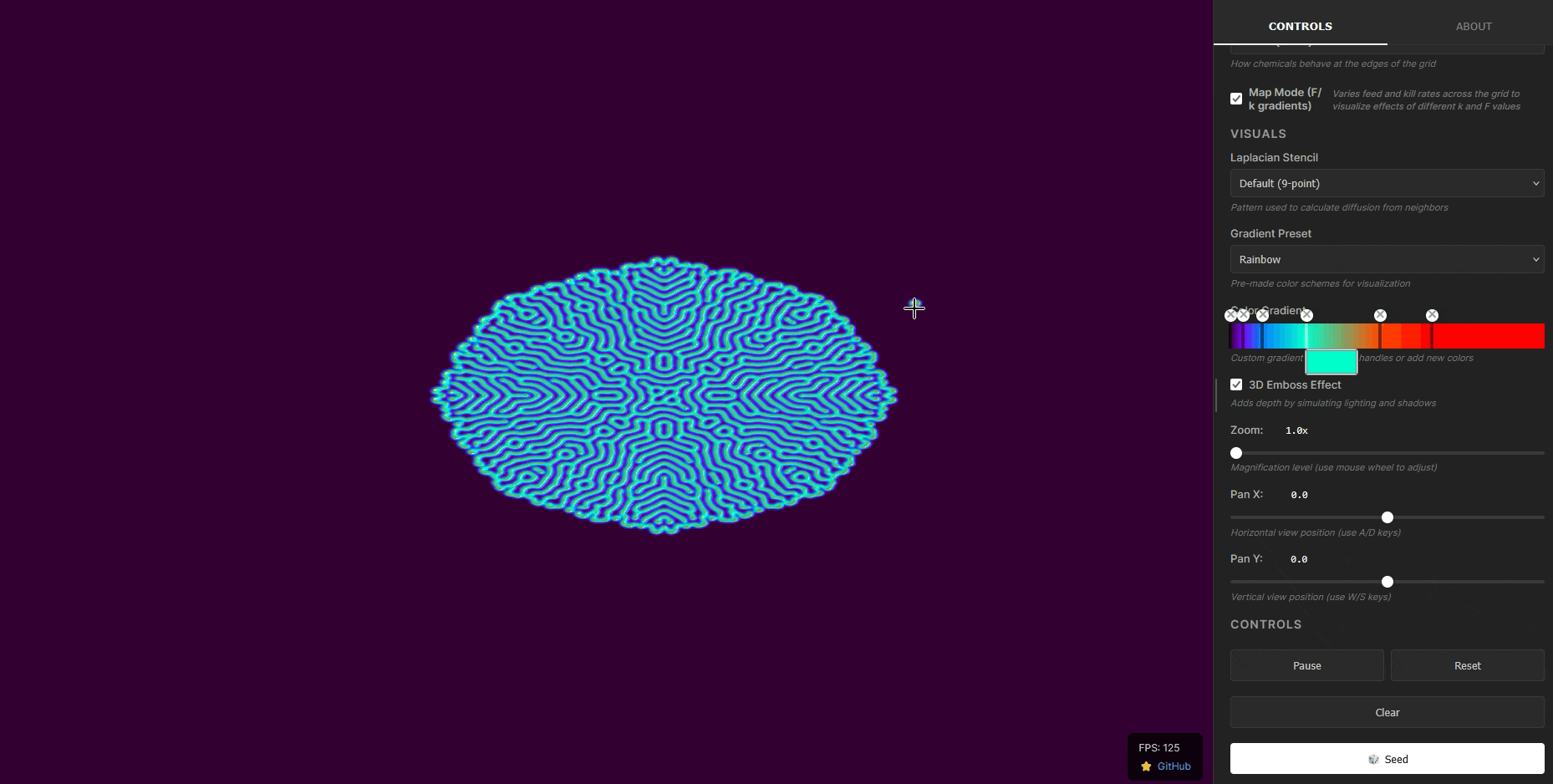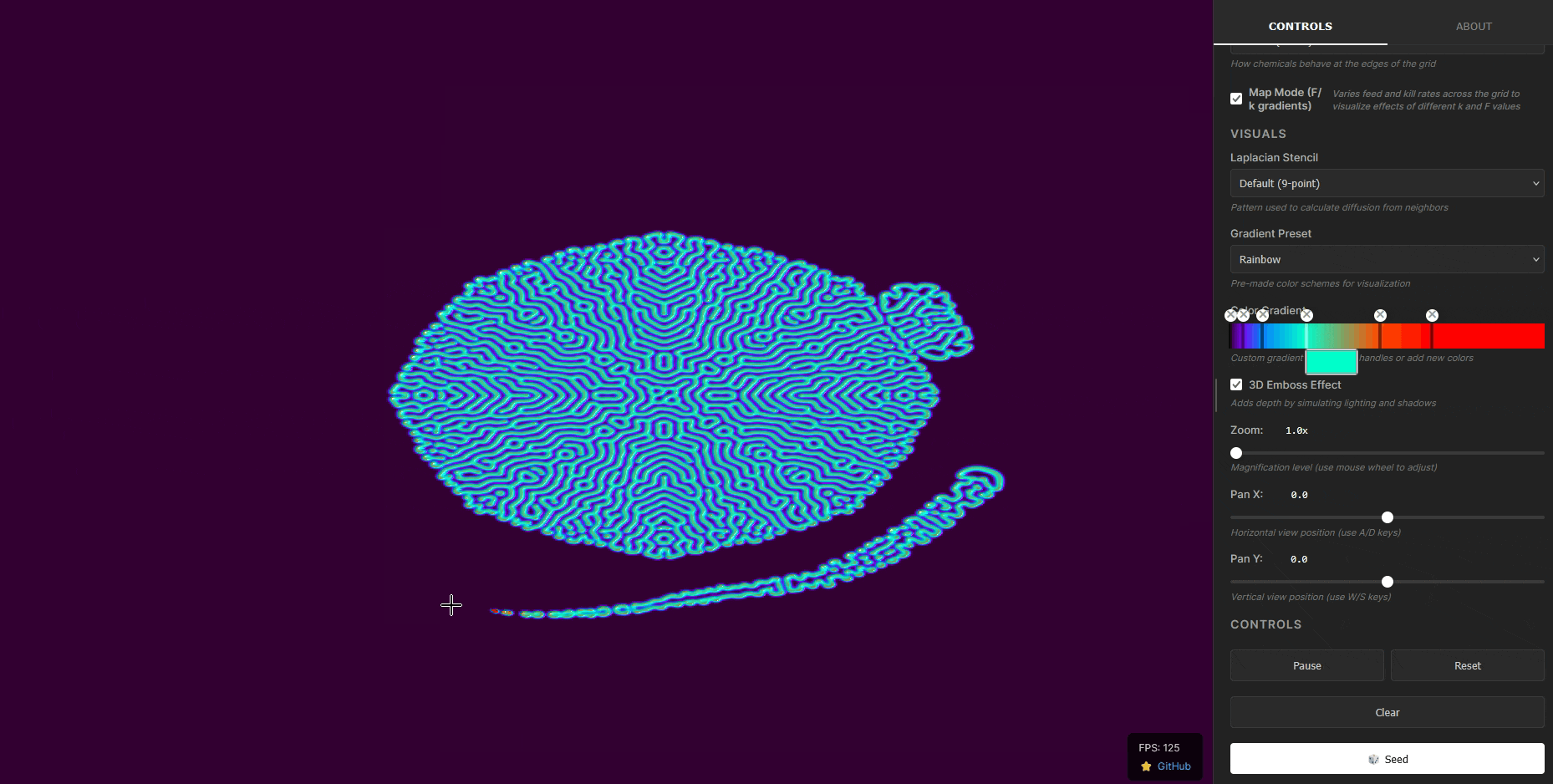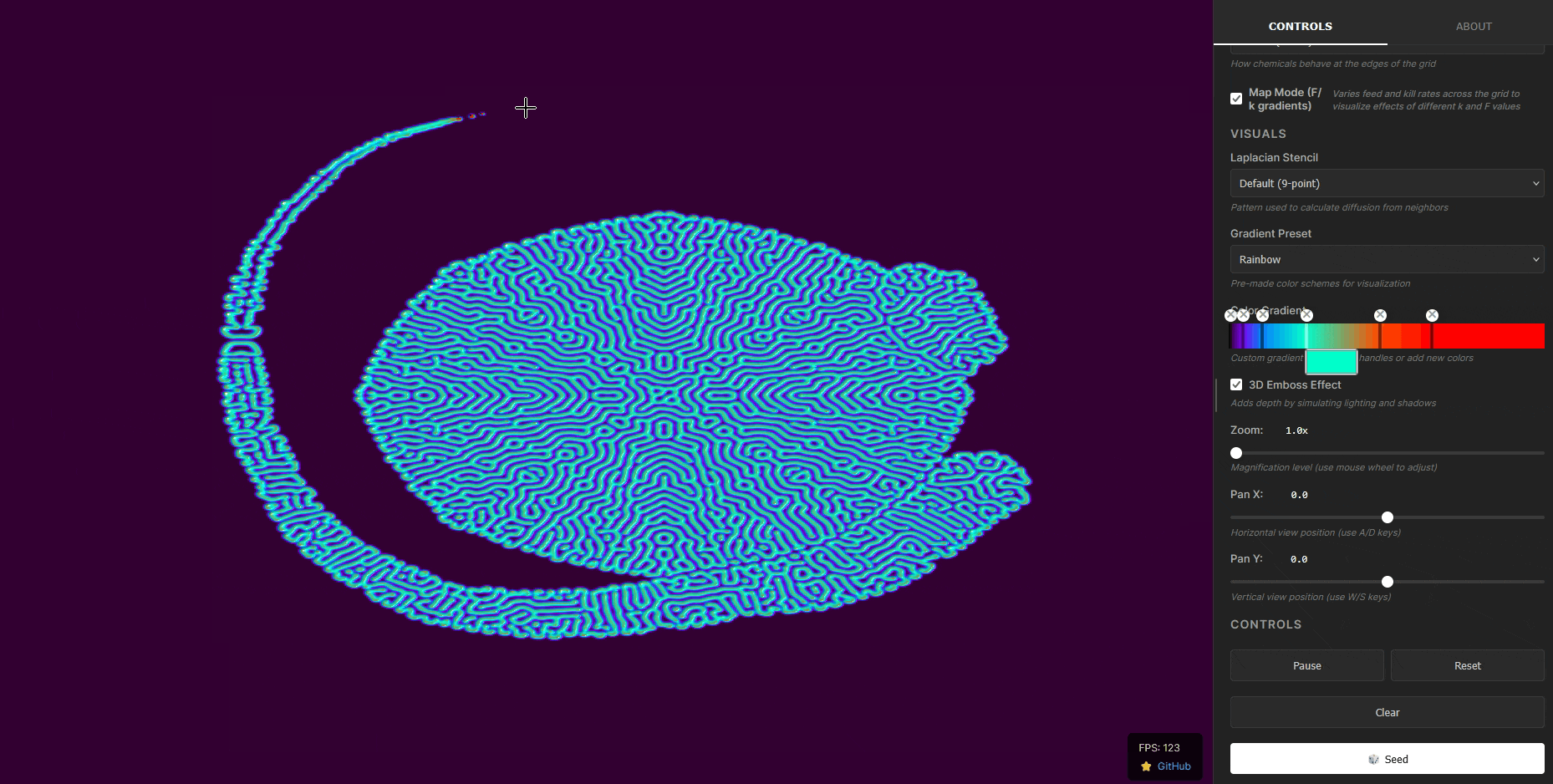
A GPU-accelerated WebGPU implementation of the Gray-Scott reaction-diffusion system, capable of generating complex spatial patterns from simple chemical interactions. Compiles to WebAssembly for near-native browser performance.

Introduction

The Gray–Scott model is a reaction–diffusion system used to look at how simple chemical interactions can generate complex patterns. It describes the evolution of two chemical species, U and V, diffusing across a surface while undergoing an autocatalytic reaction. Unlike linear diffusion equations, which smooth out disturbances, the Gray–Scott system is highly nonlinear and can produce stable spots, stripes, waves, and other very interesting Turing patterns.

Because of its non-linear nature, we must simulate the system numerically. Here, we simulate it on a 2D grid using finite difference approximations for the diffusion terms and explicit time-stepping for the reactions. Almost like a cellular automaton, but instead of having discrete states, each cell holds continuous concentration values for chemicals U and V.

Reaction–Diffusion Model

The Gray–Scott system models a simplified autocatalytic reaction:

• U + 2V → 3V (autocatalysis)
• V → P (decay)

Here, U is fed into the system at a constant rate, while V is the reactant that autocatalytically converts U into more of itself. Because of these interactions and imbalances, small changes in the concentrations of U and V can grow and lead to complex patterns.

When diffusion is included and the system is treated as a continuous 2D medium, the concentrations U(x,y,t) and V(x,y,t)—meaning 'the concentration of U or V at position (x,y) and time t'—evolve according to the following pair of partial differential equations:

$$ \frac{\partial U}{\partial t} = D_U \nabla^2 U - UV^2 + F(1 - U) $$ $$ \frac{\partial V}{\partial t} = D_V \nabla^2 V + UV^2 - (F + k)V $$

Where:

• D_U and D_V are the diffusion rates of species U and V
• F is the feed rate of U
• k is the kill rate of V
• $\nabla^2$ is the Laplacian operator, which captures how the concentration at a point differs from its neighbors

Understanding the Terms

1. Diffusion term ($D_u \nabla^2 U$): Represents how chemicals spread out over time, smoothing concentration differences.
2. Reaction term $(\pm UV^2)$: Represents the autocatalytic reaction where species U is consumed to produce more of species V.
3. Feed/Kill terms: Represents the feed and removal rate of chemicals from the system. This maintains a non-equilibrium state, which is necessary for forming those interesting patterns.

Technical Details

This project has been an amazing opportunity to learn all about GPU programming, shaders, webassembly, and numerical simulation. In the end, I was able to create a real-time interactive simulation that runs entirely in the browser. It's been a lot of fun to play with, and I've spent hours just messing around with the parameters to see the different patterns that emerge.

• Built with Rust and WebGPU via wgpu
• Compiled to WebAssembly for browser execution
• Uses compute shaders for parallel simulation
• Real-time gradient updates and visual effects

Building from Source

Prerequisites

• Rust
• wasm-pack
• A modern web browser

Build Steps

# Install wasm-pack if needed
cargo install wasm-pack

# Build the WebAssembly module
wasm-pack build --target web

# Serve locally (use any static file server---whatever)
python -m http.server 8000

Then open http://localhost:8000 in browser that supports WebGPU.

References

• Reaction-Diffusion by the Gray-Scott Model: Pearson's Parametrization
• Karl Sims' Reaction-Diffusion Tutorial
• Learn Wgpu

License

This project is open source and available under the MIT License.