-
Notifications
You must be signed in to change notification settings - Fork 18
Home
This project provides Java implementations of more than 35 algorithms for generating so called "perfect mazes" (which are just spanning trees of undirected graphs).
On the web, many maze generation implementations in all possible programming languages can be found. The popularity of these algorithms probably comes from the fact that mazes and their creation processes are visually appealing and not really difficult to implement. The most popular algorithm seems to be "recursive backtracking" which is random depth-first traversal of a graph.
On the other hand, there are only a few websites where the whole spectrum of maze creation algorithms is investigated. One prominent example is this blog where Jamis Buck presents the most popular maze algorithms together with Ruby/Javascript implementations. Reading his blog led myself to investigate this topic too.
Initially, I just intended to implement some of these algorithms to learn about the (then) new Java features (streams, lambda expressions). I also wanted to implement the needed data structures (graph, grid graph, union-find, ...) not just in an "ad-hoc" fashion. The maze algorithm implementations should become pure graph algorithms without any UI or animation related parts. The underlying algorithm, for example a minimum-spanning tree algorithm, should remain recognizable in the maze generator code. Avoiding dependencies to UI frameworks should help in making the code more reusable. For example, the animated GIF images below have been created using a grid graph observer which takes snapshots of the maze while being created.
In the end, all the algorithms presented in Jamis Buck's blog and even some new algorithms got implemented.
One new algorithm is a modification of Eller's algorithm that in contrast to the original doesn't generate the maze row-wise but from the center of the grid towards the outer borders. The resulting maze however is heavily biased.
Other new algorithms are variations of David B. Wilson's uniform spanning tree algorithm. They result from the different possibilities for selecting the random walk start cells. Because the order in which the random walk start cells are selected is arbitrary, there are lots of interesting choices: For example, one can start the random walks in the order defined by a space-filling curve like Hilbert, Peano or Moore curves.
You can also use any other interesting pattern for filling a grid. In any case you'll get a visually appealing maze creation process.
The companion repository graph-search contains a number of path finding algorithms for "solving" the generated mazes:
- Breadth-First Search
- Depth-First Search
- Greedy Best-First Search
- Hill Climbing DFS
- A*
- Uniform-Cost Search (Dijkstra).
- Bidirectional BFS, Dijkstra, A*
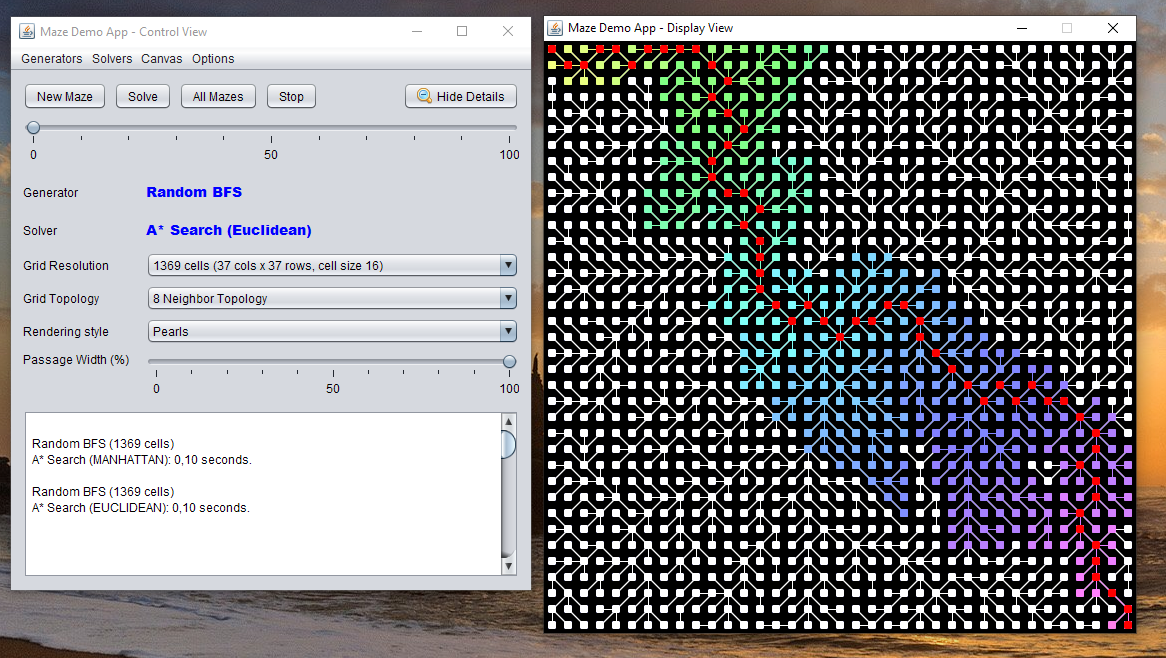
The included demo application demonstrates all implemented maze generators and path finders. Using a control panel you can interactively select the generation algorithm, path finder, grid resolution and rendering style ("walls", "passages").
Maze generators are sometimes separated into "wall builders" and "passage carvers". I prefer the graph theoretic view of removing ("building walls") and adding edges ("carving a passage"). Interpreting a vertex as a "room" and a missing edge as a "wall" is just a matter of drawing the graph:
Click to show picture

To achieve the mentioned goals, I implemented
- an API for graph and 2D-grid data structures
- a space-efficient implementation of a 2D-grid with ability to store cell and edge content
- a publish-subscribe mechanism for observing graph/grid operations and different path finding algorithms.
This is the maze generator derived from Kruskal's minimum spanning tree algorithm:
public void createMaze(int x, int y) {
var forest = new Partition<>();
var fullGrid = fullGrid(grid.numCols(), grid.numRows(), grid.getTopology(), UNVISITED, 0);
permute(fullGrid.edges()).forEach(edge -> {
int u = edge.either(), v = edge.other();
if (forest.union(u, v)) {
grid.addEdge(u, v);
grid.set(u, COMPLETED); // only for visualization
grid.set(v, COMPLETED); // only for visualization
}
});
}Anybody familiar with the Kruskal algorithm will immediately recognize it in this code. The difference is that in the maze generator the edges of a (full) grid are selected in random order where the original MST algorithm greedily selects the minimum cost edge in each step.
Implemented maze generation algorithms:
Click to show picture

Click to show picture

Click to show picture

Growing tree (always first vertex selected)
Click to show picture

Growing tree (always last vertex selected)
Click to show picture

Growing tree (always random vertex selected)
Click to show picture

Growing tree (last or random vertex selected)
Click to show picture

Click to show picture

Click to show picture

Click to show picture

Different variants are implemented using different path finder implementations for checking if two vertices are connected.
Click to show picture

Click to show picture

Houston (A hybrid of Aldous-Broder and Wilson's)
Wilson's algorithm (16 different variants)
Click to show picture

Click to show picture

Click to show picture

Click to show picture

Click to show picture

Click to show picture

Armin's algorithm (like Eller's but growing the maze inside-out)
Click to show picture

Click to show picture

Click to show picture

Click to show picture

Click to show picture

The graph library contains (among others) the following path finder implementations:
- Breadth-First-Search
- Depth-First-Search
- (Greedy) Best-First-Search
- Hill Climbing
- A* Search
- Uniform-Cost Search (Dijkstra).
The "informed" path finders can be used with arbitrary heuristics, for example Euclidean, Manhattan and Chebyshev distance to target.