A PyTorch module for vectorized and differentiable parametric curves with learnable coefficients, such as a B-Spline curve with learnable control points.

Use cases

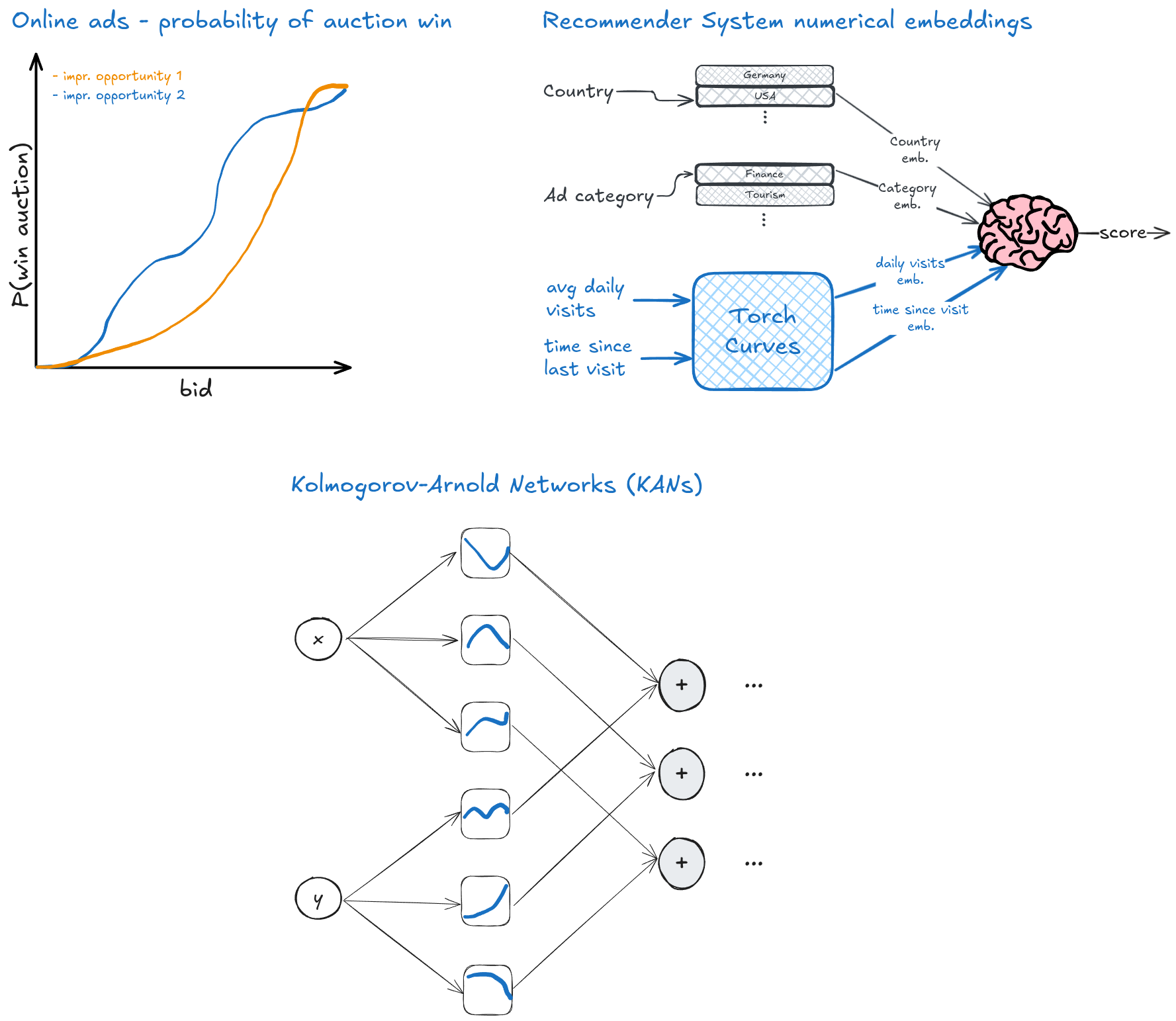
Turns out all the above use cases have one thing in common - they can all be expressed using learnable parametric curves, and this the tool this library provides.

Docs

• Documentation site.
• Example notebooks for you to try our

Features

• Differentiable: Custom autograd function ensures gradients flow properly through the curve evaluation.
• Vectorized: Vectorized operations for efficient batch and multi-curve evaluation.
• Efficient numerics: Clenshaw recursion for polynomials, Cox-DeBoor for splines.

Installation

With pip:

pip install torchcurves

With uv:

uv add torchcurves

Use cases

There are examples in the docs/examples directory showing how to build models using this library. Here we show some simple code snippets to appreciate the library.

Use case 1 - continuous embeddings

import torchcurves as tc
from torch import nn
import torch


def Net(nn.Module):
    def __init__(self, num_categorical, num_numerical, dim, num_knots=10):
        super().__init__()
        self.cat_emb = nn.Embedding(num_categorical, dim)
        self.num_emb = tc.BSplineCurve(num_numerical, dim, knots_config=num_knots)
        self.embedding_based_model = MySuperDuperModel()

    def forward(self, x_categorical, x_numerical):
        embeddings = torch.cat([
            self.cat_emb(x_categorical),
            self.num_emb(x_numerical)
        ], axis=-2)
        return self.embedding_based_model(embeddings)

Use case 2 - monotone functions

Working on online advertising, and want to model the probability of winning an ad auction given the bid? We know higher bids must result in a higher win probability - we need a monotone function. Turns out B-Splines are monotone if their coefficient vectors are monotone. Want an increasing function? Just make sure the increasing - so let's use it.

Below is an example with an auction encoder that encodes the auction into a vector, we then transform it to an increasing vector, and use it as the coefficient vector for a B-Spline curve.

import torch
from torch import nn
import torchcurves.functional as tcf


class AuctionWinModel(nn.Module):
    def __init__(self, num_auction_features, num_bid_coefficients):
        self.auction_encoder = make_auction_encoder(  # example - an MLP, a transformer, etc.
            input_features=num_auction_features,
            output_features=num_bid_coefficients,
        )
        self.spline_knots = nn.Buffer(tcf.uniform_augmented_knots(
            n_control_points=num_bid_coefficients,
            degree=3,
            k_min=0,
            k_max=1
        ))

    def forward(self, auction_features, bids):
        # map auction features to increasing spline coefficients
        spline_coeffs = self._make_increasing(self.auction_encoder(auction_features))

        # map bids to [0, 1] using the arctan (or any other) normalization
        mapped_bid = tcf.arctan(bids)

        # evaluate the spline at the mapped bids, treating each
        # mini-batch sample as a separate curve
        return tcf.bspline_curves(
            mapped_bid.unsqueeze(0),     # 1 x B (B curves in 1 dimension)
            spline_coeffs.unsqueeze(-1), # B x C x 1 (B curves with C coefs in 1 dimension)
            self.knots,
            degree=3
        )

    def _make_increasing(self, x):
        # transform a mini-batch of vectors to a mini-batch of increasing vectors
        initial = x[..., :1]
        increments = nn.functional.softplus(x[..., 1:])
        concatenated = torch.concat((initial, increments), dim=-1)
        return torch.cumsum(concatenated, dim=-1)

Now we can train the model to predict the probability of winning auctions given auction features and bid:

import torch.functional as F

for auction_features, bids, win_labels in train_loader:
    win_logits = model(auction_features, bids)
    loss = F.binary_cross_entropy_with_logits(  # or any loss we desire
        win_logits,
        win_labels
    )

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

Use case 3 - Kolmogorov-Arnold networks

A KAN [1] based on the B-Spline basis, along the lines of the original paper:

import torchcurves as tc
from torch import nn

input_dim = 2
intermediate_dim = 5
num_control_points = 10

kan = nn.Sequential(
    # layer 1
    tc.BSplineCurve(input_dim, intermediate_dim, knots_config=num_control_points),
    tc.Sum(dim=-2),
    # layer 2
    tc.BSplineCurve(intermediate_dim, intermediate_dim, knots_config=num_control_points),
    tc.Sum(dim=-2),
    # layer 3
    tc.BSplineCurve(intermediate_dim, 1, knots_config=num_control_points),
    tc.Sum(dim=-2),
)

Yes, we know the original KAN paper used a different curve parametrization, B-Spline + arcsinh, but the whole point of this repo is showing that KAN activations can be parametrized in arbitrary ways.

For example, here is a KAN based on Legendre polynomials of degree 5:

import torchcurves as tc
from torch import nn

input_dim = 2
intermediate_dim = 5
degree = 5

kan = nn.Sequential(
    # layer 1
    tc.LegendreCurve(input_dim, intermediate_dim, degree=degree),
    tc.Sum(dim=-2),
    # layer 2
    tc.LegendreCurve(intermediate_dim, intermediate_dim, degree=degree),
    tc.Sum(dim=-2),
    # layer 3
    tc.LegendreCurve(intermediate_dim, 1, degree=degree),
    tc.Sum(dim=-2),
)

Since KANs are the primary use case for the tc.Sum() layer, we can omit the dim=-2 argument, but it is provided here for clarity.

Advanced features

The curves we provide here typically rely on their inputs to lie in a compact interval, typically [-1, 1]. Arbitrary inputs need to be normalized to this interval. We provide two simple out-of-the-box normalization strategies described below.

Rational scaling

This is the default strategy — this strategy computes

$$x \to \frac{x}{\sqrt{s^2 + x^2}},$$

and is based on the paper

Wang, Z.Q. and Guo, B.Y., 2004. Modified Legendre rational spectral method for the whole line. Journal of Computational Mathematics, pp.457-474.

In Python it looks like this:

tc.BSplineCurve(curve_dim, normalization_fn='rational', normalization_scale=s)

Arctan scaling

This strategy computes

$$x \to \frac{2}{\pi} \arctan(x / s).$$

This kind of scaling function, up to constants, is the CDF of the Cauchy distribution. It is useful when our inputs are assumed to be heavy tailed.

In Python it looks like this:

tc.BSplineCurve(curve_dim, normalization_fn='arctan', normalization_scale=s)

Clamping

The inputs are simply clipped to [-1, 1] after scaling, i.e.

$$x \to \max(\min(1, x / s), -1)$$

In Python it looks like this:

tc.BSplineCurve(curve_dim, normalization_fn='clamp', normalization_scale=s)

Custom normalization

Provide a custom function that maps its input to the designated range after scaling. Example:

def erf_clamp(x: Tensor, scale: float = 1, out_min: float = -1, out_max: float = 1) -> Tensor:
    mapped = torch.special.erf(x / scale)
    return ((mapped + 1) * (out_max - out_min)) / 2 + out_min

tc.BSplineCurve(curve_dim, normalization_fn=erf_clamp, normalization_scale=s)

Example: B-Spline KAN with clamping

A KAN based on rationally scaled B-Spline basis with the default scale of $s=1$:

spline_kan = nn.Sequential(
    # layer 1
    tc.BSplineCurve(input_dim, intermediate_dim, knots_config=knots, normalization_fn='clamp'),
    tc.Sum(),
    # layer 2
    tc.BSplineCurve(intermediate_dim, intermediate_dim, knots_config=knots, normalization_fn='clamp'),
    tc.Sum(),
    # layer 3
    tc.BSplineCurve(intermediate_dim, 1, knots_config=knots, normalization_fn='clamp'),
    tc.Sum(),
)

Legendre KAN with rational clamping

import torchcurves as tc
from torch import nn

input_dim = 2
intermediate_dim = 5
degree = 5

config = dict(degree=degree, normalization_fn="clamp")
kan = nn.Sequential(
    # layer 1
    tc.LegendreCurve(input_dim, intermediate_dim, **config),
    tc.Sum(),
    # layer 2
    tc.LegendreCurve(intermediate_dim, intermediate_dim, **config),
    tc.Sum(),
    # layer 3
    tc.LegendreCurve(intermediate_dim, 1, **config),
    tc.Sum(),
)

Development

Development Installation

Using uv (recommended):

# Clone the repository
git clone https://github.com/alexshtf/torchcurves.git
cd torchcurves

# Create virtual environment and install
uv venv
uv sync --all-groups

Running Tests

# Run all tests
uv run pytest

# Run with coverage
uv run pytest --cov=torchcurves

# Run specific test file
uv run pytest tests/test_bspline.py -v

Performance Benchmarks

This project includes opt-in performance benchmarks (forward and backward passes) using pytest-benchmark.

Location: benchmarks/

Run benchmarks:

# Run all benchmarks
uv run pytest benchmarks -q

# Or select only perf-marked tests if you mix them into tests/
uv run pytest -m perf -q

CUDA timing notes: We synchronize before/after timed regions for accurate GPU timings.

Compare runs and fail CI on regressions:

# Save a baseline
uv run pytest benchmarks --benchmark-save=legendre_baseline

# Compare current run to baseline (fail if mean slower by 10% or more)
uv run pytest benchmarks --benchmark-compare --benchmark-compare-fail=mean:10%

Export results:

uv run pytest benchmarks --benchmark-json=bench.json

Building the docs

# Prepare API docs
cd docs
make html

Citation

If you use this package in your research, please cite:

@software{torchcurves,
  author = {Shtoff, Alex},
  title = {torchcurves: Differentiable Parametric Curves in PyTorch},
  year = {2025},
  publisher = {GitHub},
  url = {https://github.com/alexshtf/torchcurves}
}

References

[1]: Ziming Liu, Yixuan Wang, Sachin Vaidya, Fabian Ruehle, James Halverson, Marin Soljacic, Thomas Y. Hou, Max Tegmark. "KAN: Kolmogorov–Arnold Networks." ICLR (2025).
[2]: Juergen Schmidhuber. "Learning to control fast-weight memories: An alternative to dynamic recurrent networks." Neural Computation, 4(1), pp.131-139. (1992)
[3]: Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Łukasz Kaiser, and Illia Polosukhin. "Attention is all you need." Advances in neural information processing systems 30 (2017).
[4]: Alex Shtoff, Elie Abboud, Rotem Stram, and Oren Somekh. "Function Basis Encoding of Numerical Features in Factorization Machines." Transactions on Machine Learning Research.
[5]: Rügamer, David. "Scalable Higher-Order Tensor Product Spline Models." In International Conference on Artificial Intelligence and Statistics, pp. 1-9. PMLR, 2024.
[6]: Steffen Rendle. "Factorization machines." In 2010 IEEE International conference on data mining, pp. 995-1000. IEEE, 2010.