-
Notifications
You must be signed in to change notification settings - Fork 2
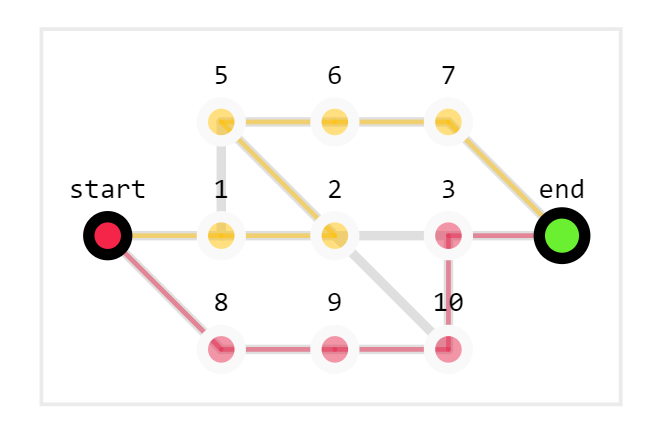
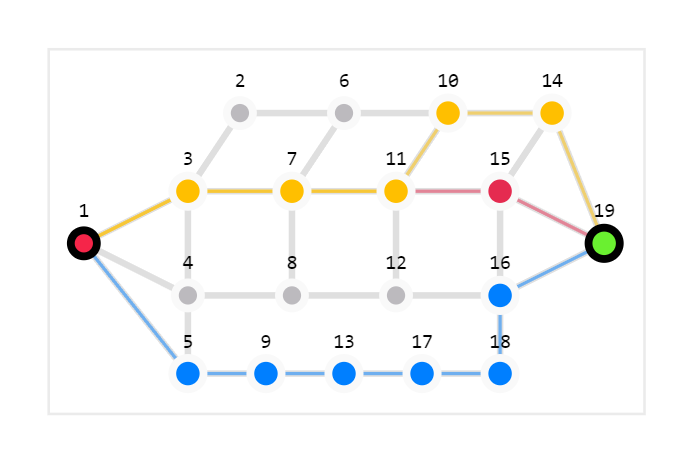
Failed try with "Suurballe BFS"
In the lem in we using Suurballe's algorithm
If you do not know about the Suurballe algorithm, there is no point in reading further. Read about this algorithm, links below. Suurballe's algorithm Links:
anthill - Stores information about the graph, the data being read, and the result.
// Graph
type anthill struct {
FieldInfo *fieldInfo
AntsCount int
Start, End string
Rooms map[string]*room
StepsCount int
Result *Result
}room - Stores information about room.
In the suurballe algorithm, the vertices used for the path are doubled. And so that we don't create more vertices after finding the path, we use markers that simulate 2 graphs. (Some kind of optimization).
By default, all relationships are written to PathOut
// Node
type room struct {
Name string // Name
X, Y int // Coordinates
PathsIn, PathsOut map[string]*room // Using For Surballe algo
MarkedIn, MarkedOut bool // For know using rooms
ParentIn, ParentOut *room // Using For Surballe algo
UsingOnPath bool // Means - Is Using On Finded Paths
}The Result records the results of the Paths found and the number of ants. These two parameters are needed to count the number of steps for the current result.
// The found paths are saved in Result. Using for save write result to writer
type Result struct {
AntsCount int
Paths []*list
}With the help of FieldInfo we understand what data we fill in for the anthill, and check the validity of the data. It was created because we read data on 1 line and use it to understand what data we are filling in.
// Modes for FieldInfo
const (
FIELD_ANTS = iota // On Reading Ants
FIELD_ROOMS // On Reading Rooms
FIELD_PATHS // On Reading Paths | Relations
)
// with fieldInfo, we understand What data we fill in for the anthill
type fieldInfo struct {
MODE byte // FIELD_ANTS | FIELD_ROOMS | FIELD_PATHS
Start, End bool // Should Be True
IsStart, IsEnd bool // For Know Which Room is Reading
UsingCoordinates map[int]map[int]bool // Chekking for unique Coordinates on Rooms
}

On Finding Optimal Path to evaluate the optimality of the path, we count the number of steps on the currently found paths. To do this, use the fastClacSteps function.
How does it work?
We can find out by the formula how many moves ants can take in one path.
Formula: KolvoMuravyev + Kolvomuravnykhkomnat On The Way
Example:
Number of Ants: 4
Start -> r1 -> r2 -> r3 -> Endr1, r2, r3 are intermediate rooms. And there are 3 of them
And it turns out according to the formula [4 + 3 = 7] all the ants will reach the End in 7 steps.
To calculate the number of steps on several paths, we do this:
We imagine that we send exactly 1 ant to each path. And according to the formula above, we get how many steps each ant takes. We save the result in a hashtable summing up the number of one-step steps.
Example:
L1 in 3 steps, L2 in 3 steps and L3 in 5 steps
And 3:2, 5:1 will be saved in the hashtable (in 3 steps 2 ants, in 5 steps 1 ant)Now finally, in order to get a number of steps for e.g. 5 ants, we start a cycle where each step receiving data from the hashtable for each step increases the loss for the ants until the ants stop.
Example of the loop:
step = 1, lossAntPerStep = 0, CountAnts = 5
step = 2, lossAntPerStep = 0, CountAnts = 5
step = 3, lossAntPerStep = 2, CountAnts = 3
step = 4, lossAntPerStep = 2, CountAnts = 1
step = 5, lossAntPerStep = 3, CountAnts = 0
Result: 5 steps.
On writing result we using any calcSteps function
// calcSteps LOGIC
func calcSteps(antsCount int, sortedPaths []*list) (int, []int) {}
// Example: PathsLens: [2, 5, 5, 6] | ants: 12
// -=-=-= Start =-=-=-
Steps = 6 = slice[slice.len-1] | (lastElem + 1) - eachElem -> [5, 2, 2, 1]
ants = ants - sumElems
DEL: [5, 2, 2, 1] | ants/slice.Len = 2/slice.len = 0.5 | ants = 2 | steps: 6+0 = 6
MOD: [6, 3, 2, 1] | ants%slice.Len = 2%4 = 2, 2-2 = 0 | ants = 0 | steps: 6+1 = 7
// On Sending Ants. x = ant
[ 1, 1, 1, 1 ] len = 0 | 12 | on st 7 = 0 | will not
[ x, 1, 1, 1 ] len = 1 | 11 | on st 6
[ x, 1, 1, 1 ] len = 1 | 10 | on st 5
[ x, 1, 1, 1 ] len = 1 | 9 | on st 4
[ x, x, x, 1 ] len = 3 | 6 | on st 3
[ x, x, x, x ] len = 4 | 2 | on st 2
[ x, x, -, - ] len = 2 | 0 | on st 1- Since we used BFS without weights, we found the path that would reach the end first. This has led to problems with cards such as:
- There was a problem with replace_edges that could not be solved
For these two reasons, we came to the conclusion that we need to change the algorithm