
This is only going to be a brief intro to OCaml, so we are not covering Data Types in this article. That will come in the next blog.
I'm trying to achieve an unconventional approach to begin the series of OCaml programming tutorials. While many tutorials typically dive into data types from the outset, I've chosen to start by discussing how OCaml is different from other languages. In this introductory phase, we'll explore fundamental aspects of the language that come into play when writing code or during compilation, such as its type inference, immutability, and expression-oriented nature.
Let's dive in!

OCaml is an objective expression-oriented programming language written in C. OCaml(Objective Caml) is an open-source, general-purpose, statically typed, functional language which is actually an extension of the Caml language with support of Object oriented programming. Sounds a lot right? Don't worry if you don't understand all of terms said above. The only key-term that can be new to everyone is the term expression-oriented. What does it signify? Let's learn that first.
All functional languages are expression oriented. In an expression oriented language, - nearly every code construct is an expression and thus yields a value.
In non-expression oriented languages we have two types of code constructs - statements & expressions where expressions must return a value that can be used elsewhere in the code while, statements generally perform actions that do not return a value. But any statement that returns a value is already qualified to be an expression.
The best example of a non-expression oriented language is C. Examples can help understand better -
/* Statements */int x = 10; // Assignment statementif (x > 4) { // Conditional Statement x = 4;}for (int i = 0; i < 5; i++) { // Loop constructs are also statements printf("%d\n", i);}/* abs() is a standard library function in C that computes the absolute value of an integer */abs(-5); // function calls are also statements /* Expressions */int sum = x + y;/* Here `x+y` is an expression that evaluates to a value that is assigned to a variable `sum` */int max = (x > y) ? x : y;/* Ternary operator( ?: ) is form of a conditional statement converted into an expression */int result = abs(-5) + 5; // This is an initialization expressionIn the above examples, int x = 10; and int result = abs(-5) + 5; are examples of both declaration statements & initialization expression.
Also, function calls are both expressions & statements because they are complete instructions that perform actions in the program but also return a value (if the return type of the function is not void).
So basically -
| Statement | Expression |
| Statements can only be declared. | Expressions can be assigned or used as operands. |
| Statements create side effects to be useful. | Expressions are values or execute to values. |
| Statements are two-sided in case of execution (they may be executed or not depending on the situation). | Expressions are unique in meaning ( because they always evaluate to a value & values are unique). |
As in an expression oriented language every statement is an expression, every piece of code returns some value.
An immutable value is a value whose state cannot be modified after it is created.
Although OCaml is not a purely functional language like HASKELL(because OCaml provides loops to use where necessary which shouldn't be in a purely functional language), OCaml strongly follows functional programming paradigm which encourages immutable data structures and values. Expressions, by their nature, are immutablethey compute values without modifying state. Mutation of states are seen as side-effects.
However it's worth noting that printing some value to the screen is also regarded as a side-effect! 😑

The good thing about immutability is it ensures data consistency by preventing unintended changes, reducing bugs caused by side effects.
Values are immutable entities representing any data in OCaml.
Unlike variables in imperative languages (like - C, Java, Python), which can change their contents over time, values in functional languages remain constant once defined.
let x = 55;; (* declaring x as an integer value of 55 *)x = 0;; (* Trying to assign 0 to x will not work. This expression will actualy check structural equality between the value of x and 0, which will evaluate to false.The `=` operator checks structural equality and `==` checks physical equality.We will cover these in upcoming articles *)(* Then what will this expression below do? *)let x = 10;;(* Trying the below code will print 10 to the screen *)print_int x;;Let's try to understand what exactly happened when we redeclared x as 10. As I said before - "values are immutable". So, it isn't any mutable assignment. It seems so because of the so called 'Shadow Effect'.
For now just know that every let binding binds a new value to a variable. Even if an old variable was declared before with the same name, the new one will shadow the former one with the same name. The old variable will still exist but remain inaccessible.
As shown in the previous examples, we declare variables in OCaml with the let keyword, without explicitly specifying the type of the value. But this does NOT necessarily signify that OCaml is dynamically typed.
Many people consider that OCaml is weakly typed. Which is not true. Although implicitly typed, the compiler comes with built-in type checker that helps ensure type safety in your code; which is an essential component of OCaml's static type system. This explains that this language is a strongly typed language.
Type inference in OCaml is a compile-time process where the type checker determines bindings' types before execution.
let name = "Debajyati";; (* The OCaml compiler will automatically inferthe type of the variable `name` as string *)The type checker infers types, making OCaml statically typed, though type annotations are supported.
let name:string = "Debajyati";; (* Type Annotations are also supported *)In functional programming, recursive functions are preferred over loops for most tasks. Recursive functions are more idiomatic in OCaml and can lead to more concise and readable code. Yes, it's true.
This section is for those who are already familiar with the concept of recursion. Recursion is nothing but a function calling itself from its definition. e.g. -
(* This is a recursive function *)let rec factorial n = if n = 0 then 1 else n * factorial (n-1);;(* Recursive functions are defined with the `rec` keyword after the `let` keyword. *)If you want to know more about functions & recursions in OCaml stay tuned for my upcoming articles. : )
Recursion in OCaml promotes concise code by encapsulating repetitive patterns. It perfectly aligns with functional programming principles, holding immutable data.
Recursion approach can cause problems if not handled efficiently. Most programming languages implement function calls with a stack. This is called the call stack.
The size of the stack is usually limited by the operating system. Call Stack contains one element for each function call that has been started but not yet completed.
In order to perform all necessary computations without reaching a Stack overflow, - like all other functional languages, OCaml has a solution called the Tail Recursion or ( a more fancy term Tail-Call Optimization.
We will learn about this approach in detail in the upcoming blogs.
I hope this introductory article sparked some interest or added some value to your time! Let me know in the comments. We will be covering data types next and more to come in future.
Until then follow me and please share this blog with your friends. :)

Have a great day ahead & most importantly -
Happy Coding! 🧑🏻💻 👩🏻💻
]]> diff --git a/data/planet/debajyatidey/build-a-cli-in-ocaml-with-the-cmdliner-library.md b/data/planet/debajyatidey/build-a-cli-in-ocaml-with-the-cmdliner-library.md new file mode 100644 index 0000000000..decfc24834 --- /dev/null +++ b/data/planet/debajyatidey/build-a-cli-in-ocaml-with-the-cmdliner-library.md @@ -0,0 +1,13 @@ +--- +title: Build A CLI in OCaml with the Cmdliner Library +description: Learn to build a command-line interface in OCaml using Cmdliner library. + Follow steps to set up, write code, and execute your CLI tool +url: https://debajyatidey.hashnode.dev/build-a-cli-in-ocaml-with-the-cmdliner-library +date: 2024-12-27T15:31:54-00:00 +preview_image: https://hashnode.com/utility/r?url=https%3A%2F%2Fcdn.hashnode.com%2Fres%2Fhashnode%2Fimage%2Fupload%2Fv1735313191864%2Fc16e8a16-8804-4645-9136-7670ed8ca5f7.gif%3Fw%3D1200%26h%3D630%26fit%3Dcrop%26crop%3Dentropy%26auto%3Dformat%2Ccompress%26gif-q%3D60%26format%3Dwebm%26fm%3Dpng +authors: +- Debajyati's OCaml Blog +source: +--- + +In this tutorial we are building a simple CLI named textsearch which is able to search a provided piece of string (probably a word) in a given text file.Prior knowledge of components of a dune project is recommended but not required. I will guide you setting up the dune project.
Entire source code of this demo project is available at - Release v0.2.1 Debajyati/textsearch
This tutorial assumes you have dune preinstalled. If not, then install it via opam -
opam install duneIn this tutorial, you'll learn to build a simple command-line interface (CLI) tool called "textsearch" using OCaml and the Cmdliner library. The tool searches for a specified term in a text file with options for case sensitivity and character order. You'll be guided through setting up a Dune project, configuring the necessary files, writing the search logic, and defining command-line arguments using Cmdliner. The tutorial covers the project structure, dependencies, and detailed explanations of the code components to help you understand and implement the CLI tool effectively.
Cmdliner is a library that helps you build command line interface programs in OCaml.
It provides a simple and compositional mechanism to create commands and arguments in a declarative syntax.
So, lets get started!

Lets start writing code. But before that we need to create a dune project.
Initialize the dune project by -
dune init proj textsearchWe will need the Cmdliner library installed in our system to build and run our project. So, install it via opam.
opam install cmdlinerGreat! Now before you write the actual code, you need to setup the dune project by writing the configuration files properly.
At the end of this tutorial the file tree of our project will be like -
. bin dune main.ml lib dune search.ml test dune test_textsearch.ml dune-project textsearch.opamHere the textsearch.opam file is not your concern, dont touch it. This file is generated by dune, edit dune-project instead.
The dune-project file defines project-wide settings.
For now, you dont need to edit most of the parts of the file dune-project.
Currently the file must look like -
(lang dune 3.17)(name textsearch)(generate_opam_files true)(source (github username/reponame))(authors "Author Name <author@example.com>")(maintainers "Maintainer Name <maintainer@example.com>")(license LICENSE)(documentation https://url/to/documentation)(package (name textsearch) (synopsis "A short synopsis") (description "A longer description") (depends ocaml) (tags ("add topics" "to describe" your project))); See the complete stanza docs at https://dune.readthedocs.io/en/stable/reference/dune-project/index.htmlNow change the package stanza to this -
(package (name textsearch) (synopsis "A simple text search CLI tool") (description "CLI tool to search terms in files") (depends (ocaml (>= 5.2)) (cmdliner (>= 1.3.0)) (dune (>= 3.17))) (tags ("cmdline" "text" "search")))Nice!
We have two important directories here -
lib/ - Holds the source code for libraries within your project.
bin/ - Contains the source code for executables.
Forget the test folder for now as we are not going to write test cases for our project (At least not in this tutorial).
We also have a dune file in each of the folders. These files define how to build the specific executable within that directory.
Specifically, they are for -
Specifying dependencies (both internal and external libraries).
Specifying rules for building the target.
Paste the following code in bin/dune file -
(executable (public_name textsearch) (name main) (libraries search cmdliner))Paste the code below in the lib/dune file -
(library (name search) (public_name textsearch))All good! Finally, the configuration work is DONE! HUH!
We can finally write the actual code.
We will need an internal library called search.ml as we have specified in the dune files. Create that file in the lib/ directory.
touch lib/search.mlNow, paste this code in the file -
let search_in_file ~case_sensitive ~consider_order term file = let normalize s = if case_sensitive then s else String.lowercase_ascii s in let term = normalize term in let contains_term line = let line = normalize line in if consider_order then try let line_len = String.length line in let term_len = String.length term in let rec check_substring i = if i + term_len > line_len then false else if String.sub line i term_len = term then true else check_substring (i + 1) in check_substring 0 with _ -> false else let term_chars = String.to_seq term |> List.of_seq in let line_chars = String.to_seq line |> List.of_seq in List.for_all (fun c -> List.mem c line_chars) term_chars in let ic = open_in file in let rec process_lines line_num acc = try let line = input_line ic in let new_acc = if contains_term line then (line_num, line) :: acc else acc in process_lines (line_num + 1) new_acc with End_of_file -> close_in ic; List.rev acc in process_lines 1 [];;let print_matches matches = List.iter (fun (line_num, line) -> Printf.printf "%d: %s\n" line_num line) matches;;Weve two functions in this file.
search_in_file - This function takes four arguments:
case_sensitive: A boolean value indicating whether the search should be case sensitive or not.
consider_order: A boolean value indicating whether the order of characters in the term matters during the search.
term: The string to search for in the file.
file: The path to the file to search in.
The function opens a file for reading. Then it recursively iterates over the lines of the file. On each iteration, the function reads a line, checks if the line contains the term. If the line contains the term, it adds the line number and the line itself as a tuple to an accumulator list. It recursively calls itself on the next line number and the updated accumulator list. When it reaches the end of the file (End_of_file exception), it closes the file and reverses the accumulated list (to display lines in their original order).
print_matches - This function takes a list of matches as input where each match is a tuple containing the line number and the line itself. It iterates over the list of matches and prints each match in the format "line_num: line".
I hope this explanation is clear and good to go ahead.
This is our bin/main.ml file. Here we will import both of our internal library Search and external library Cmdliner, and then define the command and arguments.
open Cmdlineropen Search(* Define arguments *)let search_term = let doc = "The term to search for" in Arg.(required & pos 0 (some string) None & info [] ~docv:"TERM" ~doc)let file_name = let doc = "The file to search in" in Arg.(required & pos 1 (some string) None & info [] ~docv:"FILE" ~doc)let case_sensitive = let doc = "Perform a case-sensitive search" in Arg.(value & flag & info ["c"; "case-sensitive"] ~doc)let consider_order = let doc = "Consider the order of characters in the search term" in Arg.(value & flag & info ["o"; "consider-order"] ~doc)(* Core command logic *)let run case_sensitive consider_order term file = let matches = search_in_file ~case_sensitive ~consider_order term file in print_matches matches; if List.length matches = 0 then (Printf.eprintf "No matches found.\n"; exit 1) else exit 0(* Create the command *)let cmd = let info = Cmd.info "textsearch" ~version:"1.0.0" ~doc:"Search for a term in a file with options for case sensitivity and character order" in Cmd.v info Term.(const run $ case_sensitive $ consider_order $ search_term $ file_name)(* Main entry point *)let () = Stdlib.exit (Cmd.eval cmd)Lets break down the bin/main.ml file to understand its components and the utilities of the Cmdline library used here.
After imports, we first define all the arguments as variables. The arguments for our program are defined using Cmdliner.Arg module.
In this program we defined 4 arguments.
search_term (positional argument): - The term (word) to search for in the file.
file_name (positional argument): - The file in which the term is to be searched.
consider_order (flag): - Ensures that the order of characters in the search term is considered.
case_sensitive (flag): - Enables case-sensitive search.
Explanation of the Cmdliner library utilities used here: -
Arg: This module provides functions for defining command-line arguments, including their types, descriptions, and help messages.
Arg.required: This function defines a required argument (makes the argument mandatory).
Arg.pos: This function specifies the position of an argument in the command-line syntax. So, for example, pos 0 will make the argument the first positional argument.
Arg.info: This function provides a docstring and other metadata for an argument.
Arg.value: This function defines the value of an argument. The documentation says, - (value a) is a term that evaluates to a's value.
Arg.flag: This function defines a flag argument that may appear at most once on the command line. The argument holds true if the flag is present on the command line and false otherwise.
Arg.some: This function wraps the argument value in an Option type.
Arg.(&): This is an infix operator which performs a right associative composition operation, which simply means Arg.(&) enables composition of the combinators of a command-line argument by connecting individual components (arguments type, default value, parsing logic and docs) in a declarative way.
After imports we defined the core command logic. The whole command logic is encapsulated in the run function.
The run function calls the search_in_file function from the Search library. Prints the matching lines using print_matches function. Exits with code 1 if no matches are found, else exit code 0.
Next, we define the command in the cmd variable.
And finally, there is the main entry point of our program where it starts its execution from. That is -
let () = Stdlib.exit (Cmd.eval cmd)Here, the cmd command gets evaluated and then exits the program with the return code from run.
Explanation of all the Cmdliner library utilities used here: -
Cmd: This module is the core of Cmdliner. It provides functions to define the commands, specify their options and arguments, and handle argument parsing, grouping and usage messages.
Cmd.info: This function creates a command description, including its name, version, and helptexts (a docstring explaining its purpose).
Cmd.v: This function creates a fully functional command combining the provided info and terms.
Cmd.eval: This function evaluates the given command, parses arguments, and executes the corresponding logic.
Term: This module deals with creating and manipulating command-line terms (arguments and subcommands).
Term.const: This function creates a term that evaluates to a constant value. In the given code, it's used to create terms for the run function and its arguments.
Term.($) - An infix operator that combines terms to pass arguments to a function (eventually the command to run from terminal).
So, you finally understood the Cmdline library.
Now its time to build and run our project to see if this works or not.
Without waiting, let's build and run it!
Open your terminal and navigate to the root directory of your project (where dune-project is located).
Run the following command to build the program:
dune buildThis command will use the dune files to compile the source code in lib/search.ml and bin/main.ml and create an executable named textsearch in the _build/install/default/bin/ directory.
Now, you can run the executable by this command -
dune exec -- textsearch -c -o <term> "path/to/file/to/search/in"Here, <term> is the term you want to search in the file.
Replace "path/to/file/to/search/in" with the actual path of the file you want to search the term in.
-c is the optional flag for case-sensitivity,
-o is the optional flag for respecting order of characters.
For example, I use vim and have the vim config file .vimrc located in the $HOME directory of my system.
I want to search my name in the file if its there. I would run -
dune exec -- textsearch -c -o Debajyati ~/.vimrcAnd the program would print the matching lines in the console.

Tadaaa! And it works pretty well and smooth! Neat!
Congratulations! 🎉 You now have a functional CLI tool built with OCaml and Cmdliner!
I would really appreciate your feedback on this tutorial. How would you rate it? How can I improve it?
If you found this project or tutorial helpful, please consider starring the repository below. It will encourage me to create more content like this.
If you found this POST helpful, if this blog added some value to your time and energy, please show some love by giving the article some likes and share it with your developer friends.
Feel free to connect with me at - Twitter, LinkedIn or GitHub :)
Happy Coding 🧑🏽💻👩🏽💻! Have a nice day ahead! 🚀
]]> diff --git a/data/planet/debajyatidey/data-types-in-ocaml.md b/data/planet/debajyatidey/data-types-in-ocaml.md new file mode 100644 index 0000000000..d4194a9a95 --- /dev/null +++ b/data/planet/debajyatidey/data-types-in-ocaml.md @@ -0,0 +1,13 @@ +--- +title: Data Types in OCaml +description: Learn OCaml's diverse data types in functional programming, their features, + and efficient usage in code. +url: https://debajyatidey.hashnode.dev/data-types-in-ocaml +date: 2024-02-27T17:35:36-00:00 +preview_image: https://hashnode.com/utility/r?url=https%3A%2F%2Fcdn.hashnode.com%2Fres%2Fhashnode%2Fimage%2Fupload%2Fv1709055320479%2Fbc3047da-295e-47db-9005-56a2071159c6.gif%3Fw%3D1200%26auto%3Dformat%2Ccompress%26gif-q%3D60%26format%3Dwebm%26fm%3Dpng +authors: +- Debajyati's OCaml Blog +source: +--- + +IntroductionIn the previous article we discussed about how OCaml is different than other languages, its expression oriented nature, its static type system & some other aspects.
In this article we will mainly discuss about the data-types in this language.
But before we directly head on to the main topic, let me share some insights about the tools we will be using.
Utop(Universal Top-Level for OCaml) is similar to IPython3 for python with some different features.
Although you can manually install utop with the default package manager apt(assuming you are using ubuntu,. If you have windows computer, use WSL2 instead). I recommend you to follow each and every step described in the webpage(link below) to install opam, OCaml, and setup an opam switch (similar to virtual environments of python3).
Click here to see the steps. It may seem time consuming, but trust me it's worth it.
now once you have installed & set up ocaml, opam and utop, you must know how to run an existing ocaml file.
Run without compiling:
If you're not using any other library rather than the standard library, you can then only run without compiling the code. To do that -
ocaml filename.ml #place the appropriate path to the ocaml file in place of `filename.ml`Compiling and running:
The compiler we use to compile and run ocaml programs is ocamlc. The compiler first compiles the source file into byte code then we manually run the binary byte file.
ocamlc -o filename.byte filename.ml./filename.byteIf you observe enough you'll see, two more files are also generated, filename.cmo and filename.cmi. These are not used in running code. These are for different purposes. We don't need them now. So clean them using -
rm filename.cmi filename.cmo
NOTE: We can write multiline comments in OCaml inside
(* *)- this syntax.e.g. -
(* This is a comment *)
Enter utop in the terminal and get ready to write code.
You should see a similar looking interface after running utop(img above).
;; (double semicolon). Whenever you'll evaluate an expression in utop, it will show the resulting value and type in the next one or few lines.The primitive types are unit, int, char, float, bool, and string.
The unit type is the simplest type in OCaml. It contains one element: ( ). Seems stupid, right? Actually not!
In an expression oriented language, every expression must return a value. Then what about those expressions which perform side effects?
( ) is used as the value of a procedure that makes any side-effect. It is similar to the void data type in C.
print_endline "Let's Learn OCaml";;(* This expression prints the specified string to the screen. Printing something to screen is seen as a side-effect. So, this expression will return a unit. *)This is the type of signed Integers. All positive integers(1,2,3,4, ...), all negative integers(... ,-4,-3,-2,-1) and 0 are recognised as integers.
OCaml integers range from -
$$-2^{62}\ \ to\ \ 2^{62} - 1$$
on modern computer systems.
let num = 5;; (* integer expression *)val num : int = 5 (* utop output *)int described in binary - starts with 0b
int described in octal - starts with 0o
int described in hexadecimal - starts with 0x
The syntax of a floating point requires a decimal point, an exponent (base 10) denoted by an E or e. A digit is required before the decimal point, but not after. Let's look at some examples -
31.415926E-1;; (* float value *)- : float = 3.1415926 (* utop output *)let number = 2e7;; (* float expression *)val number : float = 20000000. (* utop output *)(* float expression with unnecessary type annotation*)let floating:float = 0.01;;val floating : float = 0.01 (* utop output *)The expression type char belongs to the ASCII character set. The syntax for a character constant uses the single quote symbol. e.g. - 'a', 'x', 'F', ' ' etc.
But there's more to know! Escape Sequences though commonly associated with strings, they're also expressed as char.
Must Know Escape Sequences:
| Sequences | Definition |
'\\' | The backslash character |
'\'' | The single-quote character |
'\t' | The tab character |
'\r' | The carriage-return character |
'\n' | The newline character |
'\ddd' | The decimal escape sequence |
A decimal escape sequence must have exactly three decimal characters. It specifies the ASCII character with the given decimal code.
Let's see some examples -
let ch = 'x';; (* char expression *)val ch : char = 'x' (* utop output *)'\123';; (* decimal escape sequence value *)- : char = '{' (* utop output *)'\121';; (* decimal escape sequence value *)- : char = 'y' (* utop output *)In OCaml, strings are a primitive type represented by character sequences delimited by double quotes. Unlike C, OCaml strings are not arrays of characters and do not employ the null-character '\000' for termination. Strings in OCaml support escape sequences for specifying special characters, akin to those used for individual characters.
let str = "Hello\n World!";; (* string expression *)val str : string = "Hello\n World!" (* utop output *)(* The Absolute Nightmare way to write an helloworld program *)let greet = "\072\101\108\108\111\044 \087\111\114\108\100\033";;val greet : string = "Hello, World!"The bool type includes true and false, and logical negation is done via the not function. Comparison operations (=, ==, !=, <>, <, <=, >=, >) return true if the relation holds; == is used for checking physical equality, while = implies structural equality.
| Boolean Expression | What does it signify |
| x = y | x is equal to y |
| x <> y | x is not equal to y |
| x == y | x is "identical" to y |
| x != y | x is not "identical" to y |
| x > y | x is strictly greater than y |
| x >= y | x is greater than or equal to y |
| x < y | x is strictly less than y |
| x <= y | x is less than or equal to y |
If you're someone experienced in python, java or C++, you have to practice using = in conditions, instead of ==.
5.1 = 5.1;; (* boolean expression checking structural equality *)- : bool = true (* utop output *)5.1 != 5.1;; (* boolean expression checking physical inequality *)- : bool = true (* utop output *)OCaml provides some functions to convert some primitive types to another.
use - int_of_string
int_of_string "145";;- : int = 145use - int_of_char
int_of_char 'o';;- : int = 111use - int_of_float
int_of_float 1.9999999;; (* returns the floor value of the float *)- : int = 1use - Char.code
Char.code 'd';; (* Char is a module which has a function named `code` to do this *)- : int = 100use - float_of_int
float_of_int 52;;- : float = 52.0use - float_of_string
float_of_string "5";;- : float = 5.float_of_string "0.5";;- : float = 0.5use - char_of_int
char_of_int 55;;- : char = '7'char_of_int 97;;- : char = 'a'char_of_int 67;;- : char = 'C'use - Char.chr
Char.chr 45;;- : char = '-'Char.chr 105;;- : char = 'i'use - string_of_int
string_of_int 746;;- : string = "746"use - string_of_bool
string_of_bool true;;- : string = "true"use - string_of_float
string_of_float 45.0;;- : string = "45."use - bool_of_string
let wrong = bool_of_string "false";;val wrong : bool = false(* `bool_of_string` only works if the provided string is "false" or "true" *)bool_of_string "";;Exception: Invalid_argument "bool_of_string". (* throwing an exception/error *)We can define custom data types using a type definition with the type keyword. These are also called variants.
Example -
(* Defining a type representing different days of the week *)type day = | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday;;(* `|` is a symbol in OCaml that seperates different patterns or cases. It is mainly used in type definitions and pattern matching code.*)(* utop output *)type day = Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | SundayLists are homogeneous collections represented by square brackets. They are immutable and support powerful pattern matching operations, making them essential in functional programming.
(* Defining a list of integers *)let numbers = [1; 2; 3; 4; 5];; val numbers : int list = [1; 2; 3; 4; 5]Arrays in OCaml, denoted by the array keyword, are fixed-size collections of elements of the same data type. They are zero-indexed and can be accessed using square brackets.
let numbers = [|1; 2; 3|];; (* defining an array of integers *)val numbers : int array = [|1; 2; 3|] (* utop output *)Tuples are ordered collections of elements of different types. They offer a convenient way to group heterogeneous data. A parenthetical space () separates the tuple's components from one another.
(* Defining a tuple *)let credentials = ("Debajyati", 6);;val credentials : string * int = ("Debajyati", 6) (* utop output *)(* matching the pattern to access individual elements *)let (name, roll) = credentials;;val name : string = "Debajyati" (* utop output *)val roll : int = 6(* printing a string with those values *)Printf.printf "Roll no. of %s is %d\n" name roll;;Roll no. of Debajyati is 6 (* utop output *)- : unit = ()Records are labeled collections of fields, akin to structs in other languages. They allow for structured data representation and manipulation.
(* Defining a record representing a person *)type person = { name : string; age : int;};;type person = { name : string; age : int; } (* utop output *)(* Creating a person record *)let john = { name = "John"; age = 30 };;val john : person = {name = "John"; age = 30} (* utop output *)(* Accessing fields of the record *)let () = Printf.printf "%s is %d years old\n" john.name john.age;;John is 30 years old (* utop output *)Algebraic data types in OCaml are a way of defining composite types by combining simpler types using constructors, through variant types and recursive types, respectively.
Variant types enable the creation of sum types, where a value can be one of several possibilities. They are particularly useful for modeling complex data structures and handling multiple cases in pattern matching. We already saw an example of Variant Types in OCaml in the Custom types section of this blog. Let's see another example -
(* Defining a variant type representing shapes *)type shape = | Circle of float | Rectangle of float * float;;type shape = Circle of float | Rectangle of float * float (* utop output *)(* Creating instances of shapes *)let circle = Circle 5.0;;val circle : shape = Circle 5. (* utop output *)let rectangle = Rectangle (3.0, 4.0);;val rectangle : shape = Rectangle (3., 4.) (* utop output *)Recursive variant types allow for the definition of recursive data structures, such as linked lists and binary trees. One basic example using linked lists -
(* Defining a recursive list type *)type 'a mylist = | Empty | Cons of 'a * 'a mylist;;type 'a mylist = Empty | Cons of 'a * 'a mylist (* utop output *)(* Creating a list of integers *)let rec int_list = Cons (1, Cons (2, Cons (3, Empty)));;val int_list : int mylist = Cons (1, Cons (2, Cons (3, Empty))) (*utop output*)'a represents a type variable, indicating that the type of elements in the tree can be any type. It's a placeholder for a concrete type that will be specified when the tree is instantiated.Empty represents the end of a list, indicating that there are no more elements left. Cons represents adding an element to the front of a list, combining the new element with the rest of the list.The option data type, denoted by the 'option' keyword, is used to represent values that may or may not be present. It is particularly useful for handling null or undefined values.
Example:
let maybe_number: int option = Some 42;;val maybe_number : int option = Some 42 (* utop output *)Wait, there exists such things like a Module Type?? Wow! 🫡

In OCaml, modules provide a way to encapsulate related code, data, and types. They serve as containers for organizing and structuring code, much like namespaces in other languages. Module types, then, define the interface or signature of a module, specifying the types and functions that must be implemented by any module that conforms to it.
Module types play a crucial role in enforcing abstraction and modularity in OCaml programs. By defining interfaces through module types, developers can separate the concerns of implementation details from the external interface.
To define a module type, we use the module type keyword followed by a name and a set of specifications. These specifications include the types and functions that the module must provide. For instance, consider a module type defining the interface for a stack data structure:
module type StackType = sig type 'a t val empty : 'a t val push : 'a -> 'a t -> 'a t val pop : 'a t -> 'a option * 'a tend;;(* utop output - same actually 🥲 *)module type StackType = sig type 'a t val empty : 'a t val push : 'a -> 'a t -> 'a t val pop : 'a t -> 'a option * 'a t endHere, StackType is a module type specifying that any module implementing it must define a type 'a t representing a stack, as well as functions empty, push, and pop for stack manipulation.
Once a module type is defined, we can create modules that adhere to it by providing concrete implementations for its specifications. For example, we can implement the Stack module type as follows:
module Stack : StackType = struct type 'a t = 'a list (* Instantiating the variant type *) let empty = [] let push x s = x :: s (* pattern matching expression used to define an expression *) let pop = function | [] -> (None, []) | x :: xs -> (Some x, xs) (* `::` is the Cons operator *)end;;module Stack : StackType (* utop output *)So, finally we are done. Now you know all the most important and noteworthy data types in OCaml.
Mastering data types in OCaml is essential for writing maintainable & efficient code. From primitive types to algebraic data types and module types, OCaml has many tools for data manipulation & abstraction.
In future blog posts, we will explore advanced topics such as recursion, higher-order functions, and OCaml's module system. Stay tuned!
Until then you can connect with me on twitter :) & share this article with your friends!

Most importantly, - Happy Coding! 🧑🏻💻 👩🏻💻
]]> diff --git a/data/planet/debajyatidey/functions--solving-problems-in-ocaml.md b/data/planet/debajyatidey/functions--solving-problems-in-ocaml.md new file mode 100644 index 0000000000..690bb4dbd7 --- /dev/null +++ b/data/planet/debajyatidey/functions--solving-problems-in-ocaml.md @@ -0,0 +1,12 @@ +--- +title: Functions & Solving Problems in OCaml +description: Getting Started with writing Functions & Problem-Solving in OCaml +url: https://debajyatidey.hashnode.dev/functions-solving-problems-in-ocaml +date: 2024-03-06T18:16:06-00:00 +preview_image: https://hashnode.com/utility/r?url=https%3A%2F%2Fcdn.hashnode.com%2Fres%2Fhashnode%2Fimage%2Fupload%2Fv1709749162345%2F947f7089-3934-48e8-b204-7a056ff10c7f.gif%3Fw%3D1200%26auto%3Dformat%2Ccompress%26gif-q%3D60%26format%3Dwebm%26fm%3Dpng +authors: +- Debajyati's OCaml Blog +source: +--- + +In one of the previous articles, we've seen how to define a basic function with if-else expressions. In this article, we are going to get through the detailed overview of defining efficient functions and developing intuition to solve problems in the way of functional programming.If you already haven't read my previous blogs in this series, I strongly recommend you go and give them a read. Those will help you get a structured idea of how things are different and how expressions work in OCaml.
Without wasting time Let's open utop & directly head towards the topic.

See below - a normal function definition.
let is_positive n = if n > 0 then true else false;;(* In OCaml, function definitions don't contain any return statement. While in many imperative languages like - C, Java, C++, they do *)val is_positive : int -> bool = <fun> (* utop output *)else statement. Without an else statement, a conditional expression will throw an error. To write more than two conditions, add the middle one with else if. We don't do elif here just as we do in python.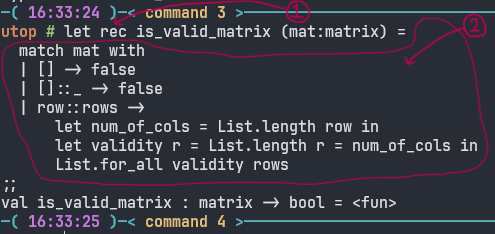
You can see above there is an example of a recursive function in OCaml. From the image, we understand -
Recursive functions are defined with adding a rec keyword just after the let keyword.
Let it be recursive or any normal function, the whole chunk of code at the right-hand side of the = (equal) sign, always is an expression. Whatever this expression evaluates is the return value. Hence, no return statement required.
There are always consequences of your decisions...
The syntax for calling any function in OCaml is entirely different from your experience in some imperative or multi-paradigm languages, such as - Java, Python, JavaScript, C++, etc.
# Defining a function in pythondef is_positive(x): # argument `x` inside parenthesis `()` if x > 0: return True # return statement else: return False # return statement# Calling itis_positive(20)In those languages, you place parenthesis after the function name and pass arguments inside that parenthesis. We don't do that here in OCaml. Here, all arguments are passed one after the another based on the sequence or labels(as defined) separated by spaces.
(* Defining a function in OCaml *)let is_negative n = if n < 0 then true else false;;val is_negative : int -> bool = <fun> (* utop output *)(* Calling it *)is_negative (-50);; (* grouping the value inside parenthesis because it contains a sign. Otherwise the compiler will misunderstand `is_negative` as an integer expression instead of a function and as a result, will throw an error. *)- : bool = true (* utop output *)Example of a function taking multiple arguments.
(* A function that computes sum of 2 integers & returns it as a string *)let string_sum (num1:int) (num2:int) = string_of_int (num1 + num2);; val string_sum : int -> int -> string = <fun> (* utop output *)The functions that take more than 1 argument, are called curried functions. What does it mean? Let's learn that first.
Currying is a technique used in functional programming to transform a function that takes multiple arguments into a sequence of functions that take one argument each. This allows you to partially apply arguments to a function, creating new functions of fewer arguments. In OCaml, you can easily implement currying using lambda expressions or by defining a separate function.
Let's consider a simple function that adds two numbers:
let add x y = x + y;;val add : int -> int -> int = <fun> (* utop output *)In this case, add is a function that takes two arguments, x and y, and returns their sum. Now, we can curry this function to create a sequence of functions that take one argument each:
let curried_add = add;;val curried_add : int -> int -> int = <fun> (* utop output *)curried_add 1;;- : int -> int = <fun> (* utop output *)let curried_add_one = curried_add 1;;val curried_add_one : int -> int = <fun> (* utop output *)curried_add 1 2;;- : int = 3 (* utop output *)(* same thing would be below *)curried_add_one 2;;- : int = 3 (* utop output *)So basically, in OCaml, each & every function takes exactly one argument.
Lambda expressions, also known as anonymous functions, are widely used in OCaml. They allow you to define functions without assigning them to a specific name.
Learn the syntax with a basic example of using lambda expressions in OCaml:
(* Non-lambda function finding square of a number *)let square x = x * x;;val square : int -> int = <fun> (* utop output *)(* Lambda Function doing the same thing *)fun x -> x * x;;- : int -> int = <fun> (* utop output *)See below a good example of a lambda expression as an argument passed to a function that takes a function as an argument.
(* map is a function defined in the List module that applies a function given as 1st argument to each of the elements of the list given as the 2nd argument & return the resulting list. *)List.map (fun x -> x * x) [1; 2; 3];;- : int list = [1; 4; 9] (* utop output *)So, what about those lambda expressions that returns something independent of any argument or frankly speaking, a lambda expression that doesn't take any arguments?
Exactly, you're thinking absolutely correct. We'll provide unit () to that function as argument.
fun () -> print_endline "I entered the void btw";; - : unit -> unit = <fun> (* utop output *)Recursion, in the context of programming, refers to a technique where a function calls itself repeatedly until a specific condition is met. This process allows you to solve complex problems by breaking them down into smaller, more manageable subproblems.
In functional programming, these subproblems are handled with small functions defined at different local scopes or some pattern matching expressions. Pattern Matching is a crucial concept in many functional programming Languages. OCaml is not any exception here. We are getting into pattern matching later.
(* Recursive Function to calculate the nth fibonacci sequence term *)let rec fib n = let rec helper n previous current = (* Implementing a tail recursion with the helper function to make the function efficient & less prone to stack overflows *) if n = 1 then current else helper (n - 1) current (previous + current) in if n > 0 then helper n 0 1 else raise (Invalid_argument "n must be greater than 0");; (* Handling Exceptions so that we don't get errors *)The above function has a helper function defined in a lower scope that can't be accessed outside of the function fib definition. This function could be written in a more efficient way. And that way would be involving match expressions.
If you're not familiar with writing useful programs in functional programming languages, you should know that every single step to solve a problem or make some meaningful program involves a function.
Just like the procedures in an object-oriented language like Java involve implementing Classes, Objects and Methods; OCaml as a functional language, involve implementation of pure functions with strong emphasis on immutability.
Although OCaml is not a purely functional language (it has loops, classes) but it still strongly supports the principles of functional programming.
Let's try to solve a problem in OCaml with some functions.
(* Write a program to calculate the sum of the integer list elements *)(* Defining the function *)let rec sum_list lst = if lst = [] then 0 (* base case *) (* List.hd takes 1st element & List.tl takes list of rest of the elements *) else List.hd lst + sum_list (List.tl lst) (* recursively calling the function *);;val sum_list : int list -> int = <fun> (* utop output *)(* Calling the function to perform the sum on the list *)Printf.printf "%d\n" (sum_list [1;4;5;6;9;9;55]);;89 (* utop *)- : unit = () (* output *)Note that this function is not implemented with a match expression. Let's first learn this and then we will solve the same problem again with pattern matching technique.
We match different patterns of an argument or its specification to handle all different possible cases of a recursive function. Let's see how that works.
In OCaml, pattern matching is typically performed using the match keyword.
(* Basic syntax of pattern matching *)match expression with| pattern1 -> expression1| pattern2 -> expression2| pattern3 -> expression3...| _ -> default_expression;;Pattern Matching in OCaml involves comparing input data against a set of predefined patterns to determine which pattern best matches the input. When a match is found, the corresponding actions or expressions are executed. Pattern matching is not limited to simple values but can also be applied to more complex data structures like tuples, lists, and even user-defined types.
(* computing factorial with match expression *)let rec factorial n = if n >= 0 then match n with | 0 -> 1 | _ -> n * factorial (n - 1) (* `_` is the wildcard character. It can be anything! *) else failwith "Only non-negative integers are supported!" (* Error Handling *);;val factorial : int -> int = <fun> (* utop output *)factorial 5;;- : int = 120 (* utop output *)factorial (-5);;Exception: Failure "Only non-negative integers are supported!". (* utop output *)We can write the same function implementing pattern matching without the match keyword. Yes! That would be the function keyword. Example will make it crystal clear.
(* Without error handling *)let rec factorial = function | 0 -> 1 | n -> n * factorial (n - 1);;val factorial : int -> int = <fun> (* utop output *)(* With Error Handling *)let rec factorial = function | 0 -> 1 | n -> if n >= 0 then n * factorial (n - 1) else failwith "Only non-negative integers are supported!";;val factorial : int -> int = <fun> (* utop output *)Tuple Patterns:
let get_first_element tuple = match tuple with | (x, _) -> x;;val get_first_element : 'a * 'b -> 'a = <fun> (* utop output *)List Patterns:
let rec sum_list lst = match lst with | [] -> 0 | head :: tail -> head + sum_list tail;;val sum_list : int list -> int = <fun> (* utop output *)Constructor Patterns (for algebraic data types):
type color = Red | Green | Blue;; (* Defining a variant type *)type color = Red | Green | Blue (* utop output *)let color_to_string c = match c with | Red -> "Red" | Green -> "Green" | Blue -> "Blue";;val color_to_string : color -> string = <fun> (* utop output *)Record Patterns:
type person = { name : string; age : int };;type person = { name : string; age : int; } (* utop output *)let is_adult (p:person) = match p with | { name = _; age = a } when a >= 18 -> true | _ -> false;;val is_adult : person -> bool = <fun> (* utop output *)Now as you know how to write patterns to handle all important cases, let's rewrite the function to calculate nth Fibonacci number using a match expression.
(* Fibonacci using pattern matching *)let fib n = let rec helper n prev curr = match n with | 0 -> prev | 1 -> curr | _ -> helper (n - 1) curr (prev + curr) in if n < 0 then raise (Invalid_argument "fibonacci: n must be a non-negative integer") else helper n 0 1;;val fib : int -> int = <fun> (* utop output *)fib 100;;- : int = 3736710778780434371 (* utop output *)You can clearly see that the above implementation of Fibonacci number generator is not any ordinary one because it itself isn't recursive. The helper function it uses is recursive. It is a highly optimized function which is less susceptible to Stack Overflows.
This approach ensures that the function can be optimized by the OCaml compiler to use constant stack space.
This is how you can implement efficient, highly performant & powerful functions by combining Pattern Matching with tail call optimization.
While pattern matching offers numerous benefits, it's essential to use it judiciously to ensure code readability and performance. Some best practices to consider include:
Use pattern matching when the structure of the data is known or can be inferred from the problem context.
Break down complex patterns into smaller, more manageable patterns to improve code readability.
Avoid using overly specific patterns that might limit the flexibility of your code.
Be mindful of performance when working with large data structures or deeply nested patterns, as pattern matching can have a higher time complexity compared to other operations, based on the situation.
I hope you enjoyed this article this far.
If this piece of content added a value to your time & energy, please consider giving some likes to this blog and share with others.

Happy Coding! 🧑🏻💻 👩🏻💻
]]>