db.json

{"meta":{"version":1,"warehouse":"4.0.0"},"models":{"Asset":[{"_id":"node_modules/hexo-theme-bamboo/source/favicon.ico","path":"favicon.ico","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/css/animate.min.css","path":"css/animate.min.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/css/style.styl","path":"css/style.styl","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/activate-power-mode.js","path":"js/activate-power-mode.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/app.js","path":"js/app.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/goTop.js","path":"js/goTop.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/jquery3.5.1.js","path":"js/jquery3.5.1.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/local_search.js","path":"js/local_search.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/ribbon.min.js","path":"js/ribbon.min.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/vue2.6.11.js","path":"js/vue2.6.11.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/wrapImage.js","path":"js/wrapImage.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/1.jpg","path":"medias/1.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/10.jpg","path":"medias/10.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/11.jpg","path":"medias/11.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/12.jpg","path":"medias/12.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/13.jpg","path":"medias/13.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/14.jpg","path":"medias/14.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/15.jpg","path":"medias/15.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/2.jpg","path":"medias/2.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/3.jpg","path":"medias/3.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/4.jpg","path":"medias/4.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/5.jpg","path":"medias/5.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/6.jpg","path":"medias/6.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/7.jpg","path":"medias/7.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/8.jpg","path":"medias/8.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/9.jpg","path":"medias/9.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/about.jpg","path":"medias/about.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/archive.jpg","path":"medias/archive.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/categories.jpg","path":"medias/categories.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/categoryDetail.jpg","path":"medias/categoryDetail.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/comment-bg.gif","path":"medias/comment-bg.gif","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/comment.jpg","path":"medias/comment.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/comment2.jpg","path":"medias/comment2.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/friend.jpg","path":"medias/friend.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/logo.png","path":"medias/logo.png","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/tag.jpg","path":"medias/tag.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/tagDetail.jpg","path":"medias/tagDetail.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/wx.jpg","path":"medias/wx.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/zfb.jpg","path":"medias/zfb.jpg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/bubble/bubble.js","path":"js/bubble/bubble.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/bubble/homeBubble.js","path":"js/bubble/homeBubble.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/aplayer/APlayer@1.10.1.min.css","path":"js/aplayer/APlayer@1.10.1.min.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/clipboard/clipboard.min.js","path":"js/clipboard/clipboard.min.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/cursor/explosion.min.js","path":"js/cursor/explosion.min.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/cursor/fireworks.js","path":"js/cursor/fireworks.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/cursor/clicklove.js","path":"js/cursor/clicklove.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/cursor/text.js","path":"js/cursor/text.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/falling/sakura.js","path":"js/falling/sakura.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/danmu/barrager.css","path":"js/danmu/barrager.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/falling/snow.js","path":"js/falling/snow.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/danmu/close.png","path":"js/danmu/close.png","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/danmu/jquery.barrager.js","path":"js/danmu/jquery.barrager.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/fancybox/jquery.fancybox.min.js","path":"js/fancybox/jquery.fancybox.min.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/fancybox/jquery.fancybox.min.css","path":"js/fancybox/jquery.fancybox.min.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/issues/index.js","path":"js/issues/index.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/loaded/index.css","path":"js/loaded/index.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/pjax@0.2.8/index.js","path":"js/pjax@0.2.8/index.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism-coy.min.css","path":"js/prism/prism-coy.min.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism-dark.min.css","path":"js/prism/prism-dark.min.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism-funky.min.css","path":"js/prism/prism-funky.min.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism-line-numbers.css","path":"js/prism/prism-line-numbers.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism-okaidia.min.css","path":"js/prism/prism-okaidia.min.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism-solarizedlight.min.css","path":"js/prism/prism-solarizedlight.min.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism-tomorrow.min.css","path":"js/prism/prism-tomorrow.min.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism-twilight.min.css","path":"js/prism/prism-twilight.min.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism.min.css","path":"js/prism/prism.min.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/shareJs/font.css","path":"js/shareJs/font.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/shareJs/share.min.css","path":"js/shareJs/share.min.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/shareJs/social-share.min.js","path":"js/shareJs/social-share.min.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/swiper/swiper.animate1.0.3.min.js","path":"js/swiper/swiper.animate1.0.3.min.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/swiper/swiper.min.js","path":"js/swiper/swiper.min.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/swiper/swiper@5.4.1.min.css","path":"js/swiper/swiper@5.4.1.min.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/swiper/vue-awesome-swiper.js","path":"js/swiper/vue-awesome-swiper.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/tocbot/tocbot.css","path":"js/tocbot/tocbot.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/tocbot/tocbot.min.js","path":"js/tocbot/tocbot.min.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/twikoo/twikoo.all.min.js","path":"js/twikoo/twikoo.all.min.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/twikoo/twikoo.all.min.js.LICENSE.txt","path":"js/twikoo/twikoo.all.min.js.LICENSE.txt","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/utils/index.js","path":"js/utils/index.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/valine/av-min@3.0.4.js","path":"js/valine/av-min@3.0.4.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/vue-seamless-scroll/index.js","path":"js/vue-seamless-scroll/index.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/vue-typed-js/index.css","path":"js/vue-typed-js/index.css","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/vue-typed-js/index.js","path":"js/vue-typed-js/index.js","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/medias/cursor/Horizontal.cur","path":"medias/cursor/Horizontal.cur","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/shareJs/fonts/iconfont.ttf","path":"js/shareJs/fonts/iconfont.ttf","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/shareJs/fonts/iconfont.svg","path":"js/shareJs/fonts/iconfont.svg","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/shareJs/fonts/iconfont.eot","path":"js/shareJs/fonts/iconfont.eot","modified":0,"renderable":1},{"_id":"node_modules/hexo-theme-bamboo/source/js/shareJs/fonts/iconfont.woff","path":"js/shareJs/fonts/iconfont.woff","modified":0,"renderable":1},{"_id":"source/062202062582_0logo.ico","path":"062202062582_0logo.ico","modified":0,"renderable":0},{"_id":"source/medias/1.jpg","path":"medias/1.jpg","modified":0,"renderable":0},{"_id":"source/medias/10.jpg","path":"medias/10.jpg","modified":0,"renderable":0},{"_id":"source/medias/11.jpg","path":"medias/11.jpg","modified":0,"renderable":0},{"_id":"source/medias/12.jpg","path":"medias/12.jpg","modified":0,"renderable":0},{"_id":"source/medias/13.jpg","path":"medias/13.jpg","modified":0,"renderable":0},{"_id":"source/medias/14.jpg","path":"medias/14.jpg","modified":0,"renderable":0},{"_id":"source/medias/15.jpg","path":"medias/15.jpg","modified":0,"renderable":0},{"_id":"source/medias/2.jpg","path":"medias/2.jpg","modified":0,"renderable":0},{"_id":"source/medias/3.jpg","path":"medias/3.jpg","modified":0,"renderable":0},{"_id":"source/medias/4.jpg","path":"medias/4.jpg","modified":0,"renderable":0},{"_id":"source/medias/5.jpg","path":"medias/5.jpg","modified":0,"renderable":0},{"_id":"source/medias/6.jpg","path":"medias/6.jpg","modified":0,"renderable":0},{"_id":"source/medias/7.jpg","path":"medias/7.jpg","modified":0,"renderable":0},{"_id":"source/medias/8.jpg","path":"medias/8.jpg","modified":0,"renderable":0},{"_id":"source/medias/9.jpg","path":"medias/9.jpg","modified":0,"renderable":0},{"_id":"source/medias/about.jpg","path":"medias/about.jpg","modified":0,"renderable":0},{"_id":"source/medias/archive.jpg","path":"medias/archive.jpg","modified":0,"renderable":0},{"_id":"source/medias/categories.jpg","path":"medias/categories.jpg","modified":0,"renderable":0},{"_id":"source/medias/categoryDetail.jpg","path":"medias/categoryDetail.jpg","modified":0,"renderable":0},{"_id":"source/medias/comment-bg.gif","path":"medias/comment-bg.gif","modified":0,"renderable":0},{"_id":"source/medias/comment.jpg","path":"medias/comment.jpg","modified":0,"renderable":0},{"_id":"source/medias/comment2.jpg","path":"medias/comment2.jpg","modified":0,"renderable":0},{"_id":"source/medias/friend.jpg","path":"medias/friend.jpg","modified":0,"renderable":0},{"_id":"source/medias/logo.png","path":"medias/logo.png","modified":0,"renderable":0},{"_id":"source/medias/tag.jpg","path":"medias/tag.jpg","modified":0,"renderable":0},{"_id":"source/medias/tagDetail.jpg","path":"medias/tagDetail.jpg","modified":0,"renderable":0},{"_id":"source/medias/wx.jpg","path":"medias/wx.jpg","modified":0,"renderable":0},{"_id":"source/medias/zfb.jpg","path":"medias/zfb.jpg","modified":0,"renderable":0},{"_id":"source/medias/images/QUI.gif","path":"medias/images/QUI.gif","modified":0,"renderable":0}],"Cache":[{"_id":"source/.DS_Store","hash":"9b3ea14792cd8580a7ed0ba154636b07d41d8abb","modified":1643438588041},{"_id":"source/_posts/.DS_Store","hash":"792fe8cb49aea9582c6c0ad0172924bbc066d8fc","modified":1643375978596},{"_id":"source/062202062582_0logo.ico","hash":"a84dd50428df3cdf4da641f47255323776734bf1","modified":1643375702938},{"_id":"source/_posts/读书大本营.md","hash":"3f221264f3a52bc497cf13431204b3abde379e15","modified":1643375702941},{"_id":"source/bizhi/index.md","hash":"0b63c021a92340df741f3682dc2ed338d4eec339","modified":1643438589029},{"_id":"source/about/index.md","hash":"2188230b3d55ed387a31332b75316cbb2d293d21","modified":1643438263820},{"_id":"source/medias/2.jpg","hash":"bc25752d286c7638b2c82eae897c3bbfd1281f51","modified":1643375702949},{"_id":"source/medias/5.jpg","hash":"b40c58fa6ceaa48ea139b0ef96ba1d7a9ab2b618","modified":1643375702953},{"_id":"source/medias/comment.jpg","hash":"d0e27cf8623d6bf743b5d099dfc2916bcab4e4d7","modified":1643375702962},{"_id":"source/medias/logo.png","hash":"7a6561cc59bceb362ce62c4a4e2c45d1144267dd","modified":1643375703114},{"_id":"source/gallery/index.md","hash":"4103efc86bf5ab9277b15eaeddd8d73a21dba929","modified":1643438179654},{"_id":"source/tags/index.md","hash":"996b53c94e6f7a55b6dd1fd33cc069d625683083","modified":1643438318586},{"_id":"source/friends/index.md","hash":"25272470384d937ae1ac0639962a999e6bbcba2f","modified":1643438246330},{"_id":"source/categories/index.md","hash":"31e7086bbe0dbe784fb108865e46d505e109c1e1","modified":1643438308409},{"_id":"source/_posts/个人随笔/自我高估自制力良好.md","hash":"a263983d8e2822fdf72e49d2cf527ce8f6a9b0af","modified":1643375702939},{"_id":"source/_posts/后端/redis作为缓存遇到问题点.md","hash":"722bc8e49c3bf0a41f0e6dd64ec6880e7aebf119","modified":1643375702939},{"_id":"source/_posts/后端/MySQL连表查询分组去重实例.md","hash":"ee56633d9435c86f6df3e50a8f0cd63f7c44c013","modified":1643375702939},{"_id":"source/_posts/个人随笔/杂七杂八瞎捣鼓.md","hash":"d1a7e5466f13ddc8fae3eaefeb2fd85645afc345","modified":1643376297521},{"_id":"source/_posts/算法/922. 按奇偶排序数组 II.md","hash":"24035547b6605689b09861ac931d5a9904527ecc","modified":1643375702939},{"_id":"source/_posts/算法/冒泡排序.md","hash":"37f9c04899e66e59c4adc83312e068ec87754d96","modified":1643375702940},{"_id":"source/_posts/算法/快速排序.md","hash":"10c67500e856a1a0a7f3b6253cc9ceba18639d53","modified":1643375702940},{"_id":"source/_posts/算法/回溯算法实战系列之全排列问题.md","hash":"6e8c07d329e1a32844213f4ca1d3c2ebddfac232","modified":1643375702940},{"_id":"source/_posts/算法/桶排序介绍.md","hash":"456baf1e55c702d28e407a32f2113681896367bb","modified":1643375702941},{"_id":"source/_posts/算法/有趣的位运算.md","hash":"0c7b0c3e8248924c50f7a91faf00236a2e9abb0a","modified":1643375702940},{"_id":"source/_posts/算法/选择排序.md","hash":"bc41d904f4ef174fc80af09be1338c07b98539cb","modified":1643375702941},{"_id":"source/medias/11.jpg","hash":"08ced9cb84cd05bad13859ab3231983cd2fdd8d4","modified":1643375702945},{"_id":"source/medias/10.jpg","hash":"b31de74f3649118f60b02c7a5993f6b318351d93","modified":1643375702944},{"_id":"source/medias/14.jpg","hash":"cd2fa3e7a2e958818fbb90d947260ea192795920","modified":1643375702948},{"_id":"source/medias/15.jpg","hash":"ac0c174181f8baf5f9acb8d04d4dd99313eba24a","modified":1643375702949},{"_id":"source/medias/3.jpg","hash":"0bd5e5dad1296c3d9551c1a869eaa7db251f52af","modified":1643375702950},{"_id":"source/medias/8.jpg","hash":"af5399f3b054d17ac0c41cccf7af80447a39e402","modified":1643375702956},{"_id":"source/medias/9.jpg","hash":"ce467516ff86f6bc9231aa10a9755329e6e82a57","modified":1643375702957},{"_id":"source/medias/archive.jpg","hash":"146e7c6cd85a1c5940c74945b1951f517884c59b","modified":1643375702959},{"_id":"source/medias/categoryDetail.jpg","hash":"0077d896369408ef41f26203e7c792ccd8d95840","modified":1643375702960},{"_id":"source/medias/friend.jpg","hash":"33f48add3cc93b05b22d4bd933c69dd1dc4164c9","modified":1643375702963},{"_id":"source/medias/comment2.jpg","hash":"0d1febd222dd098e070e6ccd732b56f93e2d3963","modified":1643375702962},{"_id":"source/medias/zfb.jpg","hash":"a3cfe867fa93906fe54556bc10f85ded59650ec8","modified":1643375703123},{"_id":"source/medias/12.jpg","hash":"18b493d884b0e472abe6a1e404b920d74d899f84","modified":1643375702946},{"_id":"source/medias/categories.jpg","hash":"6fd5bd2172bbe414d4853399d7f8538e41b9573f","modified":1643375702960},{"_id":"source/medias/comment-bg.gif","hash":"ca30cad50a1e3c723f12c24db62aa9d9fbac4da4","modified":1643375702961},{"_id":"source/medias/tagDetail.jpg","hash":"f6b3a4f16ac95ebdcfcc6ac107419c22ad12706f","modified":1643375703119},{"_id":"source/medias/wx.jpg","hash":"e1b18f99df664ccbea731a5b378ca25254efa3d2","modified":1643375703121},{"_id":"source/medias/about.jpg","hash":"24c7657d2a6830d5238daf2b917f71a9545e95ef","modified":1643375702958},{"_id":"source/medias/tag.jpg","hash":"1d9ca36570c4c9545c06eac243c9513214a56d72","modified":1643375703117},{"_id":"source/medias/13.jpg","hash":"471d551460c70d3db1e159957038317a0a7cc4f0","modified":1643375702947},{"_id":"source/medias/7.jpg","hash":"85e2e1e297f0f9de042b233f806593f53ce8c968","modified":1643375702956},{"_id":"source/medias/1.jpg","hash":"f383ab3dbad4228a045ed650ae73d383b4a9b6c6","modified":1643375702944},{"_id":"source/medias/4.jpg","hash":"7da9b1983da818f0dc78905262ed91ff045f06f6","modified":1643375702952},{"_id":"source/medias/6.jpg","hash":"d1edec3d8977a9e024a5be0396322f96e3b55cf0","modified":1643375702955},{"_id":"node_modules/hexo-theme-bamboo/README.md","hash":"c8de517c4e17b191654a6eb21618dc8b9ce5074e","modified":1643433529594},{"_id":"node_modules/hexo-theme-bamboo/package.json","hash":"916b571f9b1587ea49cd80f0045925e516c3c885","modified":1643433529593},{"_id":"node_modules/hexo-theme-bamboo/languages/default.yml","hash":"4c604dc1344630ae5ab50edc282a3e46982884c1","modified":1643433529624},{"_id":"node_modules/hexo-theme-bamboo/_config.yml","hash":"b4f06912d6e3da6fa6a59506977cc244ef48b6e1","modified":1643439747927},{"_id":"node_modules/hexo-theme-bamboo/languages/zh-CN.yml","hash":"2bf66fefa219ee8152d35bb5f823ca5096fedcf2","modified":1643433529625},{"_id":"node_modules/hexo-theme-bamboo/languages/zh-TW.yml","hash":"bd3ef201b7dcbeeee54107301550d60e71d72ba7","modified":1643433529626},{"_id":"node_modules/hexo-theme-bamboo/source/favicon.ico","hash":"801ff7b3f358b77a813787a97ef59148eec93fd8","modified":1643433529533},{"_id":"node_modules/hexo-theme-bamboo/layout/archive.ejs","hash":"2703b07cc8ac64ae46d1d263f4653013c7e1666b","modified":1643433529497},{"_id":"node_modules/hexo-theme-bamboo/layout/category.ejs","hash":"d0d19ac565414123c24b312f7158dbe1c9e275f8","modified":1643433529501},{"_id":"node_modules/hexo-theme-bamboo/layout/friends.ejs","hash":"906db16fd36cb54dd3100c08c0f206a84ddf096d","modified":1643433529505},{"_id":"node_modules/hexo-theme-bamboo/layout/index.ejs","hash":"fea918c473fe66846b7a7f94da4617610cff3d07","modified":1643433529507},{"_id":"node_modules/hexo-theme-bamboo/layout/layout.ejs","hash":"87250bb0d5181cef78d8413ac585f4f5d2b230c3","modified":1643433529511},{"_id":"node_modules/hexo-theme-bamboo/layout/tag.ejs","hash":"1061f8a9b51d983590a3efc536142a9b10acebf5","modified":1643433529529},{"_id":"node_modules/hexo-theme-bamboo/layout/tags.ejs","hash":"0c6a171fa56cf8bfa180db32f10f75c6760fd983","modified":1643433529529},{"_id":"node_modules/hexo-theme-bamboo/scripts/events/index.js","hash":"62eac296926c447c433940ec078891ec093d9f19","modified":1643433529564},{"_id":"node_modules/hexo-theme-bamboo/scripts/helpers/side_archives.js","hash":"a292f0a9e9242556b83219f519e3e92a4d85e904","modified":1643433529576},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/btn.js","hash":"0e628fa28e03f60e28f257af895b2e72a0cb8449","modified":1643433529558},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/btns.js","hash":"cb2c3b0cd78d594f3d16455c5dc6e5691c641dfc","modified":1643433529558},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/checkbox.js","hash":"49da9041bd41c57a547d42fb7a6741757b848f1c","modified":1643433529558},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/file.js","hash":"260333b277073ba8f41472cdddb35ee3e8212267","modified":1643433529562},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/folding.js","hash":"832c55a45cfeeabcd2d317d42faaee09ee54d2a4","modified":1643433529562},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/gallery.js","hash":"694a6a81dd3b3aa4a37e39b35402e99322941ec1","modified":1643433529562},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/ghcard.js","hash":"4e893d79abc1e8e1e5b3bfe08249ff32b250314d","modified":1643433529563},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/image.js","hash":"faa1d83114bc255cffc18bd0ab037f08b430f515","modified":1643433529564},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/inline-labels.js","hash":"eaaedc3d65384e0beb4306534ef4ed202b46da18","modified":1643433529568},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/issues.js","hash":"7dcb40af462e4131f6a52d354ed3b147b4e874af","modified":1643433529568},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/link.js","hash":"6ae6eca60cf4736617223c0fc5b1066d45f8ff13","modified":1643433529572},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/media.js","hash":"1d163ee349818baeb95504f82d3497da6f6556e2","modified":1643433529573},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/mermaid.js","hash":"1e69a5e4a4a5f88fdb76d0fe55ea651c14301816","modified":1643433529573},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/note.js","hash":"9e990caa1fd815a760e31f1eaa02015d357fcef8","modified":1643433529573},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/progress.js","hash":"99a10305e3924aaab05135ef25afd10d04574bfe","modified":1643433529574},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/site.js","hash":"1cb487b1435925a55eaf957d761bc08254092c36","modified":1643433529576},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/span.js","hash":"d617b5a0056c4a0c983225513c89eed6f5b56833","modified":1643433529577},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/tabs.js","hash":"133310460bdf70a7932b44c3ccca509b3f221e1c","modified":1643433529581},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/title.js","hash":"880f02544b419aed667e6eb61e8aed26259bbbda","modified":1643433529585},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/timeline.js","hash":"da2b0d7760dea698429f370aba5cded5bb24501e","modified":1643433529584},{"_id":"node_modules/hexo-theme-bamboo/scripts/tag/titleB.js","hash":"7105ca534014b33e7e81bff6e1673f9b90583e9f","modified":1643433529585},{"_id":"node_modules/hexo-theme-bamboo/scripts/z-lazyload/index.js","hash":"58b935fb699a98f0a9ceb741d2105a977e24cf59","modified":1643433529565},{"_id":"node_modules/hexo-theme-bamboo/source/css/animate.min.css","hash":"dc47ce9b8438909921b14e766febdabf3018e3c2","modified":1643433529479},{"_id":"node_modules/hexo-theme-bamboo/source/css/style.styl","hash":"b3100678b8aaabddc4dc2ce899851e164e11ec07","modified":1643433529616},{"_id":"node_modules/hexo-theme-bamboo/source/js/activate-power-mode.js","hash":"2e14b0f48c55eaec543d96ec0eb2f16e80c20c01","modified":1643433529556},{"_id":"node_modules/hexo-theme-bamboo/source/js/app.js","hash":"57f824da5f893a0c83c80522114797f09868ccf1","modified":1643433529556},{"_id":"node_modules/hexo-theme-bamboo/source/js/goTop.js","hash":"2fc5be4f18b0963fca600a77cb12348fec3aa10c","modified":1643433529563},{"_id":"node_modules/hexo-theme-bamboo/source/js/local_search.js","hash":"131d74198aa41bdb74dc27ef3ed856bc3d752f8d","modified":1643433529572},{"_id":"node_modules/hexo-theme-bamboo/source/js/ribbon.min.js","hash":"e6136a6243e04faca95844f47c21b070ade3661a","modified":1643433529574},{"_id":"node_modules/hexo-theme-bamboo/source/js/wrapImage.js","hash":"fd9072a35d48f120ac4c35e51882b83dc97b3101","modified":1643433529593},{"_id":"node_modules/hexo-theme-bamboo/source/medias/1.jpg","hash":"8be56e3deb39033e1e3e1bfcdd2053931b0d7bb5","modified":1643433529534},{"_id":"node_modules/hexo-theme-bamboo/layout/about.ejs","hash":"8127becb12c60a857f1e448cb02e1b8996c65537","modified":1643433529495},{"_id":"node_modules/hexo-theme-bamboo/layout/categories.ejs","hash":"b0f71816ca4c0899eb82b6fa100abf91b56508ab","modified":1643433529500},{"_id":"node_modules/hexo-theme-bamboo/layout/post.ejs","hash":"929a79217d5f5f8b1f000a28d55872695287d981","modified":1643433529515},{"_id":"node_modules/hexo-theme-bamboo/source/medias/2.jpg","hash":"bc25752d286c7638b2c82eae897c3bbfd1281f51","modified":1643433529540},{"_id":"node_modules/hexo-theme-bamboo/source/medias/4.jpg","hash":"b48ad74a85834f7cc354de6f0e29885d8406a0bf","modified":1643433529541},{"_id":"node_modules/hexo-theme-bamboo/source/medias/5.jpg","hash":"b40c58fa6ceaa48ea139b0ef96ba1d7a9ab2b618","modified":1643433529541},{"_id":"node_modules/hexo-theme-bamboo/source/medias/logo.png","hash":"d08165f945567a08bd74d36b1241a0b8f1618536","modified":1643433529595},{"_id":"node_modules/hexo-theme-bamboo/source/medias/wx.jpg","hash":"a76e4133f3747c83b508e4ef2cba708e3510d08a","modified":1643433529554},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/archive.ejs","hash":"246967d57c31bd873f98603536df79c1f67c96e2","modified":1643433529497},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/dark.ejs","hash":"cb74dcf56c40986eb8ab97bb6becf1b1202c3cd3","modified":1643433529503},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/goTop.ejs","hash":"d7841037d77470a314d0c4265e6380a120262c3f","modified":1643433529505},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/home_widget.ejs","hash":"0882e6992cfc2fbf1e0b05acbc1463de68f77aa4","modified":1643433529506},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/lantern.ejs","hash":"225044aa82bf305e27a00adf1a8368146e860394","modified":1643433529508},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/loaded.ejs","hash":"8f4317ac5a735a2bccb9ae07619b8f88443a555f","modified":1643433529512},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/motto.ejs","hash":"535af08125435651591be103f8e6d98c7222907d","modified":1643433529513},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/paginator.ejs","hash":"26655627ce5b1eb7050b5e24cc262cf3fc46c400","modified":1643433529514},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/side.ejs","hash":"fc498b4cf5eeaeeec81671e1bf6354de9f11e1db","modified":1643433529528},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/swiper.ejs","hash":"21ed13868e48c80650060bcaebaebb6efebfb8b5","modified":1643433529529},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/topArticle.ejs","hash":"9b321c75dbcbc424b2392e90426127182539a86d","modified":1643433529530},{"_id":"node_modules/hexo-theme-bamboo/scripts/z-lazyload/lib/process.js","hash":"48a29bdb7026c4a9c8a58190d044140a8a05a64c","modified":1643433529574},{"_id":"node_modules/hexo-theme-bamboo/source/css/_plugins/mathjax.styl","hash":"499f59db53e9c57d99bebe4722156aeca7adb8b7","modified":1643433529607},{"_id":"node_modules/hexo-theme-bamboo/source/css/_defines/variable.styl","hash":"5a92423d626110fba9cdef69676a9c028aab7dbf","modified":1643433529619},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/btn.styl","hash":"8ba55e7da020521b40498d81c9459636480608cb","modified":1643433529596},{"_id":"node_modules/hexo-theme-bamboo/source/css/_plugins/pjaxanimate.styl","hash":"f8c2d14c041bb87bc7f37d82ac939320e3d110bf","modified":1643433529609},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/checkbox.styl","hash":"dbc18a5685879493b06016c85993d4522fe48564","modified":1643433529597},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/circle.styl","hash":"c2adc73eab52952140420c2b5fc8bf134432b695","modified":1643433529598},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/folding.styl","hash":"7a88c350d302c6a89ab008b6ce2a98ed6f19c007","modified":1643433529600},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/gallery.styl","hash":"d97e1caee6862df812a172679d76db2c7ac8de62","modified":1643433529602},{"_id":"node_modules/hexo-theme-bamboo/source/medias/comment.jpg","hash":"d0e27cf8623d6bf743b5d099dfc2916bcab4e4d7","modified":1643433529547},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/image.styl","hash":"ce0c9f758f0f0be385c38d65e9bf4fb708cbaf5c","modified":1643433529606},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/link.styl","hash":"7181435bed445840bb61d655451494f83ac4d7e9","modified":1643433529607},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/note.styl","hash":"371f7c1c84921f8fe907fe994b86b04ee44f4445","modified":1643433529608},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/inline-label.styl","hash":"1903a258c5829c8370c4eb53fcb60df7f7921f08","modified":1643433529606},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/media.styl","hash":"6727008f95ad9b3146c609a2e890af009472f9e4","modified":1643433529607},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/site-card.styl","hash":"ee95cbf6072dbe3ae11e6f73a3b38a9c09e31994","modified":1643433529616},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/span.styl","hash":"bede49e1edf1049d4ea2f3dd0a17787fe084b2d2","modified":1643433529616},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/progress.styl","hash":"de1e1b08d23f95493ffda2a5375888e9e678891b","modified":1643433529612},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/tabs.styl","hash":"f26869c8e6e0815a6629bcc728614c3c8535cc92","modified":1643433529617},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/timeline.styl","hash":"ae8e4487a32606127d26dc27c74df592b2175f82","modified":1643433529618},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/title.styl","hash":"073e88057de129da751bbda06777b8c58896a993","modified":1643433529618},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/notice.ejs","hash":"ed4cad963e1a9b747864bd3ceb76bf9e763c1150","modified":1643433529513},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/base.styl","hash":"c2ea8f6c60608a1b37caa6b6d85116dadd128e26","modified":1643433529596},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/categories.styl","hash":"4d0f515056d16906273af1b498031f5ca48000a2","modified":1643433529597},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/archive.styl","hash":"bfa7625bb3b755585cab780856e805ea82bb4195","modified":1643433529596},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/category.styl","hash":"9394f99f390669ef85580e53e994e38d9a583963","modified":1643433529597},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/comment.styl","hash":"3004346401bad8e4208388b34d1dd2820dfbd2b5","modified":1643433529598},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/galleryGroup.styl","hash":"f2c7cab95d829beb7f0b7595692c428ac5613e1c","modified":1643433529603},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/custom.styl","hash":"4d97498f501d876f92006630ec7b768995c18c1d","modified":1643433529599},{"_id":"node_modules/hexo-theme-bamboo/source/css/_tag/ghcard.styl","hash":"5ac5ebba7b7725753efa06659f06cfb7bb4b2bcf","modified":1643433529603},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/copyRyght.styl","hash":"ecf67a49bb00973c84e59042427b5888f055a4ab","modified":1643433529598},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/donate.styl","hash":"a880996ca61f96ba1280d581a132deb924c4ff62","modified":1643433529600},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/drawer.styl","hash":"0498b0cf2819b681eeeec35193e491d1d039302d","modified":1643433529600},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/footer.styl","hash":"716f62778f07a9a1bada7652f2d7bd2bbb1346a9","modified":1643433529601},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/friends.styl","hash":"5a5b3a1b8689df7b948c22a8b41ba10a528d412c","modified":1643433529601},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/goTop.styl","hash":"8f47485a377750c4377611b12fc8b6932c0928c8","modified":1643433529603},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/header.styl","hash":"f59fce4bb3697cce7bcdecb8e8b37d9ed4830b12","modified":1643433529605},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/highlight.styl","hash":"44c0d8905b78cc16ca1113963fa6f54df025ca45","modified":1643433529605},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/home.styl","hash":"7f383de3c1863938f44d53761a24903faf7e3781","modified":1643433529605},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/lantern.styl","hash":"04acde311d7b9f7a732340626dbe677814ab502f","modified":1643433529606},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/motto.styl","hash":"cbaf31efcc56f481c61a4572fc3ea027fb75d1dc","modified":1643433529608},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/notice.styl","hash":"7b6890bd1c9b9339e2eb01c1470926d1463031e9","modified":1643433529608},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/pace.styl","hash":"f3073154a4e4a5a2143ed82b2a8adff2cc5b32fe","modified":1643433529609},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/paginator.styl","hash":"cdda16f2faa925bef253a98040f927044377cf22","modified":1643433529609},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/post-detail-header.styl","hash":"54b8ee3332a3b5992e73c282bea2edc89255b95e","modified":1643433529610},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/post-nav.styl","hash":"52e44096ae6d620a3a8f85d6abbde4a6bbe7da9d","modified":1643433529610},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/post.styl","hash":"026460328deeaafaa33b57d7596a18aa0eecdf16","modified":1643433529611},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/posts.styl","hash":"5e333e74b8a0064da622df618ceb0327e1581e6f","modified":1643433529611},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/side.styl","hash":"6ec3dbe47c951dff28aa95667cfab47584171d5a","modified":1643433529615},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/search.styl","hash":"33249ac553501de144a75b069d4a0c832ff24c37","modified":1643433529612},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/tag.styl","hash":"7d78f9b2d047c383cf6cf2f687eb01c812305383","modified":1643433529617},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/tags.styl","hash":"85f4a3af871dd4f008b57a57bc6751cc628a0550","modified":1643433529617},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/about.styl","hash":"96dd179c1f3e4f90f1ffa4fdc7d2b2890b88e0db","modified":1643433529595},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/topArticle.styl","hash":"6af9b8b3112ea9a033cccb0ffaab084c1481b79a","modified":1643433529618},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/danmu.styl","hash":"8aaa764bb2b1c6a49c2f6c9ee868da24a0359669","modified":1643433529599},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/transition.styl","hash":"809b40b7214cda6691b2f22ae827cbdbfaf8c303","modified":1643433529618},{"_id":"node_modules/hexo-theme-bamboo/source/js/bubble/bubble.js","hash":"57f116efe2418a389913a46909e018fa4c9b9e84","modified":1643433529558},{"_id":"node_modules/hexo-theme-bamboo/source/js/clipboard/clipboard.min.js","hash":"76fd19c15b1d0a2d7afc7b66ca5f80c9061aabe2","modified":1643433529559},{"_id":"node_modules/hexo-theme-bamboo/source/js/aplayer/APlayer@1.10.1.min.css","hash":"7f4f8913f2d46ade2def5134e2cc8684a4b87939","modified":1643433529480},{"_id":"node_modules/hexo-theme-bamboo/source/js/cursor/explosion.min.js","hash":"ed2d0a5ad306a2745b7c8180b69e36b78d4b0698","modified":1643433529561},{"_id":"node_modules/hexo-theme-bamboo/source/js/cursor/fireworks.js","hash":"86ad9484e40268952b5e32c240fb04d0268f86dd","modified":1643433529562},{"_id":"node_modules/hexo-theme-bamboo/source/js/cursor/clicklove.js","hash":"9e8e79d69ad8338761272f86fe5cad0ad5e503cc","modified":1643433529559},{"_id":"node_modules/hexo-theme-bamboo/source/js/cursor/text.js","hash":"7dd898cb00b46ceda065c92f2ac092c4ef41b4e4","modified":1643433529584},{"_id":"node_modules/hexo-theme-bamboo/source/css/_partial/dark.styl","hash":"b1b6c7cb20c09dcf9c32f82f260452e8d9bbcd2d","modified":1643433529599},{"_id":"node_modules/hexo-theme-bamboo/source/js/bubble/homeBubble.js","hash":"8475e7ed2004b9791b3f7ad4162b7a2b89467874","modified":1643433529563},{"_id":"node_modules/hexo-theme-bamboo/source/js/danmu/barrager.css","hash":"9de985f20d314f3f1182f30d1b0666e5eb9ca9b5","modified":1643433529482},{"_id":"node_modules/hexo-theme-bamboo/source/js/falling/snow.js","hash":"99222d79ff36b05200b3ff7f54f8209d8f0a364b","modified":1643433529576},{"_id":"node_modules/hexo-theme-bamboo/source/js/falling/sakura.js","hash":"b1566483a7d0deda2dd35db3d5a46f13aa5f1a86","modified":1643433529575},{"_id":"node_modules/hexo-theme-bamboo/source/js/danmu/jquery.barrager.js","hash":"72ec0d8bbd0811973152fcbb316b0dd839ffb8f3","modified":1643433529568},{"_id":"node_modules/hexo-theme-bamboo/source/js/danmu/close.png","hash":"2c3ed4345f91dc1b74a57b6dcd1e1efa9e279dbb","modified":1643433529594},{"_id":"node_modules/hexo-theme-bamboo/source/js/issues/index.js","hash":"f02538ab609541489396a682879ce854519487ca","modified":1643433529565},{"_id":"node_modules/hexo-theme-bamboo/source/js/fancybox/jquery.fancybox.min.css","hash":"1be9b79be02a1cfc5d96c4a5e0feb8f472babd95","modified":1643433529486},{"_id":"node_modules/hexo-theme-bamboo/source/js/loaded/index.css","hash":"67970197fec47832162ea29c3cf795d315cea891","modified":1643433529484},{"_id":"node_modules/hexo-theme-bamboo/source/js/pjax@0.2.8/index.js","hash":"efb9166635c18f09f2c7604a8b15d6ac8aae4870","modified":1643433529566},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism-coy.min.css","hash":"fe1246de39c25eaa7ad1b0c997ee530dbdd39ad8","modified":1643433529487},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism-funky.min.css","hash":"0220f68ccda78c2b5d1109e58f3879674c93b587","modified":1643433529488},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism-line-numbers.css","hash":"c42732535ac61ac59a4356af3d89186a3071edf1","modified":1643433529488},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism-okaidia.min.css","hash":"50be6cc15d883ff3fa5d0885fed47241695a986c","modified":1643433529488},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism-solarizedlight.min.css","hash":"927b757cd8030d12953b5c0fa6eed5de15dda8ad","modified":1643433529489},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism-tomorrow.min.css","hash":"7b4247bc4d3b719afe5957779d0e5c8fb716c8ea","modified":1643433529489},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism-twilight.min.css","hash":"ff4a6e3c4f1cb9bb59ec061656eacb750d238c15","modified":1643433529489},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism.min.css","hash":"aa405e2bcb571595c822a80f5482454c1536fa52","modified":1643433529490},{"_id":"node_modules/hexo-theme-bamboo/source/js/shareJs/share.min.css","hash":"9bd0cd6c81b60e10085cdda6aa724f147ee76599","modified":1643433529490},{"_id":"node_modules/hexo-theme-bamboo/source/js/swiper/swiper.animate1.0.3.min.js","hash":"6a8d6aa926e552a563356c36d52d1e0e0c83521e","modified":1643433529577},{"_id":"node_modules/hexo-theme-bamboo/source/js/shareJs/social-share.min.js","hash":"efdfa6b695ac6f0dd04cd8153d3e3a1a1edd90c2","modified":1643433529577},{"_id":"node_modules/hexo-theme-bamboo/source/js/swiper/swiper@5.4.1.min.css","hash":"fd618d2bdf929821d9fa70ae377b840ffc47d756","modified":1643433529491},{"_id":"node_modules/hexo-theme-bamboo/source/js/prism/prism-dark.min.css","hash":"a3f604a19e9a46f83a2fde49dfb45782748957ca","modified":1643433529488},{"_id":"node_modules/hexo-theme-bamboo/source/js/shareJs/font.css","hash":"f6407017418989fb0ced993509543fb07c6b0b33","modified":1643433529483},{"_id":"node_modules/hexo-theme-bamboo/source/js/tocbot/tocbot.css","hash":"45e469dffa7b9ebc03f99fd09fb97274cdc5e9b4","modified":1643433529492},{"_id":"node_modules/hexo-theme-bamboo/source/js/swiper/vue-awesome-swiper.js","hash":"e6f36537ed091a6b69945b1acf49e426426f1cf0","modified":1643433529590},{"_id":"node_modules/hexo-theme-bamboo/source/js/tocbot/tocbot.min.js","hash":"bc45d3586a21f7e364cd6efe58844932c00cf11c","modified":1643433529586},{"_id":"node_modules/hexo-theme-bamboo/source/js/twikoo/twikoo.all.min.js.LICENSE.txt","hash":"6e1c8f7b23f06ca4c727c805fda053dc1d9193d0","modified":1643433529622},{"_id":"node_modules/hexo-theme-bamboo/source/js/utils/index.js","hash":"fcea598ed253006d79f78d34cc36fdc6649639f3","modified":1643433529566},{"_id":"node_modules/hexo-theme-bamboo/source/js/vue-typed-js/index.css","hash":"b9dac4cfc5f0dc8854393d670b525fb63092fd38","modified":1643433529485},{"_id":"node_modules/hexo-theme-bamboo/source/js/vue-seamless-scroll/index.js","hash":"f2aaf3f9b1ab7362f7cc158e5360cb1d62a57172","modified":1643433529567},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/analytics/baidu-analytics.ejs","hash":"9e1a9d6a678e4e86951630a17f95085942e0b7e3","modified":1643433529498},{"_id":"node_modules/hexo-theme-bamboo/source/medias/cursor/Horizontal.cur","hash":"c3c5e8485a67b7ab16079a96b53aff7ff52de756","modified":1643433529495},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/analytics/baidu-push.ejs","hash":"2841870e0c625787de348221e5ddb7bbe99ec5a2","modified":1643433529499},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/analytics/google-analytics.ejs","hash":"cb7d5c76508fe8db43dbd4af9a691398fffccadb","modified":1643433529505},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/card/post.ejs","hash":"37fd6f4443620ff3b2963c19fc42bd21891428b0","modified":1643433529515},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/footer/busuanzi.ejs","hash":"bc3d2f6abc95b329dfe0186fa0364c48aab3772e","modified":1643433529500},{"_id":"node_modules/hexo-theme-bamboo/source/js/vue-typed-js/index.js","hash":"c8e6f4510eb5fe55015401510ce03f5307556b1a","modified":1643433529567},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/footer/footer.ejs","hash":"4ad6ae6bf58edbbac2651642ec7414bfd605e318","modified":1643433529505},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/head/drawer.ejs","hash":"1f78c957b472a14c13301ea6a7ec59d5ecc777e6","modified":1643433529504},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/head/head.ejs","hash":"a8b3073f4ffefb140ca6321bb8453a6b190a4a90","modified":1643433529506},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/head/search.ejs","hash":"7cbf73c577874de0b6cc89180680b1e19c5e8348","modified":1643433529521},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/head/header.ejs","hash":"e6d87db732bccbe03f0502fb8decfd81b5f309e1","modified":1643433529506},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/meta/aplayer.ejs","hash":"8175c8dc578a1f57d365e5997ea3cfd619289e37","modified":1643433529497},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/math/mathjax.ejs","hash":"84a37ec604d16df3b9828e6938128213da6f5fb0","modified":1643433529513},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/math/mermaid.ejs","hash":"2c6894abc259167170e274728467c7c7aa1ef8e5","modified":1643433529513},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/pjax/animate.ejs","hash":"93e1c0a86aba5d5b5d5c64542926bc46a49717de","modified":1643433529496},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/pjax/index.ejs","hash":"6ac774c816f9dcb7099612e2ef13bb0e7893476c","modified":1643433529506},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/post/bgSwiper.ejs","hash":"77ade59920c57fda25c2be421b77adf7b0c943d9","modified":1643433529499},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/post/categories.ejs","hash":"15f33099ef5f653b9ceb3e27f089b36bff50cc4f","modified":1643433529500},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/post/comment.ejs","hash":"08b539b2635cb3315a3b4a7be4b647970baf766f","modified":1643433529501},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/post/copyright.ejs","hash":"fd3af5c33895f907b1e5daa56d8d7266549dd019","modified":1643433529502},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/post/donate.ejs","hash":"b54c1be4bf9a4b28a8c39d2835e8b4d9ee1e56ff","modified":1643433529504},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/post/post-nav.ejs","hash":"1e92a0ca46977f94ce27540ceb09ce05bc75accd","modified":1643433529514},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/post/post-detail-header.ejs","hash":"f8365e9f530ff8c5641a7421d08d5c84049436df","modified":1643433529514},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/post/prismjs.ejs","hash":"62eb641fb1f9381166aa6c2752b4022e1a2ea52e","modified":1643433529515},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/post/share.ejs","hash":"d6e134f460383d8e0d44a74a9177385a713cf9f8","modified":1643433529522},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/post/tags.ejs","hash":"f92692427de2caa48033f975f193f9a8e4b02613","modified":1643433529529},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/scripts/copy.ejs","hash":"fda84bf47a5e7c5692f682a45f8fdcfab90900b0","modified":1643433529501},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/post/toc.ejs","hash":"4538072fe4c46406c0883a361d4f3af2da6f9c88","modified":1643433529529},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/scripts/cursor_effect.ejs","hash":"4c2a505655fb8c8d23d70584d8ea1968d1be4dcc","modified":1643433529502},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/scripts/danmu.ejs","hash":"ca20ae64fbd2527f8b54fc8618a3a0502728420c","modified":1643433529503},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/scripts/dark.ejs","hash":"340343fda6fb9bff2b853d44d3268a7fff1f4ac9","modified":1643433529503},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/scripts/falling.ejs","hash":"a8de433fc45883415a2d92c904fe7be111f6b8f0","modified":1643433529504},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/scripts/global.ejs","hash":"e33fa55c18918cc22f211b8fe442cb68e5225bd6","modified":1643433529505},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/scripts/head.ejs","hash":"4536885880315fb90efd75935c133051a729d45c","modified":1643433529506},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/scripts/index.ejs","hash":"66fb416cdecaf9402f5083cb1ab09fc62508d255","modified":1643433529507},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/scripts/inputEffects.ejs","hash":"765c69436e021412dd8bbb852ea2403c97fc6adf","modified":1643433529507},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/scripts/lazyload.ejs","hash":"6195374711fd384887eb1c35a46c43f198ebd079","modified":1643433529512},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/scripts/issues.ejs","hash":"cf5436f10fb9a2fb7238a1c528a5ed64a2345840","modified":1643433529507},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/scripts/scrollreveal.ejs","hash":"4aba6d5b506b3a8fc7d84abe0d42875e0107d64e","modified":1643433529518},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/scripts/setHeader.ejs","hash":"a76903748b33d745ec76ae3e8e8622d2c6b9ffbb","modified":1643433529522},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/scripts/toc.ejs","hash":"d3ad4e532e38841447256c001bad39a10cc7b5ae","modified":1643433529530},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/side/sideHeader.ejs","hash":"87a5eb0f31b1c6581652162861970563a5f035c5","modified":1643433529528},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/scripts/typed.ejs","hash":"262725f946bb3ae8957b8e3d50c1a7cd564f8866","modified":1643433529530},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/side/side_archives.ejs","hash":"c82b7c669aaaa2b9575cf6daf6d0a133b64acfd0","modified":1643433529523},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/side/side_blogger.ejs","hash":"a2c637abf7943b273edfb69d0d8e0dc812c84127","modified":1643433529523},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/side/side_category.ejs","hash":"dccd4537a94cf6e210803d6ab2789e6cd57d755e","modified":1643433529525},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/side/side_recent_post.ejs","hash":"7fe61d14865e97988ff5d42047abb4a4ee8af7f0","modified":1643433529526},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/side/side_tagcloud.ejs","hash":"7e716ce939cb8dd4004896adf41559d57bcfff0e","modified":1643433529526},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/side/side_webinfo.ejs","hash":"1efe51b2685b7c4ad2ab42849c5ebe59e2d20def","modified":1643433529527},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/side/widget_library_sticky.ejs","hash":"e3929f7edf85900e7becc71e0cbe14da2333f621","modified":1643433529530},{"_id":"node_modules/hexo-theme-bamboo/source/js/shareJs/fonts/iconfont.ttf","hash":"afd898f59d363887418669520b24d175f966a083","modified":1643433529622},{"_id":"node_modules/hexo-theme-bamboo/source/js/shareJs/fonts/iconfont.svg","hash":"337b4f156f6d8f4beb32c32a3db46fef361cff74","modified":1643433529620},{"_id":"node_modules/hexo-theme-bamboo/source/js/shareJs/fonts/iconfont.eot","hash":"00ff749c8e202401190cc98d56087cdda716abe4","modified":1643433529532},{"_id":"node_modules/hexo-theme-bamboo/source/js/shareJs/fonts/iconfont.woff","hash":"2e3fce1dcfbd6e2114e7bfbeaf72d3c62e15a1bd","modified":1643433529623},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/comment/changyan/layout.ejs","hash":"46192143a90303d8924b3d07d28df116bc833894","modified":1643433529508},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/comment/changyan/script.ejs","hash":"c357b9052564e12754cf21a1cb1debd3bdfe1eac","modified":1643433529516},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/comment/gitalk/layout.ejs","hash":"8a4c57646ee0d4a4e94d568708fb85a8f9ac97e7","modified":1643433529509},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/comment/gitment/layout.ejs","hash":"353820d6d6aade09cd21b31585afa20485008083","modified":1643433529509},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/comment/gitalk/script.ejs","hash":"733947cad238d89c5a5694ecf19a83b1d5648ab9","modified":1643433529516},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/comment/gitment/script.ejs","hash":"1e02cf43a347a612796aa188446605e213e0dd51","modified":1643433529516},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/comment/livere/layout.ejs","hash":"f88b32604056721e658c25f775866a1519e714f2","modified":1643433529510},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/comment/livere/script.ejs","hash":"b33339cfa1429947cf44f9cb41a5996865467cc3","modified":1643433529517},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/comment/twikoo/script.ejs","hash":"655e305e6a9c189a49f88b086c8694e50ecfb37d","modified":1643433529517},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/comment/twikoo/layout.ejs","hash":"c51eab2274374330820b29d3a9e69b3273433f9f","modified":1643433529510},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/comment/utterance/layout.ejs","hash":"eab867c580f6184d068d5fcc545a763a2919eb16","modified":1643433529511},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/comment/utterance/script.ejs","hash":"5d4aa3f60f0f648a5347b29eceef3c7244cb7b96","modified":1643433529517},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/comment/valine/layout.ejs","hash":"ce02592c66f0309f85f13d57bfd5bac8234cec6e","modified":1643433529511},{"_id":"node_modules/hexo-theme-bamboo/layout/_partial/comment/valine/script.ejs","hash":"c39459b0fb46bb1eb49823cc62375f04d3b4a48e","modified":1643433529518},{"_id":"node_modules/hexo-theme-bamboo/source/js/jquery3.5.1.js","hash":"29fa5ad995e9ec866ece1d3d0b698fc556580eee","modified":1643433529571},{"_id":"node_modules/hexo-theme-bamboo/source/medias/10.jpg","hash":"b31de74f3649118f60b02c7a5993f6b318351d93","modified":1643433529535},{"_id":"node_modules/hexo-theme-bamboo/source/medias/11.jpg","hash":"08ced9cb84cd05bad13859ab3231983cd2fdd8d4","modified":1643433529536},{"_id":"node_modules/hexo-theme-bamboo/source/medias/13.jpg","hash":"302a8d12b56952cd67c225aaf6557af5d2a95d8c","modified":1643433529537},{"_id":"node_modules/hexo-theme-bamboo/source/medias/12.jpg","hash":"fe65ad1a71794c32196bb774c1a140754278dc58","modified":1643433529536},{"_id":"node_modules/hexo-theme-bamboo/source/medias/15.jpg","hash":"ac0c174181f8baf5f9acb8d04d4dd99313eba24a","modified":1643433529538},{"_id":"node_modules/hexo-theme-bamboo/source/medias/14.jpg","hash":"cd2fa3e7a2e958818fbb90d947260ea192795920","modified":1643433529538},{"_id":"node_modules/hexo-theme-bamboo/source/medias/3.jpg","hash":"0bd5e5dad1296c3d9551c1a869eaa7db251f52af","modified":1643433529541},{"_id":"node_modules/hexo-theme-bamboo/source/medias/8.jpg","hash":"af5399f3b054d17ac0c41cccf7af80447a39e402","modified":1643433529543},{"_id":"node_modules/hexo-theme-bamboo/source/medias/6.jpg","hash":"a9701435f9d204bfece97e192f4603d615ec8ee4","modified":1643433529542},{"_id":"node_modules/hexo-theme-bamboo/source/medias/archive.jpg","hash":"146e7c6cd85a1c5940c74945b1951f517884c59b","modified":1643433529546},{"_id":"node_modules/hexo-theme-bamboo/source/medias/9.jpg","hash":"ce467516ff86f6bc9231aa10a9755329e6e82a57","modified":1643433529544},{"_id":"node_modules/hexo-theme-bamboo/source/medias/comment2.jpg","hash":"0d1febd222dd098e070e6ccd732b56f93e2d3963","modified":1643433529548},{"_id":"node_modules/hexo-theme-bamboo/source/medias/friend.jpg","hash":"33f48add3cc93b05b22d4bd933c69dd1dc4164c9","modified":1643433529548},{"_id":"node_modules/hexo-theme-bamboo/source/medias/zfb.jpg","hash":"8a2cb7c67bdcd954e3feb9293b78895ec836d46f","modified":1643433529555},{"_id":"node_modules/hexo-theme-bamboo/source/medias/7.jpg","hash":"0db93ed9af4a13108ea4f2156b7b0fab9df3b894","modified":1643433529543},{"_id":"node_modules/hexo-theme-bamboo/source/medias/categoryDetail.jpg","hash":"0077d896369408ef41f26203e7c792ccd8d95840","modified":1643433529547},{"_id":"node_modules/hexo-theme-bamboo/source/js/fancybox/jquery.fancybox.min.js","hash":"eef46b6fb2e460838cd7328a6e13ecda0cb1e194","modified":1643433529569},{"_id":"node_modules/hexo-theme-bamboo/source/medias/categories.jpg","hash":"6fd5bd2172bbe414d4853399d7f8538e41b9573f","modified":1643433529546},{"_id":"node_modules/hexo-theme-bamboo/source/medias/comment-bg.gif","hash":"ca30cad50a1e3c723f12c24db62aa9d9fbac4da4","modified":1643433529533},{"_id":"node_modules/hexo-theme-bamboo/source/medias/tagDetail.jpg","hash":"f6b3a4f16ac95ebdcfcc6ac107419c22ad12706f","modified":1643433529551},{"_id":"node_modules/hexo-theme-bamboo/source/js/swiper/swiper.min.js","hash":"674fa0bd5973cc8124d6a711c725b119c025da0c","modified":1643433529580},{"_id":"node_modules/hexo-theme-bamboo/source/js/valine/av-min@3.0.4.js","hash":"ba7a630163b60339f87bb4ff2b7577e316e68ccd","modified":1643433529557},{"_id":"node_modules/hexo-theme-bamboo/source/medias/about.jpg","hash":"24c7657d2a6830d5238daf2b917f71a9545e95ef","modified":1643433529545},{"_id":"node_modules/hexo-theme-bamboo/source/medias/tag.jpg","hash":"1d9ca36570c4c9545c06eac243c9513214a56d72","modified":1643433529549},{"_id":"node_modules/hexo-theme-bamboo/source/js/vue2.6.11.js","hash":"1159f02f3f7191a5cf4c109734d0268173fab96d","modified":1643433529592},{"_id":"node_modules/hexo-theme-bamboo/source/js/twikoo/twikoo.all.min.js","hash":"d1ec95821873a81eddf4e5698698b39d54d2a8cc","modified":1643433529589},{"_id":"source/medias/images/QUI.gif","hash":"21e1ef7f5563b1c8fde7412b03affad131a8d86b","modified":1643375703108},{"_id":"public/atom.xml","hash":"5d1012a7c19b542a601217320e46c63d3e15ed07","modified":1643443599591},{"_id":"public/search.xml","hash":"8427e99acc57dccc019d039bebe52b8f1d1fec46","modified":1643443599591},{"_id":"public/about/index.html","hash":"7e8fd5faf3a0d8684cb6f5be381a4e55c47f46a1","modified":1643443599591},{"_id":"public/bizhi/index.html","hash":"58758eabc15a1c4ee21dfefd7863f630fb8f3e53","modified":1643443599591},{"_id":"public/categories/index.html","hash":"3fe82198111767f0dee69ff9d880f82c6813b099","modified":1643443599591},{"_id":"public/friends/index.html","hash":"259fbe7407e4fc0dc4d9f31fe715f83a75fbb2d9","modified":1643443599591},{"_id":"public/gallery/index.html","hash":"6dd55a07788ac12c29fdbac5892753fd9a9e4584","modified":1643443599591},{"_id":"public/tags/index.html","hash":"5d18ac41c6d44b52ee3873ceba6ae5973d6eb530","modified":1643443599591},{"_id":"public/2021/08/03/hou-duan/redis-zuo-wei-huan-cun-yu-dao-wen-ti-dian/index.html","hash":"d97dc076bf7856a36d008e698a5a3951ca8c3072","modified":1643443599591},{"_id":"public/2021/07/23/suan-fa/you-qu-de-wei-yun-suan/index.html","hash":"19d91766ec3e9af723074bc086ee6c6ecc0cbd7a","modified":1643443599591},{"_id":"public/2021/07/22/ge-ren-sui-bi/za-qi-za-ba-xia-dao-gu/index.html","hash":"b7892b7a792e143f958c5c9de51c102031833453","modified":1643443599591},{"_id":"public/2021/07/20/ge-ren-sui-bi/zi-wo-gao-gu-zi-zhi-li-liang-hao/index.html","hash":"a5a5d2728337d163417e5b4c1c7570a27f2eca3a","modified":1643443599591},{"_id":"public/2021/07/03/du-shu-da-ben-ying/index.html","hash":"2649b73853057e82280a7ac4414283d9ae8cb509","modified":1643443599591},{"_id":"public/2021/06/27/suan-fa/hui-su-suan-fa-shi-zhan-xi-lie-zhi-quan-pai-lie-wen-ti/index.html","hash":"9d8ed05f39cb2a7158d569e158d6de6c0e358515","modified":1643443599591},{"_id":"public/2021/06/27/hou-duan/mysql-lian-biao-cha-xun-fen-zu-qu-chong-shi-li/index.html","hash":"63ab334243639d553e493aac68df19cb9215a778","modified":1643443599591},{"_id":"public/2021/06/20/suan-fa/kuai-su-pai-xu/index.html","hash":"8059e406ed6413a0de1fad5a4fbc909b63e1ef02","modified":1643443599591},{"_id":"public/2021/06/19/suan-fa/tong-pai-xu-jie-shao/index.html","hash":"1ef26bdd39eaad67055e1f2eaa98cf1e2b6b8da6","modified":1643443599591},{"_id":"public/2021/06/19/suan-fa/922.an-qi-ou-pai-xu-shu-zu-ii/index.html","hash":"1c4fe460ccfac63534e6aea4ea8f1bf16a10d796","modified":1643443599591},{"_id":"public/2021/06/19/suan-fa/mou-pao-pai-xu/index.html","hash":"faa61dbda50b8a5e4608c50479dff4624c2fd9cf","modified":1643443599591},{"_id":"public/2021/06/19/suan-fa/xuan-ze-pai-xu/index.html","hash":"b9c11069bf569c4197167cd1a5026aee0da15705","modified":1643443599591},{"_id":"public/categories/读书大本营/index.html","hash":"353be49aba0a776154492c5bdaab8e5defa1235d","modified":1643443599591},{"_id":"public/categories/个人随笔/index.html","hash":"f91c6f65128049a07658de08a5cfcf0916ec061c","modified":1643443599591},{"_id":"public/categories/后端/index.html","hash":"78ec4b5ef7e3d87b4b82f84b17178a962e6800a2","modified":1643443599591},{"_id":"public/categories/算法/index.html","hash":"18f4f507c147d518d6fa2115575ba72af5de6fa4","modified":1643443599591},{"_id":"public/archives/index.html","hash":"d4cfda301bc8d2ccc43efeac3c1f48e084b03b06","modified":1643443599591},{"_id":"public/archives/page/2/index.html","hash":"3fafb8553c2d732409912f439cbf32a66c635af3","modified":1643443599591},{"_id":"public/archives/2021/index.html","hash":"098433123330b5ed14471a503797ea5ee0453a2e","modified":1643443599591},{"_id":"public/archives/2021/page/2/index.html","hash":"6cc673f818fc3d0510980d558fc056de268d9b8b","modified":1643443599591},{"_id":"public/archives/2021/06/index.html","hash":"aebb3d960a4d5db844a1ebad6308c9efbbfa11dd","modified":1643443599591},{"_id":"public/archives/2021/07/index.html","hash":"cc7e691d1f6f4e460e38e8ce9bf2bffff4d6a668","modified":1643443599591},{"_id":"public/archives/2021/08/index.html","hash":"c1708f0f38bd49a79711bd1950392b4e0a636859","modified":1643443599591},{"_id":"public/index.html","hash":"df7b8b1b727432a7503dc746b13e5a1e269a6e76","modified":1643443599591},{"_id":"public/tags/读书/index.html","hash":"1f5ce0006db84b778ead8f209fc0d0676783cca5","modified":1643443599591},{"_id":"public/page/2/index.html","hash":"b54a60344b3cd504fff0d83497e53b33b3951c5b","modified":1643443599591},{"_id":"public/tags/瞎捣鼓/index.html","hash":"9b604c471b8a642f0b044a65c84ce17a7082ca56","modified":1643443599591},{"_id":"public/tags/个人随笔/index.html","hash":"edcd3057d15551d14ecda2b9207c12e8729743a9","modified":1643443599591},{"_id":"public/tags/自制力/index.html","hash":"ef6c07a4741fbeb939680f2f894bb8b49e291791","modified":1643443599591},{"_id":"public/tags/MySQL/index.html","hash":"5ab594c45a2ef4e37a11721eb1318011f0c09caf","modified":1643443599591},{"_id":"public/tags/redis/index.html","hash":"d39e4c9b5a0906eeabb218ec0799cc74dd06f55d","modified":1643443599591},{"_id":"public/tags/算法/index.html","hash":"ed53e4e39deb68d95dc6240511047f3262b65367","modified":1643443599591},{"_id":"public/tags/刷题/index.html","hash":"3487033b4f6f11491419fb068fa0e7cf60860f5e","modified":1643443599591},{"_id":"public/tags/排序/index.html","hash":"d78fd07480f80816e1d99ed0c3cc12cd05cdc300","modified":1643443599591},{"_id":"public/tags/回溯算法/index.html","hash":"ae7df0891408eeee7a77f04c91043fa49cccbe07","modified":1643443599591},{"_id":"public/tags/学习/index.html","hash":"2619f4d2f81d368cfe9f082de62254d711930eaa","modified":1643443599591},{"_id":"public/favicon.ico","hash":"801ff7b3f358b77a813787a97ef59148eec93fd8","modified":1643443599591},{"_id":"public/medias/2.jpg","hash":"bc25752d286c7638b2c82eae897c3bbfd1281f51","modified":1643443599591},{"_id":"public/medias/5.jpg","hash":"b40c58fa6ceaa48ea139b0ef96ba1d7a9ab2b618","modified":1643443599591},{"_id":"public/medias/comment.jpg","hash":"d0e27cf8623d6bf743b5d099dfc2916bcab4e4d7","modified":1643443599591},{"_id":"public/medias/logo.png","hash":"7a6561cc59bceb362ce62c4a4e2c45d1144267dd","modified":1643443599591},{"_id":"public/js/twikoo/twikoo.all.min.js.LICENSE.txt","hash":"6e1c8f7b23f06ca4c727c805fda053dc1d9193d0","modified":1643443599591},{"_id":"public/js/danmu/close.png","hash":"2c3ed4345f91dc1b74a57b6dcd1e1efa9e279dbb","modified":1643443599591},{"_id":"public/js/shareJs/fonts/iconfont.svg","hash":"337b4f156f6d8f4beb32c32a3db46fef361cff74","modified":1643443599591},{"_id":"public/medias/cursor/Horizontal.cur","hash":"c3c5e8485a67b7ab16079a96b53aff7ff52de756","modified":1643443599591},{"_id":"public/js/shareJs/fonts/iconfont.ttf","hash":"afd898f59d363887418669520b24d175f966a083","modified":1643443599591},{"_id":"public/js/shareJs/fonts/iconfont.eot","hash":"00ff749c8e202401190cc98d56087cdda716abe4","modified":1643443599591},{"_id":"public/js/shareJs/fonts/iconfont.woff","hash":"2e3fce1dcfbd6e2114e7bfbeaf72d3c62e15a1bd","modified":1643443599591},{"_id":"public/062202062582_0logo.ico","hash":"a84dd50428df3cdf4da641f47255323776734bf1","modified":1643443599591},{"_id":"public/medias/11.jpg","hash":"08ced9cb84cd05bad13859ab3231983cd2fdd8d4","modified":1643443599591},{"_id":"public/medias/14.jpg","hash":"cd2fa3e7a2e958818fbb90d947260ea192795920","modified":1643443599591},{"_id":"public/medias/15.jpg","hash":"ac0c174181f8baf5f9acb8d04d4dd99313eba24a","modified":1643443599591},{"_id":"public/medias/3.jpg","hash":"0bd5e5dad1296c3d9551c1a869eaa7db251f52af","modified":1643443599591},{"_id":"public/medias/9.jpg","hash":"ce467516ff86f6bc9231aa10a9755329e6e82a57","modified":1643443599591},{"_id":"public/medias/archive.jpg","hash":"146e7c6cd85a1c5940c74945b1951f517884c59b","modified":1643443599591},{"_id":"public/medias/8.jpg","hash":"af5399f3b054d17ac0c41cccf7af80447a39e402","modified":1643443599591},{"_id":"public/medias/categoryDetail.jpg","hash":"0077d896369408ef41f26203e7c792ccd8d95840","modified":1643443599591},{"_id":"public/medias/comment2.jpg","hash":"0d1febd222dd098e070e6ccd732b56f93e2d3963","modified":1643443599591},{"_id":"public/medias/friend.jpg","hash":"33f48add3cc93b05b22d4bd933c69dd1dc4164c9","modified":1643443599591},{"_id":"public/medias/10.jpg","hash":"b31de74f3649118f60b02c7a5993f6b318351d93","modified":1643443599591},{"_id":"public/medias/zfb.jpg","hash":"a3cfe867fa93906fe54556bc10f85ded59650ec8","modified":1643443599591},{"_id":"public/js/activate-power-mode.js","hash":"3d02584da9dd820d1d9a454c5a93a2c37a8e4e42","modified":1643443599591},{"_id":"public/js/app.js","hash":"38e8d7ce69449ee7fc28db92f6be88ae26e708b2","modified":1643443599591},{"_id":"public/js/goTop.js","hash":"dfcbf8a70cfb4465d0afabf5153bd069771a6a1c","modified":1643443599591},{"_id":"public/js/ribbon.min.js","hash":"3c8e4d717ca107f3723def1795c8ed62a5f1a8d0","modified":1643443599591},{"_id":"public/js/local_search.js","hash":"475dc0727cb85c22f15f86701dd93c4bf449a438","modified":1643443599591},{"_id":"public/js/wrapImage.js","hash":"4b3cbceda7950c3fb2a17c4e169c4fdbc023ceab","modified":1643443599591},{"_id":"public/js/aplayer/APlayer@1.10.1.min.css","hash":"07372a2ba507388d0fed166d761b1c2c2a659dce","modified":1643443599591},{"_id":"public/js/bubble/bubble.js","hash":"40cbc57f98407216ba6dc412e2b75e18c036240f","modified":1643443599591},{"_id":"public/js/bubble/homeBubble.js","hash":"a8635136621c8c54c04462932192a94f314942cb","modified":1643443599591},{"_id":"public/js/clipboard/clipboard.min.js","hash":"6371ec0a8e242395c7d4d008d2b98e472c9dcc52","modified":1643443599591},{"_id":"public/js/cursor/explosion.min.js","hash":"ed2d0a5ad306a2745b7c8180b69e36b78d4b0698","modified":1643443599591},{"_id":"public/js/cursor/fireworks.js","hash":"6e1e9206549a6a1a4f5a8672a2dc5044a8f691bd","modified":1643443599591},{"_id":"public/js/cursor/clicklove.js","hash":"9e8e79d69ad8338761272f86fe5cad0ad5e503cc","modified":1643443599591},{"_id":"public/js/cursor/text.js","hash":"a015017310e601f1e544cbc4b08c35b8e547c939","modified":1643443599591},{"_id":"public/js/falling/snow.js","hash":"6f4ef88304f874ef8bb8ea54f79b5d97f5a8f2f6","modified":1643443599591},{"_id":"public/js/danmu/barrager.css","hash":"3691efec6dd3d554b4a3dd20ef04836459f151a8","modified":1643443599591},{"_id":"public/js/danmu/jquery.barrager.js","hash":"305d6e93f3de102b5e1e9b1373821c849d8f54cb","modified":1643443599591},{"_id":"public/js/fancybox/jquery.fancybox.min.css","hash":"1be9b79be02a1cfc5d96c4a5e0feb8f472babd95","modified":1643443599591},{"_id":"public/js/loaded/index.css","hash":"6ffc29024687d49fda0d474dd4a94fc706b8d7fc","modified":1643443599591},{"_id":"public/js/issues/index.js","hash":"e5f7b37f9dd8e966c7a63b8b6da27d53510eddeb","modified":1643443599591},{"_id":"public/js/prism/prism-funky.min.css","hash":"0220f68ccda78c2b5d1109e58f3879674c93b587","modified":1643443599591},{"_id":"public/js/prism/prism-coy.min.css","hash":"fe1246de39c25eaa7ad1b0c997ee530dbdd39ad8","modified":1643443599591},{"_id":"public/js/prism/prism-dark.min.css","hash":"a3f604a19e9a46f83a2fde49dfb45782748957ca","modified":1643443599591},{"_id":"public/js/prism/prism-line-numbers.css","hash":"3b64b50b73729de943ec894c1d6f19115fa81624","modified":1643443599591},{"_id":"public/js/prism/prism-okaidia.min.css","hash":"50be6cc15d883ff3fa5d0885fed47241695a986c","modified":1643443599591},{"_id":"public/js/prism/prism-solarizedlight.min.css","hash":"927b757cd8030d12953b5c0fa6eed5de15dda8ad","modified":1643443599591},{"_id":"public/js/prism/prism-tomorrow.min.css","hash":"7b4247bc4d3b719afe5957779d0e5c8fb716c8ea","modified":1643443599591},{"_id":"public/js/prism/prism-twilight.min.css","hash":"ff4a6e3c4f1cb9bb59ec061656eacb750d238c15","modified":1643443599591},{"_id":"public/js/prism/prism.min.css","hash":"aa405e2bcb571595c822a80f5482454c1536fa52","modified":1643443599591},{"_id":"public/js/shareJs/font.css","hash":"9d909397e4e94f696b7dd90a16481b50cf170362","modified":1643443599591},{"_id":"public/js/shareJs/share.min.css","hash":"573c7dddb465efd5f5a9337bd50a1ed3f8e82cff","modified":1643443599591},{"_id":"public/js/swiper/swiper.animate1.0.3.min.js","hash":"0e48f180ca2f18b787e4b7b6e55ee3b0c6067691","modified":1643443599591},{"_id":"public/js/swiper/swiper@5.4.1.min.css","hash":"de2263f82e7bf0778f31fd05c53000799f60701a","modified":1643443599591},{"_id":"public/js/tocbot/tocbot.css","hash":"45e469dffa7b9ebc03f99fd09fb97274cdc5e9b4","modified":1643443599591},{"_id":"public/js/tocbot/tocbot.min.js","hash":"bc45d3586a21f7e364cd6efe58844932c00cf11c","modified":1643443599591},{"_id":"public/js/utils/index.js","hash":"54c66b0a396cc3743884cdb979e5c400218613ce","modified":1643443599591},{"_id":"public/js/vue-seamless-scroll/index.js","hash":"f2aaf3f9b1ab7362f7cc158e5360cb1d62a57172","modified":1643443599591},{"_id":"public/js/vue-typed-js/index.css","hash":"36a1d2f61d11ab328e349d6a523dd9dea2ec7ee1","modified":1643443599591},{"_id":"public/css/style.css","hash":"e109e098dcbee11198e9b89bea1e2f7ec40bde2a","modified":1643443599591},{"_id":"public/css/animate.min.css","hash":"8411c1c0418521c96d07bcca0d9dbce7e832ccc9","modified":1643443599591},{"_id":"public/js/jquery3.5.1.js","hash":"d2cc8d43ce1c854b1172e42b1209502ad563db83","modified":1643443599591},{"_id":"public/js/falling/sakura.js","hash":"ab41921e8f6ea1bedfcc348924574dc0caa20858","modified":1643443599591},{"_id":"public/js/vue2.6.11.js","hash":"e793aa33ef33150eaba3bc02b07455a231f053ad","modified":1643443599591},{"_id":"public/js/fancybox/jquery.fancybox.min.js","hash":"6181412e73966696d08e1e5b1243a572d0f22ba6","modified":1643443599591},{"_id":"public/js/pjax@0.2.8/index.js","hash":"c9b1e349203e558dbe43665353e88c6eafc7dbcd","modified":1643443599591},{"_id":"public/js/shareJs/social-share.min.js","hash":"efdfa6b695ac6f0dd04cd8153d3e3a1a1edd90c2","modified":1643443599591},{"_id":"public/js/swiper/vue-awesome-swiper.js","hash":"b7a1ab21dfc58272009bfb5cb7ab87b79f5df573","modified":1643443599591},{"_id":"public/js/swiper/swiper.min.js","hash":"a2fe3c0df9196597c283b2f6ffecc1d4d8702245","modified":1643443599591},{"_id":"public/js/vue-typed-js/index.js","hash":"0d80f25135de943ccdfdebec23275bd82712fae1","modified":1643443599591},{"_id":"public/js/valine/av-min@3.0.4.js","hash":"6d7100ab357ac92291901dbbf0d4c683d05a7672","modified":1643443599591},{"_id":"public/js/twikoo/twikoo.all.min.js","hash":"c3f5f0a69b7864e7ef5bbf99fc774bec37947d7c","modified":1643443599591},{"_id":"public/medias/12.jpg","hash":"18b493d884b0e472abe6a1e404b920d74d899f84","modified":1643443599591},{"_id":"public/medias/categories.jpg","hash":"6fd5bd2172bbe414d4853399d7f8538e41b9573f","modified":1643443599591},{"_id":"public/medias/comment-bg.gif","hash":"ca30cad50a1e3c723f12c24db62aa9d9fbac4da4","modified":1643443599591},{"_id":"public/medias/tagDetail.jpg","hash":"f6b3a4f16ac95ebdcfcc6ac107419c22ad12706f","modified":1643443599591},{"_id":"public/medias/wx.jpg","hash":"e1b18f99df664ccbea731a5b378ca25254efa3d2","modified":1643443599591},{"_id":"public/medias/about.jpg","hash":"24c7657d2a6830d5238daf2b917f71a9545e95ef","modified":1643443599591},{"_id":"public/medias/tag.jpg","hash":"1d9ca36570c4c9545c06eac243c9513214a56d72","modified":1643443599591},{"_id":"public/medias/13.jpg","hash":"471d551460c70d3db1e159957038317a0a7cc4f0","modified":1643443599591},{"_id":"public/medias/7.jpg","hash":"85e2e1e297f0f9de042b233f806593f53ce8c968","modified":1643443599591},{"_id":"public/medias/4.jpg","hash":"7da9b1983da818f0dc78905262ed91ff045f06f6","modified":1643443599591},{"_id":"public/medias/6.jpg","hash":"d1edec3d8977a9e024a5be0396322f96e3b55cf0","modified":1643443599591},{"_id":"public/medias/1.jpg","hash":"f383ab3dbad4228a045ed650ae73d383b4a9b6c6","modified":1643443599591},{"_id":"public/medias/images/QUI.gif","hash":"21e1ef7f5563b1c8fde7412b03affad131a8d86b","modified":1643443599591}],"Category":[{"name":"读书大本营","_id":"ckyzjvxnl0004sdwo7hs48pwd"},{"name":"个人随笔","_id":"ckyzjvxnq000csdwo4hd5bmjf"},{"name":"后端","_id":"ckyzjvxny000osdwofho1brak"},{"name":"算法","_id":"ckyzjvxo2000xsdwo1dua3s59"}],"Data":[],"Page":[{"title":"关于","date":"2022-01-29T05:56:37.000Z","type":"about","layout":"about","_content":"","source":"about/index.md","raw":"---\ntitle: 关于\ndate: 2022-01-29 13:56:37\ntype: \"about\"\nlayout: \"about\"\n---\n","updated":"2022-01-29T06:37:43.820Z","path":"about/index.html","comments":1,"_id":"ckyzjvxne0000sdwo1hao3ugi","content":"","site":{"data":{}},"excerpt":"","more":""},{"title":"壁纸","date":"2021-05-10T07:39:04.000Z","toc":false,"img":"https://pic1.zhimg.com/80/v2-92cc20bdf4674b6c6337478bb06657b3_1440w.jpg?source=1940ef5c","onlyTitle":true,"_content":"{% gallery %}\n![图片描述](https://pic4.zhimg.com/80/v2-5dfab6525ec92b4caf3f09e1ee72a23b_1440w.jpg?source=1940ef5c)\n![图片描述](https://pic4.zhimg.com/80/v2-5c062983ace7db9601880019190fb5a8_1440w.jpg?source=1940ef5c)\n{% endgallery %}\n{% gallery %}\n![图片描述](https://pic1.zhimg.com/80/v2-154228684029ae0c2183f65a9568c310_1440w.jpg?source=1940ef5c)\n![图片描述](https://pic4.zhimg.com/80/v2-121618e14ad58dcedf8637127087ff27_1440w.jpg?source=1940ef5c)\n![图片描述](https://pic2.zhimg.com/80/v2-d61b1af36a619fec1b32775d75f4900d_1440w.jpg?source=1940ef5c)\n![图片描述](https://pic3.zhimg.com/80/v2-f94047ce45907e0966a681089835c04d_1440w.jpg?source=1940ef5c)\n{% endgallery %}\n{% gallery %}\n![图片描述](https://pic4.zhimg.com/80/v2-604a15cef201cf177943af2d915eb2e7_1440w.jpg?source=1940ef5c)\n![图片描述](https://pic1.zhimg.com/80/v2-bf6c555e7c61a57ba4a1fd95a9a32975_1440w.jpg?source=1940ef5c)\n{% endgallery %}\n\n","source":"bizhi/index.md","raw":"---\ntitle: 壁纸\ndate: 2021-05-10 15:39:04\ntoc: false\nimg: https://pic1.zhimg.com/80/v2-92cc20bdf4674b6c6337478bb06657b3_1440w.jpg?source=1940ef5c\nonlyTitle: true\n---\n{% gallery %}\n![图片描述](https://pic4.zhimg.com/80/v2-5dfab6525ec92b4caf3f09e1ee72a23b_1440w.jpg?source=1940ef5c)\n![图片描述](https://pic4.zhimg.com/80/v2-5c062983ace7db9601880019190fb5a8_1440w.jpg?source=1940ef5c)\n{% endgallery %}\n{% gallery %}\n![图片描述](https://pic1.zhimg.com/80/v2-154228684029ae0c2183f65a9568c310_1440w.jpg?source=1940ef5c)\n![图片描述](https://pic4.zhimg.com/80/v2-121618e14ad58dcedf8637127087ff27_1440w.jpg?source=1940ef5c)\n![图片描述](https://pic2.zhimg.com/80/v2-d61b1af36a619fec1b32775d75f4900d_1440w.jpg?source=1940ef5c)\n![图片描述](https://pic3.zhimg.com/80/v2-f94047ce45907e0966a681089835c04d_1440w.jpg?source=1940ef5c)\n{% endgallery %}\n{% gallery %}\n![图片描述](https://pic4.zhimg.com/80/v2-604a15cef201cf177943af2d915eb2e7_1440w.jpg?source=1940ef5c)\n![图片描述](https://pic1.zhimg.com/80/v2-bf6c555e7c61a57ba4a1fd95a9a32975_1440w.jpg?source=1940ef5c)\n{% endgallery %}\n\n","updated":"2022-01-29T06:43:09.029Z","path":"bizhi/index.html","comments":1,"layout":"page","_id":"ckyzjvxnk0002sdwo8a1709fx","content":"<div class=\"gallery \">\n              <p><img src=\"https://pic4.zhimg.com/80/v2-5dfab6525ec92b4caf3f09e1ee72a23b_1440w.jpg?source=1940ef5c\" class=\"lazyload placeholder\" data-srcset=\"https://pic4.zhimg.com/80/v2-5dfab6525ec92b4caf3f09e1ee72a23b_1440w.jpg?source=1940ef5c\" srcset=\"https://img2.baidu.com/it/u=2037979560,2772131037&fm=26&fmt=auto&gp=0.jpg\" alt=\"图片描述\"><br><img src=\"https://pic4.zhimg.com/80/v2-5c062983ace7db9601880019190fb5a8_1440w.jpg?source=1940ef5c\" class=\"lazyload placeholder\" data-srcset=\"https://pic4.zhimg.com/80/v2-5c062983ace7db9601880019190fb5a8_1440w.jpg?source=1940ef5c\" srcset=\"https://img2.baidu.com/it/u=2037979560,2772131037&fm=26&fmt=auto&gp=0.jpg\" alt=\"图片描述\"></p>\n            </div>\n<div class=\"gallery \">\n              <p><img src=\"https://pic1.zhimg.com/80/v2-154228684029ae0c2183f65a9568c310_1440w.jpg?source=1940ef5c\" class=\"lazyload placeholder\" data-srcset=\"https://pic1.zhimg.com/80/v2-154228684029ae0c2183f65a9568c310_1440w.jpg?source=1940ef5c\" srcset=\"https://img2.baidu.com/it/u=2037979560,2772131037&fm=26&fmt=auto&gp=0.jpg\" alt=\"图片描述\"><br><img src=\"https://pic4.zhimg.com/80/v2-121618e14ad58dcedf8637127087ff27_1440w.jpg?source=1940ef5c\" class=\"lazyload placeholder\" data-srcset=\"https://pic4.zhimg.com/80/v2-121618e14ad58dcedf8637127087ff27_1440w.jpg?source=1940ef5c\" srcset=\"https://img2.baidu.com/it/u=2037979560,2772131037&fm=26&fmt=auto&gp=0.jpg\" alt=\"图片描述\"><br><img src=\"https://pic2.zhimg.com/80/v2-d61b1af36a619fec1b32775d75f4900d_1440w.jpg?source=1940ef5c\" class=\"lazyload placeholder\" data-srcset=\"https://pic2.zhimg.com/80/v2-d61b1af36a619fec1b32775d75f4900d_1440w.jpg?source=1940ef5c\" srcset=\"https://img2.baidu.com/it/u=2037979560,2772131037&fm=26&fmt=auto&gp=0.jpg\" alt=\"图片描述\"><br><img src=\"https://pic3.zhimg.com/80/v2-f94047ce45907e0966a681089835c04d_1440w.jpg?source=1940ef5c\" class=\"lazyload placeholder\" data-srcset=\"https://pic3.zhimg.com/80/v2-f94047ce45907e0966a681089835c04d_1440w.jpg?source=1940ef5c\" srcset=\"https://img2.baidu.com/it/u=2037979560,2772131037&fm=26&fmt=auto&gp=0.jpg\" alt=\"图片描述\"></p>\n            </div>\n<div class=\"gallery \">\n              <p><img src=\"https://pic4.zhimg.com/80/v2-604a15cef201cf177943af2d915eb2e7_1440w.jpg?source=1940ef5c\" class=\"lazyload placeholder\" data-srcset=\"https://pic4.zhimg.com/80/v2-604a15cef201cf177943af2d915eb2e7_1440w.jpg?source=1940ef5c\" srcset=\"https://img2.baidu.com/it/u=2037979560,2772131037&fm=26&fmt=auto&gp=0.jpg\" alt=\"图片描述\"><br><img src=\"https://pic1.zhimg.com/80/v2-bf6c555e7c61a57ba4a1fd95a9a32975_1440w.jpg?source=1940ef5c\" class=\"lazyload placeholder\" data-srcset=\"https://pic1.zhimg.com/80/v2-bf6c555e7c61a57ba4a1fd95a9a32975_1440w.jpg?source=1940ef5c\" srcset=\"https://img2.baidu.com/it/u=2037979560,2772131037&fm=26&fmt=auto&gp=0.jpg\" alt=\"图片描述\"></p>\n            </div>\n\n","site":{"data":{}},"excerpt":"","more":"<div class=\"gallery \">\n              <p><img src=\"https://pic4.zhimg.com/80/v2-5dfab6525ec92b4caf3f09e1ee72a23b_1440w.jpg?source=1940ef5c\" alt=\"图片描述\"><br><img src=\"https://pic4.zhimg.com/80/v2-5c062983ace7db9601880019190fb5a8_1440w.jpg?source=1940ef5c\" alt=\"图片描述\"></p>\n            </div>\n<div class=\"gallery \">\n              <p><img src=\"https://pic1.zhimg.com/80/v2-154228684029ae0c2183f65a9568c310_1440w.jpg?source=1940ef5c\" alt=\"图片描述\"><br><img src=\"https://pic4.zhimg.com/80/v2-121618e14ad58dcedf8637127087ff27_1440w.jpg?source=1940ef5c\" alt=\"图片描述\"><br><img src=\"https://pic2.zhimg.com/80/v2-d61b1af36a619fec1b32775d75f4900d_1440w.jpg?source=1940ef5c\" alt=\"图片描述\"><br><img src=\"https://pic3.zhimg.com/80/v2-f94047ce45907e0966a681089835c04d_1440w.jpg?source=1940ef5c\" alt=\"图片描述\"></p>\n            </div>\n<div class=\"gallery \">\n              <p><img src=\"https://pic4.zhimg.com/80/v2-604a15cef201cf177943af2d915eb2e7_1440w.jpg?source=1940ef5c\" alt=\"图片描述\"><br><img src=\"https://pic1.zhimg.com/80/v2-bf6c555e7c61a57ba4a1fd95a9a32975_1440w.jpg?source=1940ef5c\" alt=\"图片描述\"></p>\n            </div>\n\n"},{"title":"分类","date":"2021-06-19T03:07:35.000Z","type":"categories","layout":"categories","_content":"","source":"categories/index.md","raw":"---\ntitle: 分类\ndate: 2021-06-19 11:07:35\ntype: \"categories\"\nlayout: \"categories\"\n---\n","updated":"2022-01-29T06:38:28.409Z","path":"categories/index.html","comments":1,"_id":"ckyzjvxnn0006sdwocfkp9n4d","content":"","site":{"data":{}},"excerpt":"","more":""},{"title":"友情链接","date":"2022-01-29T05:59:40.000Z","onlyTitle":true,"toc":false,"_content":"\n{% issues sites | api=https://api.github.com/repos/yuang01/friends/issues?sort=updated&state=open&page=1&per_page=100&labels=active %}\n","source":"friends/index.md","raw":"---\ntitle: 友情链接\ndate: 2022-01-29 13:59:40\nonlyTitle: true # 只显示title\ntoc: false # 不显示文章目录\n---\n\n{% issues sites | api=https://api.github.com/repos/yuang01/friends/issues?sort=updated&state=open&page=1&per_page=100&labels=active %}\n","updated":"2022-01-29T06:37:26.330Z","path":"friends/index.html","comments":1,"layout":"page","_id":"ckyzjvxno0008sdwo9gu6giwd","content":"<div class=\"issues-api sites\"api=\"https://api.github.com/repos/yuang01/friends/issues?sort=updated&state=open&page=1&per_page=100&labels=active\"></div>\n","site":{"data":{}},"excerpt":"","more":"<div class=\"issues-api sites\"api=\"https://api.github.com/repos/yuang01/friends/issues?sort=updated&state=open&page=1&per_page=100&labels=active\"></div>\n"},{"title":"图库","date":"2022-01-29T06:39:04.000Z","toc":false,"img":"https://pic2.zhimg.com/80/v2-2cf3b62a87045ee279096449cf6f3ac1_1440w.jpg?source=1940ef5c","onlyTitle":true,"_content":"<div class=\"gallery-group-main\">\n    {% galleryGroup '壁纸' '收藏的一些壁纸' '/bizhi' https://pic1.zhimg.com/80/v2-23c3820e8abfb1cef689531af2dc6d09_1440w.jpg?source=1940ef5c %}\n    {% galleryGroup '古典图片' '中国古典图片' '/gudian' https://pic1.zhimg.com/80/v2-8d542d68cbbf0e5f503da9e3f72b8447_1440w.jpg?source=1940ef5c %}\n    {% galleryGroup '风景' '风景图片' '/fengjing' https://pic1.zhimg.com/80/v2-56164ef0695767475935c9e019c594ae_1440w.jpg?source=1940ef5c %}\n</div>\n","source":"gallery/index.md","raw":"---\ntitle: 图库\ndate: 2022-01-29 14:39:04\ntoc: false\nimg: https://pic2.zhimg.com/80/v2-2cf3b62a87045ee279096449cf6f3ac1_1440w.jpg?source=1940ef5c\nonlyTitle: true\n---\n<div class=\"gallery-group-main\">\n    {% galleryGroup '壁纸' '收藏的一些壁纸' '/bizhi' https://pic1.zhimg.com/80/v2-23c3820e8abfb1cef689531af2dc6d09_1440w.jpg?source=1940ef5c %}\n    {% galleryGroup '古典图片' '中国古典图片' '/gudian' https://pic1.zhimg.com/80/v2-8d542d68cbbf0e5f503da9e3f72b8447_1440w.jpg?source=1940ef5c %}\n    {% galleryGroup '风景' '风景图片' '/fengjing' https://pic1.zhimg.com/80/v2-56164ef0695767475935c9e019c594ae_1440w.jpg?source=1940ef5c %}\n</div>\n","updated":"2022-01-29T06:36:19.654Z","path":"gallery/index.html","comments":1,"layout":"page","_id":"ckyzjvxnp000asdwofwcv34jc","content":"<div class=\"gallery-group-main\">\n    \n  <figure class=\"gallery-group\">\n  <img class=\"gallery-group-img\" src='https://pic1.zhimg.com/80/v2-23c3820e8abfb1cef689531af2dc6d09_1440w.jpg?source=1940ef5c' alt=\"Group Image Gallery\">\n  <figcaption>\n  <div class=\"gallery-group-name\">壁纸</div>\n  <p>收藏的一些壁纸</p>\n  <a href='/bizhi'></a>\n  </figcaption>\n  </figure>\n  \n    \n  <figure class=\"gallery-group\">\n  <img class=\"gallery-group-img\" src='https://pic1.zhimg.com/80/v2-8d542d68cbbf0e5f503da9e3f72b8447_1440w.jpg?source=1940ef5c' alt=\"Group Image Gallery\">\n  <figcaption>\n  <div class=\"gallery-group-name\">古典图片</div>\n  <p>中国古典图片</p>\n  <a href='/gudian'></a>\n  </figcaption>\n  </figure>\n  \n    \n  <figure class=\"gallery-group\">\n  <img class=\"gallery-group-img\" src='https://pic1.zhimg.com/80/v2-56164ef0695767475935c9e019c594ae_1440w.jpg?source=1940ef5c' alt=\"Group Image Gallery\">\n  <figcaption>\n  <div class=\"gallery-group-name\">风景</div>\n  <p>风景图片</p>\n  <a href='/fengjing'></a>\n  </figcaption>\n  </figure>\n  \n</div>\n","site":{"data":{}},"excerpt":"","more":"<div class=\"gallery-group-main\">\n    \n  <figure class=\"gallery-group\">\n  <img class=\"gallery-group-img\" src='https://pic1.zhimg.com/80/v2-23c3820e8abfb1cef689531af2dc6d09_1440w.jpg?source=1940ef5c' alt=\"Group Image Gallery\">\n  <figcaption>\n  <div class=\"gallery-group-name\">壁纸</div>\n  <p>收藏的一些壁纸</p>\n  <a href='/bizhi'></a>\n  </figcaption>\n  </figure>\n  \n    \n  <figure class=\"gallery-group\">\n  <img class=\"gallery-group-img\" src='https://pic1.zhimg.com/80/v2-8d542d68cbbf0e5f503da9e3f72b8447_1440w.jpg?source=1940ef5c' alt=\"Group Image Gallery\">\n  <figcaption>\n  <div class=\"gallery-group-name\">古典图片</div>\n  <p>中国古典图片</p>\n  <a href='/gudian'></a>\n  </figcaption>\n  </figure>\n  \n    \n  <figure class=\"gallery-group\">\n  <img class=\"gallery-group-img\" src='https://pic1.zhimg.com/80/v2-56164ef0695767475935c9e019c594ae_1440w.jpg?source=1940ef5c' alt=\"Group Image Gallery\">\n  <figcaption>\n  <div class=\"gallery-group-name\">风景</div>\n  <p>风景图片</p>\n  <a href='/fengjing'></a>\n  </figcaption>\n  </figure>\n  \n</div>\n"},{"title":"标签","date":"2021-06-19T03:08:05.000Z","type":"tags","layout":"tags","_content":"","source":"tags/index.md","raw":"---\ntitle: 标签\ndate: 2021-06-19 11:08:05\ntype: \"tags\"\nlayout: \"tags\"\n---\n","updated":"2022-01-29T06:38:38.586Z","path":"tags/index.html","comments":1,"_id":"ckyzjvxnr000fsdwogdxe599g","content":"","site":{"data":{}},"excerpt":"","more":""}],"Post":[{"title":"读书大本营","date":"2021-07-03T02:44:19.000Z","_content":"\n### Distributed Algorithms: An Intuitive Approach\nDistributed Algorithms: An Intuitive Approach: Wan Fokkink: 9780262026772: Amazon.com: Books\n分布式算法书。篇幅短，介绍直白。\n在线阅读地址：https://ftp.utcluj.ro/pub/users/civan/CPD/1_RESURSE_CURS/Books/Book_2015_Fokkink_Distributed%20Algorithms.pdf\n\n### 程序员的自我修养\n《程序员的自我修养》电子书：2021-07-17——2021-07-18读完。\n\n感受较真实，评价一般。文风较朴实。\n\n### 算法图解\n《算法图解》纸质书，断断续续读了有半年之久，还没读完。。\n","source":"_posts/读书大本营.md","raw":"---\ntitle: 读书大本营\ndate: 2021-07-03 10:44:19\ntags: [读书]\ncategories: 读书大本营\n---\n\n### Distributed Algorithms: An Intuitive Approach\nDistributed Algorithms: An Intuitive Approach: Wan Fokkink: 9780262026772: Amazon.com: Books\n分布式算法书。篇幅短，介绍直白。\n在线阅读地址：https://ftp.utcluj.ro/pub/users/civan/CPD/1_RESURSE_CURS/Books/Book_2015_Fokkink_Distributed%20Algorithms.pdf\n\n### 程序员的自我修养\n《程序员的自我修养》电子书：2021-07-17——2021-07-18读完。\n\n感受较真实，评价一般。文风较朴实。\n\n### 算法图解\n《算法图解》纸质书，断断续续读了有半年之久，还没读完。。\n","slug":"读书大本营","published":1,"updated":"2022-01-28T13:15:02.941Z","comments":1,"layout":"post","photos":[],"link":"","_id":"ckyzjvxng0001sdwo7rr6frdc","content":"<h3 id=\"Distributed-Algorithms-An-Intuitive-Approach\"><a href=\"#Distributed-Algorithms-An-Intuitive-Approach\" class=\"headerlink\" title=\"Distributed Algorithms: An Intuitive Approach\"></a>Distributed Algorithms: An Intuitive Approach</h3><p>Distributed Algorithms: An Intuitive Approach: Wan Fokkink: 9780262026772: Amazon.com: Books<br>分布式算法书。篇幅短，介绍直白。<br>在线阅读地址：<a href=\"https://ftp.utcluj.ro/pub/users/civan/CPD/1_RESURSE_CURS/Books/Book_2015_Fokkink_Distributed%20Algorithms.pdf\">https://ftp.utcluj.ro/pub/users/civan/CPD/1_RESURSE_CURS/Books/Book_2015_Fokkink_Distributed%20Algorithms.pdf</a></p>\n<h3 id=\"程序员的自我修养\"><a href=\"#程序员的自我修养\" class=\"headerlink\" title=\"程序员的自我修养\"></a>程序员的自我修养</h3><p>《程序员的自我修养》电子书：2021-07-17——2021-07-18读完。</p>\n<p>感受较真实，评价一般。文风较朴实。</p>\n<h3 id=\"算法图解\"><a href=\"#算法图解\" class=\"headerlink\" title=\"算法图解\"></a>算法图解</h3><p>《算法图解》纸质书，断断续续读了有半年之久，还没读完。。</p>\n","site":{"data":{}},"excerpt":"","more":"<h3 id=\"Distributed-Algorithms-An-Intuitive-Approach\"><a href=\"#Distributed-Algorithms-An-Intuitive-Approach\" class=\"headerlink\" title=\"Distributed Algorithms: An Intuitive Approach\"></a>Distributed Algorithms: An Intuitive Approach</h3><p>Distributed Algorithms: An Intuitive Approach: Wan Fokkink: 9780262026772: Amazon.com: Books<br>分布式算法书。篇幅短，介绍直白。<br>在线阅读地址：<a href=\"https://ftp.utcluj.ro/pub/users/civan/CPD/1_RESURSE_CURS/Books/Book_2015_Fokkink_Distributed%20Algorithms.pdf\">https://ftp.utcluj.ro/pub/users/civan/CPD/1_RESURSE_CURS/Books/Book_2015_Fokkink_Distributed%20Algorithms.pdf</a></p>\n<h3 id=\"程序员的自我修养\"><a href=\"#程序员的自我修养\" class=\"headerlink\" title=\"程序员的自我修养\"></a>程序员的自我修养</h3><p>《程序员的自我修养》电子书：2021-07-17——2021-07-18读完。</p>\n<p>感受较真实，评价一般。文风较朴实。</p>\n<h3 id=\"算法图解\"><a href=\"#算法图解\" class=\"headerlink\" title=\"算法图解\"></a>算法图解</h3><p>《算法图解》纸质书，断断续续读了有半年之久，还没读完。。</p>\n"},{"title":"杂七杂八瞎捣鼓","date":"2021-07-22T15:11:30.000Z","_content":"\n### 中间件\n\n消息队列： Kafka/Rabbit MQ/Activi MQ/\n\n缓存工具：Redis\n\n### 数据库\n\nMysql/MongoDB\n\n### 服务器端语言\njava/javascript/python/golang\n\n### 前端语言\njavascript\n\n### 后端框架\nSpringCloud全家桶\n\n### 算法\n排序算法：简单排序算法、选择排序算法、冒泡排序、桶排序算法、二分查找\n\n算法思想：动态规划\n\n### 数据结构\n二叉树、树形结构、图、链表、数组、散列表\n","source":"_posts/个人随笔/杂七杂八瞎捣鼓.md","raw":"---\ntitle: 杂七杂八瞎捣鼓\ndate: 2021-07-22 23:11:30\ntags: [瞎捣鼓]\ncategories: 个人随笔\n---\n\n### 中间件\n\n消息队列： Kafka/Rabbit MQ/Activi MQ/\n\n缓存工具：Redis\n\n### 数据库\n\nMysql/MongoDB\n\n### 服务器端语言\njava/javascript/python/golang\n\n### 前端语言\njavascript\n\n### 后端框架\nSpringCloud全家桶\n\n### 算法\n排序算法：简单排序算法、选择排序算法、冒泡排序、桶排序算法、二分查找\n\n算法思想：动态规划\n\n### 数据结构\n二叉树、树形结构、图、链表、数组、散列表\n","slug":"个人随笔/杂七杂八瞎捣鼓","published":1,"updated":"2022-01-28T13:24:57.521Z","comments":1,"layout":"post","photos":[],"link":"","_id":"ckyzjvxnk0003sdwoe4ie3jrl","content":"<h3 id=\"中间件\"><a href=\"#中间件\" class=\"headerlink\" title=\"中间件\"></a>中间件</h3><p>消息队列： Kafka/Rabbit MQ/Activi MQ/</p>\n<p>缓存工具：Redis</p>\n<h3 id=\"数据库\"><a href=\"#数据库\" class=\"headerlink\" title=\"数据库\"></a>数据库</h3><p>Mysql/MongoDB</p>\n<h3 id=\"服务器端语言\"><a href=\"#服务器端语言\" class=\"headerlink\" title=\"服务器端语言\"></a>服务器端语言</h3><p>java/javascript/python/golang</p>\n<h3 id=\"前端语言\"><a href=\"#前端语言\" class=\"headerlink\" title=\"前端语言\"></a>前端语言</h3><p>javascript</p>\n<h3 id=\"后端框架\"><a href=\"#后端框架\" class=\"headerlink\" title=\"后端框架\"></a>后端框架</h3><p>SpringCloud全家桶</p>\n<h3 id=\"算法\"><a href=\"#算法\" class=\"headerlink\" title=\"算法\"></a>算法</h3><p>排序算法：简单排序算法、选择排序算法、冒泡排序、桶排序算法、二分查找</p>\n<p>算法思想：动态规划</p>\n<h3 id=\"数据结构\"><a href=\"#数据结构\" class=\"headerlink\" title=\"数据结构\"></a>数据结构</h3><p>二叉树、树形结构、图、链表、数组、散列表</p>\n","site":{"data":{}},"excerpt":"","more":"<h3 id=\"中间件\"><a href=\"#中间件\" class=\"headerlink\" title=\"中间件\"></a>中间件</h3><p>消息队列： Kafka/Rabbit MQ/Activi MQ/</p>\n<p>缓存工具：Redis</p>\n<h3 id=\"数据库\"><a href=\"#数据库\" class=\"headerlink\" title=\"数据库\"></a>数据库</h3><p>Mysql/MongoDB</p>\n<h3 id=\"服务器端语言\"><a href=\"#服务器端语言\" class=\"headerlink\" title=\"服务器端语言\"></a>服务器端语言</h3><p>java/javascript/python/golang</p>\n<h3 id=\"前端语言\"><a href=\"#前端语言\" class=\"headerlink\" title=\"前端语言\"></a>前端语言</h3><p>javascript</p>\n<h3 id=\"后端框架\"><a href=\"#后端框架\" class=\"headerlink\" title=\"后端框架\"></a>后端框架</h3><p>SpringCloud全家桶</p>\n<h3 id=\"算法\"><a href=\"#算法\" class=\"headerlink\" title=\"算法\"></a>算法</h3><p>排序算法：简单排序算法、选择排序算法、冒泡排序、桶排序算法、二分查找</p>\n<p>算法思想：动态规划</p>\n<h3 id=\"数据结构\"><a href=\"#数据结构\" class=\"headerlink\" title=\"数据结构\"></a>数据结构</h3><p>二叉树、树形结构、图、链表、数组、散列表</p>\n"},{"title":"自我高估自制力良好","date":"2021-07-20T03:11:30.000Z","_content":"\n我好像从小到大，对自我都会很高估，总是认为自己能做出来多么多么了不起的事情来，看到那些由衷敬佩的先驱者们，我有的时候在读他们的传记或者故事时，竟然会时不时的认为自己也能做出那些。心比天高，到头来发现自己什么也不是，然后又对产生能力的怀疑。我就是在这种恶性循环里长大的。很讨厌这种感觉，我有时候会问自己，这种状态是一个人该有的状态吗？会对生活或者人生起积极作用吗？\n\n看好多人都对自己进行年终总结啊，什么来年规划啊。我就学着做，上一个月，我活在每天给自己定的计划中，按计划生活，半个月前，我彻底不受控制了，一到凌晨就很嗨，脑子里心里都在给自己暗示，我白天都是在完成计划，只有现在是属于我自己时间的，尽情嗨起来吧。呵呵，觉也不愿意睡了，现在想想都很嫌弃那时的状态。\n\n要说到计划，我其实有很多计划，也对自己有很多期望，计划一旦需要坚持，我就歇菜了，我本以为自己自制力不错，可一旦进入有规律的有计划的生活，我潜意识里就会对自己说，你难道是机器人，你难道没有别的想做的事情。时间空下来准备开始完成计划的时候，总是有一个人对我说，再看会手机吧，再刷会视频吧，再推迟个几分钟再开始执行计划吧，反正计划都定好了， 晚点加快速度执行就行了。就这样，1分钟，5分钟，10分钟过去了。\n\n我是很羡慕那些自己独自一人就能更新视频，更新文章，更新技术的人的，他们独自一人的时候没有变呆变笨。\n\n原本这个时间点，我计划是。。好像没有明确定下来我现在要干什么。刚准备要鸡血起来，我发现我困了。。。一天就这样过去了。。。\n\n附一个网站链接。没想到是微软的人，看了他的随感，我内心会比较平静。\nhttps://cuiqingcai.com/\n","source":"_posts/个人随笔/自我高估自制力良好.md","raw":"---\ntitle: 自我高估自制力良好\ndate: 2021-07-20 11:11:30\ntag: [个人随笔,自制力]\ncategories: 个人随笔\n---\n\n我好像从小到大，对自我都会很高估，总是认为自己能做出来多么多么了不起的事情来，看到那些由衷敬佩的先驱者们，我有的时候在读他们的传记或者故事时，竟然会时不时的认为自己也能做出那些。心比天高，到头来发现自己什么也不是，然后又对产生能力的怀疑。我就是在这种恶性循环里长大的。很讨厌这种感觉，我有时候会问自己，这种状态是一个人该有的状态吗？会对生活或者人生起积极作用吗？\n\n看好多人都对自己进行年终总结啊，什么来年规划啊。我就学着做，上一个月，我活在每天给自己定的计划中，按计划生活，半个月前，我彻底不受控制了，一到凌晨就很嗨，脑子里心里都在给自己暗示，我白天都是在完成计划，只有现在是属于我自己时间的，尽情嗨起来吧。呵呵，觉也不愿意睡了，现在想想都很嫌弃那时的状态。\n\n要说到计划，我其实有很多计划，也对自己有很多期望，计划一旦需要坚持，我就歇菜了，我本以为自己自制力不错，可一旦进入有规律的有计划的生活，我潜意识里就会对自己说，你难道是机器人，你难道没有别的想做的事情。时间空下来准备开始完成计划的时候，总是有一个人对我说，再看会手机吧，再刷会视频吧，再推迟个几分钟再开始执行计划吧，反正计划都定好了， 晚点加快速度执行就行了。就这样，1分钟，5分钟，10分钟过去了。\n\n我是很羡慕那些自己独自一人就能更新视频，更新文章，更新技术的人的，他们独自一人的时候没有变呆变笨。\n\n原本这个时间点，我计划是。。好像没有明确定下来我现在要干什么。刚准备要鸡血起来，我发现我困了。。。一天就这样过去了。。。\n\n附一个网站链接。没想到是微软的人，看了他的随感，我内心会比较平静。\nhttps://cuiqingcai.com/\n","slug":"个人随笔/自我高估自制力良好","published":1,"updated":"2022-01-28T13:15:02.939Z","comments":1,"layout":"post","photos":[],"link":"","_id":"ckyzjvxnn0007sdwo8nb55hz8","content":"<p>我好像从小到大，对自我都会很高估，总是认为自己能做出来多么多么了不起的事情来，看到那些由衷敬佩的先驱者们，我有的时候在读他们的传记或者故事时，竟然会时不时的认为自己也能做出那些。心比天高，到头来发现自己什么也不是，然后又对产生能力的怀疑。我就是在这种恶性循环里长大的。很讨厌这种感觉，我有时候会问自己，这种状态是一个人该有的状态吗？会对生活或者人生起积极作用吗？</p>\n<p>看好多人都对自己进行年终总结啊，什么来年规划啊。我就学着做，上一个月，我活在每天给自己定的计划中，按计划生活，半个月前，我彻底不受控制了，一到凌晨就很嗨，脑子里心里都在给自己暗示，我白天都是在完成计划，只有现在是属于我自己时间的，尽情嗨起来吧。呵呵，觉也不愿意睡了，现在想想都很嫌弃那时的状态。</p>\n<p>要说到计划，我其实有很多计划，也对自己有很多期望，计划一旦需要坚持，我就歇菜了，我本以为自己自制力不错，可一旦进入有规律的有计划的生活，我潜意识里就会对自己说，你难道是机器人，你难道没有别的想做的事情。时间空下来准备开始完成计划的时候，总是有一个人对我说，再看会手机吧，再刷会视频吧，再推迟个几分钟再开始执行计划吧，反正计划都定好了， 晚点加快速度执行就行了。就这样，1分钟，5分钟，10分钟过去了。</p>\n<p>我是很羡慕那些自己独自一人就能更新视频，更新文章，更新技术的人的，他们独自一人的时候没有变呆变笨。</p>\n<p>原本这个时间点，我计划是。。好像没有明确定下来我现在要干什么。刚准备要鸡血起来，我发现我困了。。。一天就这样过去了。。。</p>\n<p>附一个网站链接。没想到是微软的人，看了他的随感，我内心会比较平静。<br><a href=\"https://cuiqingcai.com/\">https://cuiqingcai.com/</a></p>\n","site":{"data":{}},"excerpt":"","more":"<p>我好像从小到大，对自我都会很高估，总是认为自己能做出来多么多么了不起的事情来，看到那些由衷敬佩的先驱者们，我有的时候在读他们的传记或者故事时，竟然会时不时的认为自己也能做出那些。心比天高，到头来发现自己什么也不是，然后又对产生能力的怀疑。我就是在这种恶性循环里长大的。很讨厌这种感觉，我有时候会问自己，这种状态是一个人该有的状态吗？会对生活或者人生起积极作用吗？</p>\n<p>看好多人都对自己进行年终总结啊，什么来年规划啊。我就学着做，上一个月，我活在每天给自己定的计划中，按计划生活，半个月前，我彻底不受控制了，一到凌晨就很嗨，脑子里心里都在给自己暗示，我白天都是在完成计划，只有现在是属于我自己时间的，尽情嗨起来吧。呵呵，觉也不愿意睡了，现在想想都很嫌弃那时的状态。</p>\n<p>要说到计划，我其实有很多计划，也对自己有很多期望，计划一旦需要坚持，我就歇菜了，我本以为自己自制力不错，可一旦进入有规律的有计划的生活，我潜意识里就会对自己说，你难道是机器人，你难道没有别的想做的事情。时间空下来准备开始完成计划的时候，总是有一个人对我说，再看会手机吧，再刷会视频吧，再推迟个几分钟再开始执行计划吧，反正计划都定好了， 晚点加快速度执行就行了。就这样，1分钟，5分钟，10分钟过去了。</p>\n<p>我是很羡慕那些自己独自一人就能更新视频，更新文章，更新技术的人的，他们独自一人的时候没有变呆变笨。</p>\n<p>原本这个时间点，我计划是。。好像没有明确定下来我现在要干什么。刚准备要鸡血起来，我发现我困了。。。一天就这样过去了。。。</p>\n<p>附一个网站链接。没想到是微软的人，看了他的随感，我内心会比较平静。<br><a href=\"https://cuiqingcai.com/\">https://cuiqingcai.com/</a></p>\n"},{"title":"MySQL连表查询分组去重实例","date":"2021-06-27T14:48:52.000Z","_content":"\n## 业务逻辑\n通过多种渠道将小程序的活动页链接发布出去，比如通过多多种短信附带链接( channel 就记为 sms1，sms2，sms3 )，或者海报上面贴微信小程序的二维码( channel 记为 qrcode1，qrcode2，qrcode3 )，线下会员通过扫描二维码也能进入小程序指定的活动页，亦或者是通过其他会员分享的小程序链接也可以进入小程序( channel 记为 share)。这些不同的进入方式在我这篇文章统称为不同的渠道，也就是提到的 channel 字段。从不同的渠道进入活动页就会产生一条页面访问记录。会被计入 page_view 这张表里。\n\n会员进入小程序的指定活动页后，在页面上面触发一系列操作后，会得到相应的反馈，比如获得积分，或者获得优惠券等等。这步操作称为参与活动。这条数据会被记入 activity_record 这张表里。\n\n现在呢，运营小姐姐要求得到一份数据报表。每位参与活动的会员是从什么时间,哪个渠道里面进活动的？\n\n## 数据表结构\n| 表名 | member_id |participate_time|\n| --- | --- |---|\n| activity_record | 会员号 |活动参与时间|\n\n| 表名 | member_id |channel|view_time|\n| --- | --- |---|---|\n| page_view | 会员号 |渠道|页面访问时间|\n\n## 查询逻辑\n\n因为每位会员只能参加一次活动，也就是活动期间只能获得过一次积分，或者领取过一次优惠券等等这种意思，也就是每位会员最多只会产生一条 activity_record 记录。\n\n可是 page_view 这张表的记录方式就不一样了。会员可能既收到过短信链接，又扫描过活动二维码，又被好友分享过活动链接，这下，对于这位会员来说，就会产生多条页面访问记录，即在 page_view 里产生多条数据。\n\n你想想，会员肯定是先通过某一个渠道进入到活动页面，才能去参加活动。也就是有多条 page_view 的数据，按照 view_time 倒序排列，总有一条的 view_time 是小于且最接近于 activity_record 的 participate_time，下一条 page_view 的 view_time 就会大于 activity_record 的 participate_time。\n\n## SQL脚本\n```sql\nselect c.member_id,c.view_time,.channel from (\nSELECT\n\tmember_id,\n\tSUBSTRING_INDEX( GROUP_CONCAT( view_time ORDER BY view_time DESC ), ',', 1 ) AS view_time,\n\tSUBSTRING_INDEX( GROUP_CONCAT( channel ORDER BY channel DESC ), ',', 1 ) AS channel\nFROM\n\tpage_view a LEFT JOIN activity_record b\n        on a.member_id = b.member_id\n        where a.view_time < b.participate_time\nGROUP BY\n\tmember_id) c;\n```\n\n## 脚本说明\n- GROUP_CONCAT：通过使用distinct可以排除重复值； group_concat( [distinct] 要连接的字段 [order by 排序字段 asc/desc ] [separator '分隔符'] )\n- SUBSTRING_INDEX：字符串截取函数。substring_index(str,delim,count)。str:要处理的字符串；delim:分隔符；count:计数\n\n\n\n\n","source":"_posts/后端/MySQL连表查询分组去重实例.md","raw":"---\ntitle: MySQL连表查询分组去重实例\ndate: 2021-06-27 22:48:52\ntags: [MySQL]\ncategories: 后端\n---\n\n## 业务逻辑\n通过多种渠道将小程序的活动页链接发布出去，比如通过多多种短信附带链接( channel 就记为 sms1，sms2，sms3 )，或者海报上面贴微信小程序的二维码( channel 记为 qrcode1，qrcode2，qrcode3 )，线下会员通过扫描二维码也能进入小程序指定的活动页，亦或者是通过其他会员分享的小程序链接也可以进入小程序( channel 记为 share)。这些不同的进入方式在我这篇文章统称为不同的渠道，也就是提到的 channel 字段。从不同的渠道进入活动页就会产生一条页面访问记录。会被计入 page_view 这张表里。\n\n会员进入小程序的指定活动页后，在页面上面触发一系列操作后，会得到相应的反馈，比如获得积分，或者获得优惠券等等。这步操作称为参与活动。这条数据会被记入 activity_record 这张表里。\n\n现在呢，运营小姐姐要求得到一份数据报表。每位参与活动的会员是从什么时间,哪个渠道里面进活动的？\n\n## 数据表结构\n| 表名 | member_id |participate_time|\n| --- | --- |---|\n| activity_record | 会员号 |活动参与时间|\n\n| 表名 | member_id |channel|view_time|\n| --- | --- |---|---|\n| page_view | 会员号 |渠道|页面访问时间|\n\n## 查询逻辑\n\n因为每位会员只能参加一次活动，也就是活动期间只能获得过一次积分，或者领取过一次优惠券等等这种意思，也就是每位会员最多只会产生一条 activity_record 记录。\n\n可是 page_view 这张表的记录方式就不一样了。会员可能既收到过短信链接，又扫描过活动二维码，又被好友分享过活动链接，这下，对于这位会员来说，就会产生多条页面访问记录，即在 page_view 里产生多条数据。\n\n你想想，会员肯定是先通过某一个渠道进入到活动页面，才能去参加活动。也就是有多条 page_view 的数据，按照 view_time 倒序排列，总有一条的 view_time 是小于且最接近于 activity_record 的 participate_time，下一条 page_view 的 view_time 就会大于 activity_record 的 participate_time。\n\n## SQL脚本\n```sql\nselect c.member_id,c.view_time,.channel from (\nSELECT\n\tmember_id,\n\tSUBSTRING_INDEX( GROUP_CONCAT( view_time ORDER BY view_time DESC ), ',', 1 ) AS view_time,\n\tSUBSTRING_INDEX( GROUP_CONCAT( channel ORDER BY channel DESC ), ',', 1 ) AS channel\nFROM\n\tpage_view a LEFT JOIN activity_record b\n        on a.member_id = b.member_id\n        where a.view_time < b.participate_time\nGROUP BY\n\tmember_id) c;\n```\n\n## 脚本说明\n- GROUP_CONCAT：通过使用distinct可以排除重复值； group_concat( [distinct] 要连接的字段 [order by 排序字段 asc/desc ] [separator '分隔符'] )\n- SUBSTRING_INDEX：字符串截取函数。substring_index(str,delim,count)。str:要处理的字符串；delim:分隔符；count:计数\n\n\n\n\n","slug":"后端/MySQL连表查询分组去重实例","published":1,"updated":"2022-01-28T13:15:02.939Z","comments":1,"layout":"post","photos":[],"link":"","_id":"ckyzjvxno0009sdwo24r6d9uj","content":"<h2 id=\"业务逻辑\"><a href=\"#业务逻辑\" class=\"headerlink\" title=\"业务逻辑\"></a>业务逻辑</h2><p>通过多种渠道将小程序的活动页链接发布出去，比如通过多多种短信附带链接( channel 就记为 sms1，sms2，sms3 )，或者海报上面贴微信小程序的二维码( channel 记为 qrcode1，qrcode2，qrcode3 )，线下会员通过扫描二维码也能进入小程序指定的活动页，亦或者是通过其他会员分享的小程序链接也可以进入小程序( channel 记为 share)。这些不同的进入方式在我这篇文章统称为不同的渠道，也就是提到的 channel 字段。从不同的渠道进入活动页就会产生一条页面访问记录。会被计入 page_view 这张表里。</p>\n<p>会员进入小程序的指定活动页后，在页面上面触发一系列操作后，会得到相应的反馈，比如获得积分，或者获得优惠券等等。这步操作称为参与活动。这条数据会被记入 activity_record 这张表里。</p>\n<p>现在呢，运营小姐姐要求得到一份数据报表。每位参与活动的会员是从什么时间,哪个渠道里面进活动的？</p>\n<h2 id=\"数据表结构\"><a href=\"#数据表结构\" class=\"headerlink\" title=\"数据表结构\"></a>数据表结构</h2><table>\n<thead>\n<tr>\n<th>表名</th>\n<th>member_id</th>\n<th>participate_time</th>\n</tr>\n</thead>\n<tbody><tr>\n<td>activity_record</td>\n<td>会员号</td>\n<td>活动参与时间</td>\n</tr>\n</tbody></table>\n<table>\n<thead>\n<tr>\n<th>表名</th>\n<th>member_id</th>\n<th>channel</th>\n<th>view_time</th>\n</tr>\n</thead>\n<tbody><tr>\n<td>page_view</td>\n<td>会员号</td>\n<td>渠道</td>\n<td>页面访问时间</td>\n</tr>\n</tbody></table>\n<h2 id=\"查询逻辑\"><a href=\"#查询逻辑\" class=\"headerlink\" title=\"查询逻辑\"></a>查询逻辑</h2><p>因为每位会员只能参加一次活动，也就是活动期间只能获得过一次积分，或者领取过一次优惠券等等这种意思，也就是每位会员最多只会产生一条 activity_record 记录。</p>\n<p>可是 page_view 这张表的记录方式就不一样了。会员可能既收到过短信链接，又扫描过活动二维码，又被好友分享过活动链接，这下，对于这位会员来说，就会产生多条页面访问记录，即在 page_view 里产生多条数据。</p>\n<p>你想想，会员肯定是先通过某一个渠道进入到活动页面，才能去参加活动。也就是有多条 page_view 的数据，按照 view_time 倒序排列，总有一条的 view_time 是小于且最接近于 activity_record 的 participate_time，下一条 page_view 的 view_time 就会大于 activity_record 的 participate_time。</p>\n<h2 id=\"SQL脚本\"><a href=\"#SQL脚本\" class=\"headerlink\" title=\"SQL脚本\"></a>SQL脚本</h2><figure class=\"highlight sql\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"keyword\">select</span> c.member_id,c.view_time,.channel <span class=\"keyword\">from</span> (</span><br><span class=\"line\"><span class=\"keyword\">SELECT</span></span><br><span class=\"line\">\tmember_id,</span><br><span class=\"line\">\tSUBSTRING_INDEX( GROUP_CONCAT( view_time <span class=\"keyword\">ORDER</span> <span class=\"keyword\">BY</span> view_time <span class=\"keyword\">DESC</span> ), <span class=\"string\">&#x27;,&#x27;</span>, <span class=\"number\">1</span> ) <span class=\"keyword\">AS</span> view_time,</span><br><span class=\"line\">\tSUBSTRING_INDEX( GROUP_CONCAT( channel <span class=\"keyword\">ORDER</span> <span class=\"keyword\">BY</span> channel <span class=\"keyword\">DESC</span> ), <span class=\"string\">&#x27;,&#x27;</span>, <span class=\"number\">1</span> ) <span class=\"keyword\">AS</span> channel</span><br><span class=\"line\"><span class=\"keyword\">FROM</span></span><br><span class=\"line\">\tpage_view a <span class=\"keyword\">LEFT</span> <span class=\"keyword\">JOIN</span> activity_record b</span><br><span class=\"line\">        <span class=\"keyword\">on</span> a.member_id <span class=\"operator\">=</span> b.member_id</span><br><span class=\"line\">        <span class=\"keyword\">where</span> a.view_time <span class=\"operator\">&lt;</span> b.participate_time</span><br><span class=\"line\"><span class=\"keyword\">GROUP</span> <span class=\"keyword\">BY</span></span><br><span class=\"line\">\tmember_id) c;</span><br></pre></td></tr></table></figure>\n\n<h2 id=\"脚本说明\"><a href=\"#脚本说明\" class=\"headerlink\" title=\"脚本说明\"></a>脚本说明</h2><ul>\n<li>GROUP_CONCAT：通过使用distinct可以排除重复值； group_concat( [distinct] 要连接的字段 [order by 排序字段 asc/desc ] [separator ‘分隔符’] )</li>\n<li>SUBSTRING_INDEX：字符串截取函数。substring_index(str,delim,count)。str:要处理的字符串；delim:分隔符；count:计数</li>\n</ul>\n","site":{"data":{}},"excerpt":"","more":"<h2 id=\"业务逻辑\"><a href=\"#业务逻辑\" class=\"headerlink\" title=\"业务逻辑\"></a>业务逻辑</h2><p>通过多种渠道将小程序的活动页链接发布出去，比如通过多多种短信附带链接( channel 就记为 sms1，sms2，sms3 )，或者海报上面贴微信小程序的二维码( channel 记为 qrcode1，qrcode2，qrcode3 )，线下会员通过扫描二维码也能进入小程序指定的活动页，亦或者是通过其他会员分享的小程序链接也可以进入小程序( channel 记为 share)。这些不同的进入方式在我这篇文章统称为不同的渠道，也就是提到的 channel 字段。从不同的渠道进入活动页就会产生一条页面访问记录。会被计入 page_view 这张表里。</p>\n<p>会员进入小程序的指定活动页后，在页面上面触发一系列操作后，会得到相应的反馈，比如获得积分，或者获得优惠券等等。这步操作称为参与活动。这条数据会被记入 activity_record 这张表里。</p>\n<p>现在呢，运营小姐姐要求得到一份数据报表。每位参与活动的会员是从什么时间,哪个渠道里面进活动的？</p>\n<h2 id=\"数据表结构\"><a href=\"#数据表结构\" class=\"headerlink\" title=\"数据表结构\"></a>数据表结构</h2><table>\n<thead>\n<tr>\n<th>表名</th>\n<th>member_id</th>\n<th>participate_time</th>\n</tr>\n</thead>\n<tbody><tr>\n<td>activity_record</td>\n<td>会员号</td>\n<td>活动参与时间</td>\n</tr>\n</tbody></table>\n<table>\n<thead>\n<tr>\n<th>表名</th>\n<th>member_id</th>\n<th>channel</th>\n<th>view_time</th>\n</tr>\n</thead>\n<tbody><tr>\n<td>page_view</td>\n<td>会员号</td>\n<td>渠道</td>\n<td>页面访问时间</td>\n</tr>\n</tbody></table>\n<h2 id=\"查询逻辑\"><a href=\"#查询逻辑\" class=\"headerlink\" title=\"查询逻辑\"></a>查询逻辑</h2><p>因为每位会员只能参加一次活动，也就是活动期间只能获得过一次积分，或者领取过一次优惠券等等这种意思，也就是每位会员最多只会产生一条 activity_record 记录。</p>\n<p>可是 page_view 这张表的记录方式就不一样了。会员可能既收到过短信链接，又扫描过活动二维码，又被好友分享过活动链接，这下，对于这位会员来说，就会产生多条页面访问记录，即在 page_view 里产生多条数据。</p>\n<p>你想想，会员肯定是先通过某一个渠道进入到活动页面，才能去参加活动。也就是有多条 page_view 的数据，按照 view_time 倒序排列，总有一条的 view_time 是小于且最接近于 activity_record 的 participate_time，下一条 page_view 的 view_time 就会大于 activity_record 的 participate_time。</p>\n<h2 id=\"SQL脚本\"><a href=\"#SQL脚本\" class=\"headerlink\" title=\"SQL脚本\"></a>SQL脚本</h2><figure class=\"highlight sql\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"keyword\">select</span> c.member_id,c.view_time,.channel <span class=\"keyword\">from</span> (</span><br><span class=\"line\"><span class=\"keyword\">SELECT</span></span><br><span class=\"line\">\tmember_id,</span><br><span class=\"line\">\tSUBSTRING_INDEX( GROUP_CONCAT( view_time <span class=\"keyword\">ORDER</span> <span class=\"keyword\">BY</span> view_time <span class=\"keyword\">DESC</span> ), <span class=\"string\">&#x27;,&#x27;</span>, <span class=\"number\">1</span> ) <span class=\"keyword\">AS</span> view_time,</span><br><span class=\"line\">\tSUBSTRING_INDEX( GROUP_CONCAT( channel <span class=\"keyword\">ORDER</span> <span class=\"keyword\">BY</span> channel <span class=\"keyword\">DESC</span> ), <span class=\"string\">&#x27;,&#x27;</span>, <span class=\"number\">1</span> ) <span class=\"keyword\">AS</span> channel</span><br><span class=\"line\"><span class=\"keyword\">FROM</span></span><br><span class=\"line\">\tpage_view a <span class=\"keyword\">LEFT</span> <span class=\"keyword\">JOIN</span> activity_record b</span><br><span class=\"line\">        <span class=\"keyword\">on</span> a.member_id <span class=\"operator\">=</span> b.member_id</span><br><span class=\"line\">        <span class=\"keyword\">where</span> a.view_time <span class=\"operator\">&lt;</span> b.participate_time</span><br><span class=\"line\"><span class=\"keyword\">GROUP</span> <span class=\"keyword\">BY</span></span><br><span class=\"line\">\tmember_id) c;</span><br></pre></td></tr></table></figure>\n\n<h2 id=\"脚本说明\"><a href=\"#脚本说明\" class=\"headerlink\" title=\"脚本说明\"></a>脚本说明</h2><ul>\n<li>GROUP_CONCAT：通过使用distinct可以排除重复值； group_concat( [distinct] 要连接的字段 [order by 排序字段 asc/desc ] [separator ‘分隔符’] )</li>\n<li>SUBSTRING_INDEX：字符串截取函数。substring_index(str,delim,count)。str:要处理的字符串；delim:分隔符；count:计数</li>\n</ul>\n"},{"title":"redis作为缓存遇到问题点","date":"2021-08-03T14:40:52.000Z","_content":"这篇文章由一篇面试题说起。。。\n> 面试官问，如果线上redis挂了，所有请求都打到了数据库了，然后数据库也挂了。这时应该怎样恢复？\n\n## 理解\n> 如果线上 Redis 挂了。然后所有请求打到数据库导致数据库也挂了。\n\n> redis 挂了 => 缓存都没了；\n> \n> 缓存都没有了 => 缓存雪崩；\n> \n> 缓存雪崩了 => 数据库挂了；\n\n1. 缓存全没了：缓存雪崩；\n2. 缓存中没有数据库中有：缓存击穿；\n3. 缓存和数据库中都没有：缓存穿透。\n\n## 问题\nredis 挂了，为什么挂了？怎么就挂了？是不是有单点问题\n\n这就是在问 redis 服务的高可用。\n\n首先要解答 **这时该怎么进行恢复？**\n\n怎么恢复是正事，“缓存三连击”，“高可用架构”都是预防措施。答肯定要答，从事中恢复过渡到事前预防方案要自然一些。\n\n服务挂了，先把 redis 和数据库服务重新启动起来。启动之前把流量摘掉，可以先把流量拦截在入口的地方，比如简单粗暴的通过 Nginx 的配置把请求都转到精心设计的错误页面上。这样做的目的是为了防止流量过大，直接把新启动的服务，启动一个打挂一个的情况出现。\n> 要是启动起来又扛不住了，不行就价钱，加机器\n\n加机器没什么技术含量，再从缓存预热的角度往下说。\n\n当 redis 服务重新启动后，通过程序先放点已知的热点 key 进去后，系统再对外提供服务，防止缓存击穿的场景。\n\n**下面再继续说说事前预防。**\n\n## 缓存击穿\n缓存击穿是指一个请求要访问的数据，缓存中没有，但数据库中有的情况。\n\n这种情况一般来说就是缓存过期了。\n\n但是这时由于并发访问这个缓存的用户特别多，这是一个热点 key ，这么多用户的请求同时过来，在缓存里面没有取到数据，所以又同时去访问数据库取数据，引起数据库流量激增，压力瞬间增大，直接崩溃。\n\n所以一个数据有缓存，每次请求都从缓存中快速的返回了数据，但是某个时间点缓存失效了，某个请求在缓存中没有请求到数据，这时候我们就说这个请求“击穿”了缓存。针对这个场景，对应的解决方案一般来说有三种。\n\n- **第一个就是只放行一个请求到数据库，然后做构建缓存的操作。**\n借助 Redis setNX 命令设置一个标志位就行。设置成功的放行，设置失败的就轮询等待。\n\n- **第二个解决方案就是后台续命**\n这个方案的思想就是，后台开一个定时任务，专门主动更新即将过期的数据。\n\n比如程序中设置 program 这个 key 的时候，同时设置了过期时间为 10 分钟，那后台程序在第 8 分钟的时候，会去数据库查询数据并重新放到缓存中，同时再次设置缓存为10分钟。\n\n> 有种 redisson 分布式锁看门狗的原理。思想是一脉相承的。按照看门狗的思想就是每个 key （分布式锁）一个监控任务。有一定的性能消耗，所以要做取舍，不用所有 key 都做这种机制。方案落地的时候，从代码编写的角度来说麻烦些。\n\n> 运用这个思想开发一个流水号系统，思路是这样的。\n> \n> 流水号系统，属于比较关键的系统，为了降低数据库异常对服务带来的冲击，所以服务启动后就会为每种业务系统都预先在缓存中缓存5000个流水号。\n> \n> 然后后台job定时检查缓存中还剩下多少流水号，如果小于1000个，则再预先生成新的流水号，补充到缓存中，让缓存中的流水号再次回到5000个。\n> \n> 这样做的好处就是数据库异常后，至少保证还有5000个缓存可以保证上游业务，有一定的时候去恢复数据库。\n> \n> 也算是一种后台续命的思想。\n\n- **第三个方法就是：永不过期**\n结合实际场景就是这个key一定是个热点key，会有大量的请求来访问这个数据。而且这个key对应的value不会发生变化。\n\n其实上面的后台续命思想的最终体现也就是永不过期。\n\n只是后台续命的思想，会主动更新缓存，适用于缓存会变的场景。会出现缓存不一致的情况，取决于你的业务场景能接受多长时间的缓存不一致。\n\n## 缓存穿透\n缓存穿透是指一个请求要访问的数据，缓存和数据库中都没有，而用户短时间、高密度的发起这样的请求，每次都打到数据库上，给数据库造成了压力。\n\n一般来说这是恶意请求。\n\n两个方案解决\n\n第一个是缓存空对象。就是在数据库即时没有查询到数据，我们也把这次请求当作key缓存起来， value可以是null。下次同样请求就会命中这个null，缓存层就处理了这个请求，不会对数据库产生压力。\n\n这样实现起来简单，开发成本很低。这里会衍生出来一道面试题：\n> 对于恶意攻击，请求的时候key往往不相同，且只请求一次，那你要把这些key都缓存起来的话，因为每个key都只请求一次，那还是每次都会请求到数据库，没有保护到数据库。\n> \n答案是，布隆过滤器\n\n布隆过滤器的特性是说某个值存在时，这个值可能不存在。当它说不存在时，那就肯定不存在。\n\n可以基于这个特性，把已有数据都构建到布隆过滤器里面去。它可以帮忙挡住绝大部分的攻击。\n\n> 这里有个连环炮的问题：\n> 面试官：布隆过滤器容量有限且不支持删除，随着里面内容的增加，误判率就会随之上升。请求，这个问题你们是怎么解决的？\n\n也是两个答题方向。\n\n首先，不支持删除的话，就换一个支持删除的布隆过滤器的轮子，比如布谷鸟过滤器。或者就是提前重构布隆过滤器。\n\n比如在容量达到50%的时候，就申请一个新的更大的布隆过滤器来替换掉之前的过滤器。只是需要注意的是，重建你得知道有哪些数据需要进行重建的，所以你得有个地方来记录。比如就是redis、数据库，甚至内存缓存都可以。\n\n## 缓存雪崩\n缓存雪崩是指缓存中大多数的数据在同一时间到达过期时间，而查询数据量巨大，这时候，又是缓存中没有，数据库中有的情况了。\n\n和前面将的缓存击穿不同的是，缓存击穿是指大量的请求并发查询同一条数据。\n\n缓存雪崩是不同数据都到了过期时间，导致这些数据在缓存中查询不到。\n\n防止雪崩的方案简单来说就是错峰过期。\n\n在设置key过期时间的时候，再加上一个短的随机过期时间，这样就能避免大量缓存在同一时间过期，引起的缓存雪崩。\n\n## Redis 高可用架构\nRedis 高可用架构，基本上是主从、哨兵、集群这三种模式。\n\n主从结构很简单，弊端主要是出现故障的时候需要人工介入干预，需要人工介入的，就是阉割版的高可用。\n\n哨兵是官网推荐的高可用方案。接下来主要说下哨兵模式。\n\n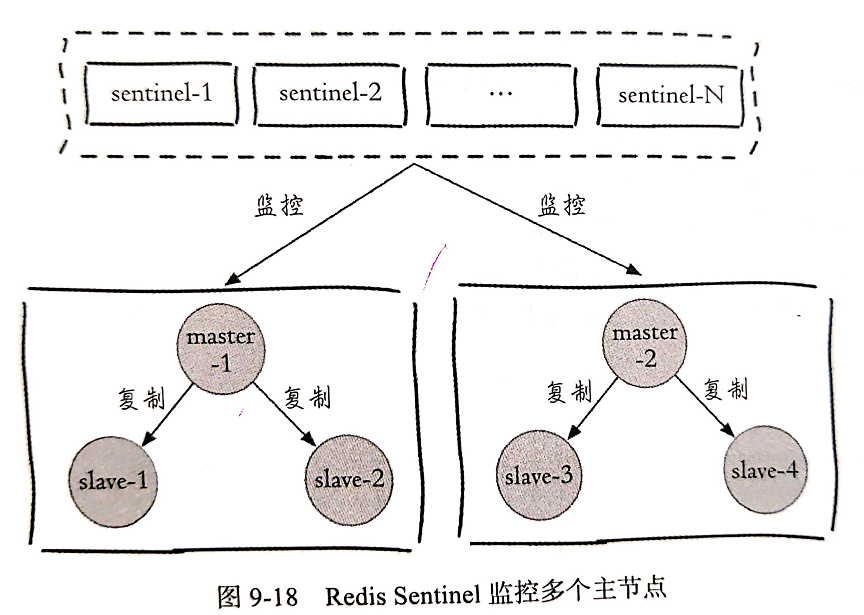![图片](https://raw.githubusercontent.com/missing-9/image-store/main/redis.jpg)\n\n\n哨兵是用来管理多个 Redis 服务的。\n\n它主要执行三种类型的任务：\n- 监控（Monitoring）：Sentinel会不断地检查你的主服务器和从服务器是否运作正常。\n- 提醒（Notification）：当被监控的某个Redis服务器出现问题时，Sentinel可以通过API向管理员或者其他应用程序发送通知。\n- 自动故障迁移（Automatic failover）：当一个主服务器不能正常工作时，Sentinel会开始一次自动故障迁移操作，它会将失效主服务器的其中一个服务器升级为新的主服务器，并让失效主服务器的其他从服务器改为复制新的主服务器；当客户端试图连接失效的主服务器时，集群也会向客户端返回新主服务器的地址，是的集群可以使用新主服务器代替失效服务器。\n\n哨兵其实也是一个分布式系统，我们可以运行多个哨兵。\n\n然后这些哨兵之间需要相互通气，交流信息，通过投票来决定是否执行自动故障迁移，以及选择哪个从服务器作为新的主服务器。\n\n另外，如果主节点挂了，哨兵到底通过什么规则选择新的主节点，也就是选举过程大致是怎么样的，也偶先面试环节。\n\n这些规则会背就完事了。\n\n- 在挂了的主节点下挂的从节点中，被标记为主观下线、已断线、或者最后一次回复 PING 命令的时间大于五秒钟的从节点都没有资格参与选举。\n- 在挂了的主节点下挂的从节点中，那些与挂了的主节点连接断开的时长超过 down-after 配置指定的时长十倍的从节点都没有资格参与选举。\n- 经过上面这两轮淘汰之后，剩下来的从服务器中，选出复制偏移量（replication offset）最大的那个从服务器作为新的主服务器。如果复制偏移量不可用，或者从服务器的复制偏移量相同，那么带有最小运行 ID 的那个从服务器成为新的主服务器。\n\n其实执行上面这些操作的，是一个哨兵。而我们的哨兵一般是三个以上，那么那个哨兵来执行这些操作呢？\n\n其实这个哨兵也是需要从多个哨兵中被选举一个出来的，被选出来的这个哨兵就是领头哨兵(leader Sentinel)。\n\n选举领头哨兵的时候，采取的是 Raft 算法。\n\n\n\n\n\n\n\n\n\n\n\n","source":"_posts/后端/redis作为缓存遇到问题点.md","raw":"---\ntitle: redis作为缓存遇到问题点\ndate: 2021-08-03 22:40:52\ntags: [redis]\ncategories: 后端\n---\n这篇文章由一篇面试题说起。。。\n> 面试官问，如果线上redis挂了，所有请求都打到了数据库了，然后数据库也挂了。这时应该怎样恢复？\n\n## 理解\n> 如果线上 Redis 挂了。然后所有请求打到数据库导致数据库也挂了。\n\n> redis 挂了 => 缓存都没了；\n> \n> 缓存都没有了 => 缓存雪崩；\n> \n> 缓存雪崩了 => 数据库挂了；\n\n1. 缓存全没了：缓存雪崩；\n2. 缓存中没有数据库中有：缓存击穿；\n3. 缓存和数据库中都没有：缓存穿透。\n\n## 问题\nredis 挂了，为什么挂了？怎么就挂了？是不是有单点问题\n\n这就是在问 redis 服务的高可用。\n\n首先要解答 **这时该怎么进行恢复？**\n\n怎么恢复是正事，“缓存三连击”，“高可用架构”都是预防措施。答肯定要答，从事中恢复过渡到事前预防方案要自然一些。\n\n服务挂了，先把 redis 和数据库服务重新启动起来。启动之前把流量摘掉，可以先把流量拦截在入口的地方，比如简单粗暴的通过 Nginx 的配置把请求都转到精心设计的错误页面上。这样做的目的是为了防止流量过大，直接把新启动的服务，启动一个打挂一个的情况出现。\n> 要是启动起来又扛不住了，不行就价钱，加机器\n\n加机器没什么技术含量，再从缓存预热的角度往下说。\n\n当 redis 服务重新启动后，通过程序先放点已知的热点 key 进去后，系统再对外提供服务，防止缓存击穿的场景。\n\n**下面再继续说说事前预防。**\n\n## 缓存击穿\n缓存击穿是指一个请求要访问的数据，缓存中没有，但数据库中有的情况。\n\n这种情况一般来说就是缓存过期了。\n\n但是这时由于并发访问这个缓存的用户特别多，这是一个热点 key ，这么多用户的请求同时过来，在缓存里面没有取到数据，所以又同时去访问数据库取数据，引起数据库流量激增，压力瞬间增大，直接崩溃。\n\n所以一个数据有缓存，每次请求都从缓存中快速的返回了数据，但是某个时间点缓存失效了，某个请求在缓存中没有请求到数据，这时候我们就说这个请求“击穿”了缓存。针对这个场景，对应的解决方案一般来说有三种。\n\n- **第一个就是只放行一个请求到数据库，然后做构建缓存的操作。**\n借助 Redis setNX 命令设置一个标志位就行。设置成功的放行，设置失败的就轮询等待。\n\n- **第二个解决方案就是后台续命**\n这个方案的思想就是，后台开一个定时任务，专门主动更新即将过期的数据。\n\n比如程序中设置 program 这个 key 的时候，同时设置了过期时间为 10 分钟，那后台程序在第 8 分钟的时候，会去数据库查询数据并重新放到缓存中，同时再次设置缓存为10分钟。\n\n> 有种 redisson 分布式锁看门狗的原理。思想是一脉相承的。按照看门狗的思想就是每个 key （分布式锁）一个监控任务。有一定的性能消耗，所以要做取舍，不用所有 key 都做这种机制。方案落地的时候，从代码编写的角度来说麻烦些。\n\n> 运用这个思想开发一个流水号系统，思路是这样的。\n> \n> 流水号系统，属于比较关键的系统，为了降低数据库异常对服务带来的冲击，所以服务启动后就会为每种业务系统都预先在缓存中缓存5000个流水号。\n> \n> 然后后台job定时检查缓存中还剩下多少流水号，如果小于1000个，则再预先生成新的流水号，补充到缓存中，让缓存中的流水号再次回到5000个。\n> \n> 这样做的好处就是数据库异常后，至少保证还有5000个缓存可以保证上游业务，有一定的时候去恢复数据库。\n> \n> 也算是一种后台续命的思想。\n\n- **第三个方法就是：永不过期**\n结合实际场景就是这个key一定是个热点key，会有大量的请求来访问这个数据。而且这个key对应的value不会发生变化。\n\n其实上面的后台续命思想的最终体现也就是永不过期。\n\n只是后台续命的思想，会主动更新缓存，适用于缓存会变的场景。会出现缓存不一致的情况，取决于你的业务场景能接受多长时间的缓存不一致。\n\n## 缓存穿透\n缓存穿透是指一个请求要访问的数据，缓存和数据库中都没有，而用户短时间、高密度的发起这样的请求，每次都打到数据库上，给数据库造成了压力。\n\n一般来说这是恶意请求。\n\n两个方案解决\n\n第一个是缓存空对象。就是在数据库即时没有查询到数据，我们也把这次请求当作key缓存起来， value可以是null。下次同样请求就会命中这个null，缓存层就处理了这个请求，不会对数据库产生压力。\n\n这样实现起来简单，开发成本很低。这里会衍生出来一道面试题：\n> 对于恶意攻击，请求的时候key往往不相同，且只请求一次，那你要把这些key都缓存起来的话，因为每个key都只请求一次，那还是每次都会请求到数据库，没有保护到数据库。\n> \n答案是，布隆过滤器\n\n布隆过滤器的特性是说某个值存在时，这个值可能不存在。当它说不存在时，那就肯定不存在。\n\n可以基于这个特性，把已有数据都构建到布隆过滤器里面去。它可以帮忙挡住绝大部分的攻击。\n\n> 这里有个连环炮的问题：\n> 面试官：布隆过滤器容量有限且不支持删除，随着里面内容的增加，误判率就会随之上升。请求，这个问题你们是怎么解决的？\n\n也是两个答题方向。\n\n首先，不支持删除的话，就换一个支持删除的布隆过滤器的轮子，比如布谷鸟过滤器。或者就是提前重构布隆过滤器。\n\n比如在容量达到50%的时候，就申请一个新的更大的布隆过滤器来替换掉之前的过滤器。只是需要注意的是，重建你得知道有哪些数据需要进行重建的，所以你得有个地方来记录。比如就是redis、数据库，甚至内存缓存都可以。\n\n## 缓存雪崩\n缓存雪崩是指缓存中大多数的数据在同一时间到达过期时间，而查询数据量巨大，这时候，又是缓存中没有，数据库中有的情况了。\n\n和前面将的缓存击穿不同的是，缓存击穿是指大量的请求并发查询同一条数据。\n\n缓存雪崩是不同数据都到了过期时间，导致这些数据在缓存中查询不到。\n\n防止雪崩的方案简单来说就是错峰过期。\n\n在设置key过期时间的时候，再加上一个短的随机过期时间，这样就能避免大量缓存在同一时间过期，引起的缓存雪崩。\n\n## Redis 高可用架构\nRedis 高可用架构，基本上是主从、哨兵、集群这三种模式。\n\n主从结构很简单，弊端主要是出现故障的时候需要人工介入干预，需要人工介入的，就是阉割版的高可用。\n\n哨兵是官网推荐的高可用方案。接下来主要说下哨兵模式。\n\n![图片](https://raw.githubusercontent.com/missing-9/image-store/main/redis.jpg)\n\n\n哨兵是用来管理多个 Redis 服务的。\n\n它主要执行三种类型的任务：\n- 监控（Monitoring）：Sentinel会不断地检查你的主服务器和从服务器是否运作正常。\n- 提醒（Notification）：当被监控的某个Redis服务器出现问题时，Sentinel可以通过API向管理员或者其他应用程序发送通知。\n- 自动故障迁移（Automatic failover）：当一个主服务器不能正常工作时，Sentinel会开始一次自动故障迁移操作，它会将失效主服务器的其中一个服务器升级为新的主服务器，并让失效主服务器的其他从服务器改为复制新的主服务器；当客户端试图连接失效的主服务器时，集群也会向客户端返回新主服务器的地址，是的集群可以使用新主服务器代替失效服务器。\n\n哨兵其实也是一个分布式系统，我们可以运行多个哨兵。\n\n然后这些哨兵之间需要相互通气，交流信息，通过投票来决定是否执行自动故障迁移，以及选择哪个从服务器作为新的主服务器。\n\n另外，如果主节点挂了，哨兵到底通过什么规则选择新的主节点，也就是选举过程大致是怎么样的，也偶先面试环节。\n\n这些规则会背就完事了。\n\n- 在挂了的主节点下挂的从节点中，被标记为主观下线、已断线、或者最后一次回复 PING 命令的时间大于五秒钟的从节点都没有资格参与选举。\n- 在挂了的主节点下挂的从节点中，那些与挂了的主节点连接断开的时长超过 down-after 配置指定的时长十倍的从节点都没有资格参与选举。\n- 经过上面这两轮淘汰之后，剩下来的从服务器中，选出复制偏移量（replication offset）最大的那个从服务器作为新的主服务器。如果复制偏移量不可用，或者从服务器的复制偏移量相同，那么带有最小运行 ID 的那个从服务器成为新的主服务器。\n\n其实执行上面这些操作的，是一个哨兵。而我们的哨兵一般是三个以上，那么那个哨兵来执行这些操作呢？\n\n其实这个哨兵也是需要从多个哨兵中被选举一个出来的，被选出来的这个哨兵就是领头哨兵(leader Sentinel)。\n\n选举领头哨兵的时候，采取的是 Raft 算法。\n\n\n\n\n\n\n\n\n\n\n\n","slug":"后端/redis作为缓存遇到问题点","published":1,"updated":"2022-01-28T13:15:02.939Z","comments":1,"layout":"post","photos":[],"link":"","_id":"ckyzjvxnq000bsdwobqxv5gr5","content":"<p>这篇文章由一篇面试题说起。。。</p>\n<blockquote>\n<p>面试官问，如果线上redis挂了，所有请求都打到了数据库了，然后数据库也挂了。这时应该怎样恢复？</p>\n</blockquote>\n<h2 id=\"理解\"><a href=\"#理解\" class=\"headerlink\" title=\"理解\"></a>理解</h2><blockquote>\n<p>如果线上 Redis 挂了。然后所有请求打到数据库导致数据库也挂了。</p>\n</blockquote>\n<blockquote>\n<p>redis 挂了 =&gt; 缓存都没了；</p>\n<p>缓存都没有了 =&gt; 缓存雪崩；</p>\n<p>缓存雪崩了 =&gt; 数据库挂了；</p>\n</blockquote>\n<ol>\n<li>缓存全没了：缓存雪崩；</li>\n<li>缓存中没有数据库中有：缓存击穿；</li>\n<li>缓存和数据库中都没有：缓存穿透。</li>\n</ol>\n<h2 id=\"问题\"><a href=\"#问题\" class=\"headerlink\" title=\"问题\"></a>问题</h2><p>redis 挂了，为什么挂了？怎么就挂了？是不是有单点问题</p>\n<p>这就是在问 redis 服务的高可用。</p>\n<p>首先要解答 <strong>这时该怎么进行恢复？</strong></p>\n<p>怎么恢复是正事，“缓存三连击”，“高可用架构”都是预防措施。答肯定要答，从事中恢复过渡到事前预防方案要自然一些。</p>\n<p>服务挂了，先把 redis 和数据库服务重新启动起来。启动之前把流量摘掉，可以先把流量拦截在入口的地方，比如简单粗暴的通过 Nginx 的配置把请求都转到精心设计的错误页面上。这样做的目的是为了防止流量过大，直接把新启动的服务，启动一个打挂一个的情况出现。</p>\n<blockquote>\n<p>要是启动起来又扛不住了，不行就价钱，加机器</p>\n</blockquote>\n<p>加机器没什么技术含量，再从缓存预热的角度往下说。</p>\n<p>当 redis 服务重新启动后，通过程序先放点已知的热点 key 进去后，系统再对外提供服务，防止缓存击穿的场景。</p>\n<p><strong>下面再继续说说事前预防。</strong></p>\n<h2 id=\"缓存击穿\"><a href=\"#缓存击穿\" class=\"headerlink\" title=\"缓存击穿\"></a>缓存击穿</h2><p>缓存击穿是指一个请求要访问的数据，缓存中没有，但数据库中有的情况。</p>\n<p>这种情况一般来说就是缓存过期了。</p>\n<p>但是这时由于并发访问这个缓存的用户特别多，这是一个热点 key ，这么多用户的请求同时过来，在缓存里面没有取到数据，所以又同时去访问数据库取数据，引起数据库流量激增，压力瞬间增大，直接崩溃。</p>\n<p>所以一个数据有缓存，每次请求都从缓存中快速的返回了数据，但是某个时间点缓存失效了，某个请求在缓存中没有请求到数据，这时候我们就说这个请求“击穿”了缓存。针对这个场景，对应的解决方案一般来说有三种。</p>\n<ul>\n<li><p><strong>第一个就是只放行一个请求到数据库，然后做构建缓存的操作。</strong><br>借助 Redis setNX 命令设置一个标志位就行。设置成功的放行，设置失败的就轮询等待。</p>\n</li>\n<li><p><strong>第二个解决方案就是后台续命</strong><br>这个方案的思想就是，后台开一个定时任务，专门主动更新即将过期的数据。</p>\n</li>\n</ul>\n<p>比如程序中设置 program 这个 key 的时候，同时设置了过期时间为 10 分钟，那后台程序在第 8 分钟的时候，会去数据库查询数据并重新放到缓存中，同时再次设置缓存为10分钟。</p>\n<blockquote>\n<p>有种 redisson 分布式锁看门狗的原理。思想是一脉相承的。按照看门狗的思想就是每个 key （分布式锁）一个监控任务。有一定的性能消耗，所以要做取舍，不用所有 key 都做这种机制。方案落地的时候，从代码编写的角度来说麻烦些。</p>\n</blockquote>\n<blockquote>\n<p>运用这个思想开发一个流水号系统，思路是这样的。</p>\n<p>流水号系统，属于比较关键的系统，为了降低数据库异常对服务带来的冲击，所以服务启动后就会为每种业务系统都预先在缓存中缓存5000个流水号。</p>\n<p>然后后台job定时检查缓存中还剩下多少流水号，如果小于1000个，则再预先生成新的流水号，补充到缓存中，让缓存中的流水号再次回到5000个。</p>\n<p>这样做的好处就是数据库异常后，至少保证还有5000个缓存可以保证上游业务，有一定的时候去恢复数据库。</p>\n<p>也算是一种后台续命的思想。</p>\n</blockquote>\n<ul>\n<li><strong>第三个方法就是：永不过期</strong><br>结合实际场景就是这个key一定是个热点key，会有大量的请求来访问这个数据。而且这个key对应的value不会发生变化。</li>\n</ul>\n<p>其实上面的后台续命思想的最终体现也就是永不过期。</p>\n<p>只是后台续命的思想，会主动更新缓存，适用于缓存会变的场景。会出现缓存不一致的情况，取决于你的业务场景能接受多长时间的缓存不一致。</p>\n<h2 id=\"缓存穿透\"><a href=\"#缓存穿透\" class=\"headerlink\" title=\"缓存穿透\"></a>缓存穿透</h2><p>缓存穿透是指一个请求要访问的数据，缓存和数据库中都没有，而用户短时间、高密度的发起这样的请求，每次都打到数据库上，给数据库造成了压力。</p>\n<p>一般来说这是恶意请求。</p>\n<p>两个方案解决</p>\n<p>第一个是缓存空对象。就是在数据库即时没有查询到数据，我们也把这次请求当作key缓存起来， value可以是null。下次同样请求就会命中这个null，缓存层就处理了这个请求，不会对数据库产生压力。</p>\n<p>这样实现起来简单，开发成本很低。这里会衍生出来一道面试题：</p>\n<blockquote>\n<p>对于恶意攻击，请求的时候key往往不相同，且只请求一次，那你要把这些key都缓存起来的话，因为每个key都只请求一次，那还是每次都会请求到数据库，没有保护到数据库。</p>\n</blockquote>\n<p>答案是，布隆过滤器</p>\n<p>布隆过滤器的特性是说某个值存在时，这个值可能不存在。当它说不存在时，那就肯定不存在。</p>\n<p>可以基于这个特性，把已有数据都构建到布隆过滤器里面去。它可以帮忙挡住绝大部分的攻击。</p>\n<blockquote>\n<p>这里有个连环炮的问题：<br>面试官：布隆过滤器容量有限且不支持删除，随着里面内容的增加，误判率就会随之上升。请求，这个问题你们是怎么解决的？</p>\n</blockquote>\n<p>也是两个答题方向。</p>\n<p>首先，不支持删除的话，就换一个支持删除的布隆过滤器的轮子，比如布谷鸟过滤器。或者就是提前重构布隆过滤器。</p>\n<p>比如在容量达到50%的时候，就申请一个新的更大的布隆过滤器来替换掉之前的过滤器。只是需要注意的是，重建你得知道有哪些数据需要进行重建的，所以你得有个地方来记录。比如就是redis、数据库，甚至内存缓存都可以。</p>\n<h2 id=\"缓存雪崩\"><a href=\"#缓存雪崩\" class=\"headerlink\" title=\"缓存雪崩\"></a>缓存雪崩</h2><p>缓存雪崩是指缓存中大多数的数据在同一时间到达过期时间，而查询数据量巨大，这时候，又是缓存中没有，数据库中有的情况了。</p>\n<p>和前面将的缓存击穿不同的是，缓存击穿是指大量的请求并发查询同一条数据。</p>\n<p>缓存雪崩是不同数据都到了过期时间，导致这些数据在缓存中查询不到。</p>\n<p>防止雪崩的方案简单来说就是错峰过期。</p>\n<p>在设置key过期时间的时候，再加上一个短的随机过期时间，这样就能避免大量缓存在同一时间过期，引起的缓存雪崩。</p>\n<h2 id=\"Redis-高可用架构\"><a href=\"#Redis-高可用架构\" class=\"headerlink\" title=\"Redis 高可用架构\"></a>Redis 高可用架构</h2><p>Redis 高可用架构，基本上是主从、哨兵、集群这三种模式。</p>\n<p>主从结构很简单，弊端主要是出现故障的时候需要人工介入干预，需要人工介入的，就是阉割版的高可用。</p>\n<p>哨兵是官网推荐的高可用方案。接下来主要说下哨兵模式。</p>\n<p><img src=\"https://raw.githubusercontent.com/missing-9/image-store/main/redis.jpg\" class=\"lazyload placeholder\" data-srcset=\"https://raw.githubusercontent.com/missing-9/image-store/main/redis.jpg\" srcset=\"https://img2.baidu.com/it/u=2037979560,2772131037&fm=26&fmt=auto&gp=0.jpg\" alt=\"图片\"></p>\n<p>哨兵是用来管理多个 Redis 服务的。</p>\n<p>它主要执行三种类型的任务：</p>\n<ul>\n<li>监控（Monitoring）：Sentinel会不断地检查你的主服务器和从服务器是否运作正常。</li>\n<li>提醒（Notification）：当被监控的某个Redis服务器出现问题时，Sentinel可以通过API向管理员或者其他应用程序发送通知。</li>\n<li>自动故障迁移（Automatic failover）：当一个主服务器不能正常工作时，Sentinel会开始一次自动故障迁移操作，它会将失效主服务器的其中一个服务器升级为新的主服务器，并让失效主服务器的其他从服务器改为复制新的主服务器；当客户端试图连接失效的主服务器时，集群也会向客户端返回新主服务器的地址，是的集群可以使用新主服务器代替失效服务器。</li>\n</ul>\n<p>哨兵其实也是一个分布式系统，我们可以运行多个哨兵。</p>\n<p>然后这些哨兵之间需要相互通气，交流信息，通过投票来决定是否执行自动故障迁移，以及选择哪个从服务器作为新的主服务器。</p>\n<p>另外，如果主节点挂了，哨兵到底通过什么规则选择新的主节点，也就是选举过程大致是怎么样的，也偶先面试环节。</p>\n<p>这些规则会背就完事了。</p>\n<ul>\n<li>在挂了的主节点下挂的从节点中，被标记为主观下线、已断线、或者最后一次回复 PING 命令的时间大于五秒钟的从节点都没有资格参与选举。</li>\n<li>在挂了的主节点下挂的从节点中，那些与挂了的主节点连接断开的时长超过 down-after 配置指定的时长十倍的从节点都没有资格参与选举。</li>\n<li>经过上面这两轮淘汰之后，剩下来的从服务器中，选出复制偏移量（replication offset）最大的那个从服务器作为新的主服务器。如果复制偏移量不可用，或者从服务器的复制偏移量相同，那么带有最小运行 ID 的那个从服务器成为新的主服务器。</li>\n</ul>\n<p>其实执行上面这些操作的，是一个哨兵。而我们的哨兵一般是三个以上，那么那个哨兵来执行这些操作呢？</p>\n<p>其实这个哨兵也是需要从多个哨兵中被选举一个出来的，被选出来的这个哨兵就是领头哨兵(leader Sentinel)。</p>\n<p>选举领头哨兵的时候，采取的是 Raft 算法。</p>\n","site":{"data":{}},"excerpt":"","more":"<p>这篇文章由一篇面试题说起。。。</p>\n<blockquote>\n<p>面试官问，如果线上redis挂了，所有请求都打到了数据库了，然后数据库也挂了。这时应该怎样恢复？</p>\n</blockquote>\n<h2 id=\"理解\"><a href=\"#理解\" class=\"headerlink\" title=\"理解\"></a>理解</h2><blockquote>\n<p>如果线上 Redis 挂了。然后所有请求打到数据库导致数据库也挂了。</p>\n</blockquote>\n<blockquote>\n<p>redis 挂了 =&gt; 缓存都没了；</p>\n<p>缓存都没有了 =&gt; 缓存雪崩；</p>\n<p>缓存雪崩了 =&gt; 数据库挂了；</p>\n</blockquote>\n<ol>\n<li>缓存全没了：缓存雪崩；</li>\n<li>缓存中没有数据库中有：缓存击穿；</li>\n<li>缓存和数据库中都没有：缓存穿透。</li>\n</ol>\n<h2 id=\"问题\"><a href=\"#问题\" class=\"headerlink\" title=\"问题\"></a>问题</h2><p>redis 挂了，为什么挂了？怎么就挂了？是不是有单点问题</p>\n<p>这就是在问 redis 服务的高可用。</p>\n<p>首先要解答 <strong>这时该怎么进行恢复？</strong></p>\n<p>怎么恢复是正事，“缓存三连击”，“高可用架构”都是预防措施。答肯定要答，从事中恢复过渡到事前预防方案要自然一些。</p>\n<p>服务挂了，先把 redis 和数据库服务重新启动起来。启动之前把流量摘掉，可以先把流量拦截在入口的地方，比如简单粗暴的通过 Nginx 的配置把请求都转到精心设计的错误页面上。这样做的目的是为了防止流量过大，直接把新启动的服务，启动一个打挂一个的情况出现。</p>\n<blockquote>\n<p>要是启动起来又扛不住了，不行就价钱，加机器</p>\n</blockquote>\n<p>加机器没什么技术含量，再从缓存预热的角度往下说。</p>\n<p>当 redis 服务重新启动后，通过程序先放点已知的热点 key 进去后，系统再对外提供服务，防止缓存击穿的场景。</p>\n<p><strong>下面再继续说说事前预防。</strong></p>\n<h2 id=\"缓存击穿\"><a href=\"#缓存击穿\" class=\"headerlink\" title=\"缓存击穿\"></a>缓存击穿</h2><p>缓存击穿是指一个请求要访问的数据，缓存中没有，但数据库中有的情况。</p>\n<p>这种情况一般来说就是缓存过期了。</p>\n<p>但是这时由于并发访问这个缓存的用户特别多，这是一个热点 key ，这么多用户的请求同时过来，在缓存里面没有取到数据，所以又同时去访问数据库取数据，引起数据库流量激增，压力瞬间增大，直接崩溃。</p>\n<p>所以一个数据有缓存，每次请求都从缓存中快速的返回了数据，但是某个时间点缓存失效了，某个请求在缓存中没有请求到数据，这时候我们就说这个请求“击穿”了缓存。针对这个场景，对应的解决方案一般来说有三种。</p>\n<ul>\n<li><p><strong>第一个就是只放行一个请求到数据库，然后做构建缓存的操作。</strong><br>借助 Redis setNX 命令设置一个标志位就行。设置成功的放行，设置失败的就轮询等待。</p>\n</li>\n<li><p><strong>第二个解决方案就是后台续命</strong><br>这个方案的思想就是，后台开一个定时任务，专门主动更新即将过期的数据。</p>\n</li>\n</ul>\n<p>比如程序中设置 program 这个 key 的时候，同时设置了过期时间为 10 分钟，那后台程序在第 8 分钟的时候，会去数据库查询数据并重新放到缓存中，同时再次设置缓存为10分钟。</p>\n<blockquote>\n<p>有种 redisson 分布式锁看门狗的原理。思想是一脉相承的。按照看门狗的思想就是每个 key （分布式锁）一个监控任务。有一定的性能消耗，所以要做取舍，不用所有 key 都做这种机制。方案落地的时候，从代码编写的角度来说麻烦些。</p>\n</blockquote>\n<blockquote>\n<p>运用这个思想开发一个流水号系统，思路是这样的。</p>\n<p>流水号系统，属于比较关键的系统，为了降低数据库异常对服务带来的冲击，所以服务启动后就会为每种业务系统都预先在缓存中缓存5000个流水号。</p>\n<p>然后后台job定时检查缓存中还剩下多少流水号，如果小于1000个，则再预先生成新的流水号，补充到缓存中，让缓存中的流水号再次回到5000个。</p>\n<p>这样做的好处就是数据库异常后，至少保证还有5000个缓存可以保证上游业务，有一定的时候去恢复数据库。</p>\n<p>也算是一种后台续命的思想。</p>\n</blockquote>\n<ul>\n<li><strong>第三个方法就是：永不过期</strong><br>结合实际场景就是这个key一定是个热点key，会有大量的请求来访问这个数据。而且这个key对应的value不会发生变化。</li>\n</ul>\n<p>其实上面的后台续命思想的最终体现也就是永不过期。</p>\n<p>只是后台续命的思想，会主动更新缓存，适用于缓存会变的场景。会出现缓存不一致的情况，取决于你的业务场景能接受多长时间的缓存不一致。</p>\n<h2 id=\"缓存穿透\"><a href=\"#缓存穿透\" class=\"headerlink\" title=\"缓存穿透\"></a>缓存穿透</h2><p>缓存穿透是指一个请求要访问的数据，缓存和数据库中都没有，而用户短时间、高密度的发起这样的请求，每次都打到数据库上，给数据库造成了压力。</p>\n<p>一般来说这是恶意请求。</p>\n<p>两个方案解决</p>\n<p>第一个是缓存空对象。就是在数据库即时没有查询到数据，我们也把这次请求当作key缓存起来， value可以是null。下次同样请求就会命中这个null，缓存层就处理了这个请求，不会对数据库产生压力。</p>\n<p>这样实现起来简单，开发成本很低。这里会衍生出来一道面试题：</p>\n<blockquote>\n<p>对于恶意攻击，请求的时候key往往不相同，且只请求一次，那你要把这些key都缓存起来的话，因为每个key都只请求一次，那还是每次都会请求到数据库，没有保护到数据库。</p>\n</blockquote>\n<p>答案是，布隆过滤器</p>\n<p>布隆过滤器的特性是说某个值存在时，这个值可能不存在。当它说不存在时，那就肯定不存在。</p>\n<p>可以基于这个特性，把已有数据都构建到布隆过滤器里面去。它可以帮忙挡住绝大部分的攻击。</p>\n<blockquote>\n<p>这里有个连环炮的问题：<br>面试官：布隆过滤器容量有限且不支持删除，随着里面内容的增加，误判率就会随之上升。请求，这个问题你们是怎么解决的？</p>\n</blockquote>\n<p>也是两个答题方向。</p>\n<p>首先，不支持删除的话，就换一个支持删除的布隆过滤器的轮子，比如布谷鸟过滤器。或者就是提前重构布隆过滤器。</p>\n<p>比如在容量达到50%的时候，就申请一个新的更大的布隆过滤器来替换掉之前的过滤器。只是需要注意的是，重建你得知道有哪些数据需要进行重建的，所以你得有个地方来记录。比如就是redis、数据库，甚至内存缓存都可以。</p>\n<h2 id=\"缓存雪崩\"><a href=\"#缓存雪崩\" class=\"headerlink\" title=\"缓存雪崩\"></a>缓存雪崩</h2><p>缓存雪崩是指缓存中大多数的数据在同一时间到达过期时间，而查询数据量巨大，这时候，又是缓存中没有，数据库中有的情况了。</p>\n<p>和前面将的缓存击穿不同的是，缓存击穿是指大量的请求并发查询同一条数据。</p>\n<p>缓存雪崩是不同数据都到了过期时间，导致这些数据在缓存中查询不到。</p>\n<p>防止雪崩的方案简单来说就是错峰过期。</p>\n<p>在设置key过期时间的时候，再加上一个短的随机过期时间，这样就能避免大量缓存在同一时间过期，引起的缓存雪崩。</p>\n<h2 id=\"Redis-高可用架构\"><a href=\"#Redis-高可用架构\" class=\"headerlink\" title=\"Redis 高可用架构\"></a>Redis 高可用架构</h2><p>Redis 高可用架构，基本上是主从、哨兵、集群这三种模式。</p>\n<p>主从结构很简单，弊端主要是出现故障的时候需要人工介入干预，需要人工介入的，就是阉割版的高可用。</p>\n<p>哨兵是官网推荐的高可用方案。接下来主要说下哨兵模式。</p>\n<p><img src=\"https://raw.githubusercontent.com/missing-9/image-store/main/redis.jpg\" alt=\"图片\"></p>\n<p>哨兵是用来管理多个 Redis 服务的。</p>\n<p>它主要执行三种类型的任务：</p>\n<ul>\n<li>监控（Monitoring）：Sentinel会不断地检查你的主服务器和从服务器是否运作正常。</li>\n<li>提醒（Notification）：当被监控的某个Redis服务器出现问题时，Sentinel可以通过API向管理员或者其他应用程序发送通知。</li>\n<li>自动故障迁移（Automatic failover）：当一个主服务器不能正常工作时，Sentinel会开始一次自动故障迁移操作，它会将失效主服务器的其中一个服务器升级为新的主服务器，并让失效主服务器的其他从服务器改为复制新的主服务器；当客户端试图连接失效的主服务器时，集群也会向客户端返回新主服务器的地址，是的集群可以使用新主服务器代替失效服务器。</li>\n</ul>\n<p>哨兵其实也是一个分布式系统，我们可以运行多个哨兵。</p>\n<p>然后这些哨兵之间需要相互通气，交流信息，通过投票来决定是否执行自动故障迁移，以及选择哪个从服务器作为新的主服务器。</p>\n<p>另外，如果主节点挂了，哨兵到底通过什么规则选择新的主节点，也就是选举过程大致是怎么样的，也偶先面试环节。</p>\n<p>这些规则会背就完事了。</p>\n<ul>\n<li>在挂了的主节点下挂的从节点中，被标记为主观下线、已断线、或者最后一次回复 PING 命令的时间大于五秒钟的从节点都没有资格参与选举。</li>\n<li>在挂了的主节点下挂的从节点中，那些与挂了的主节点连接断开的时长超过 down-after 配置指定的时长十倍的从节点都没有资格参与选举。</li>\n<li>经过上面这两轮淘汰之后，剩下来的从服务器中，选出复制偏移量（replication offset）最大的那个从服务器作为新的主服务器。如果复制偏移量不可用，或者从服务器的复制偏移量相同，那么带有最小运行 ID 的那个从服务器成为新的主服务器。</li>\n</ul>\n<p>其实执行上面这些操作的，是一个哨兵。而我们的哨兵一般是三个以上，那么那个哨兵来执行这些操作呢？</p>\n<p>其实这个哨兵也是需要从多个哨兵中被选举一个出来的，被选出来的这个哨兵就是领头哨兵(leader Sentinel)。</p>\n<p>选举领头哨兵的时候，采取的是 Raft 算法。</p>\n"},{"title":"922. 按奇偶排序数组II","date":"2021-06-19T03:50:12.000Z","_content":"\n给定一个非负整数数组 A， A 中一半整数是奇数，一半整数是偶数。\n\n对数组进行排序，以便当 A[i] 为奇数时，i 也是奇数；当 A[i] 为偶数时， i 也是偶数。\n\n你可以返回任何满足上述条件的数组作为答案。\n","source":"_posts/算法/922. 按奇偶排序数组 II.md","raw":"---\ntitle: 922. 按奇偶排序数组II\ndate: 2021-06-19 11:50:12\ntags: [算法,刷题]\ncategories: 算法\n---\n\n给定一个非负整数数组 A， A 中一半整数是奇数，一半整数是偶数。\n\n对数组进行排序，以便当 A[i] 为奇数时，i 也是奇数；当 A[i] 为偶数时， i 也是偶数。\n\n你可以返回任何满足上述条件的数组作为答案。\n","slug":"算法/922. 按奇偶排序数组 II","published":1,"updated":"2022-01-28T13:15:02.939Z","comments":1,"layout":"post","photos":[],"link":"","_id":"ckyzjvxns000gsdwo43ir46ht","content":"<p>给定一个非负整数数组 A， A 中一半整数是奇数，一半整数是偶数。</p>\n<p>对数组进行排序，以便当 A[i] 为奇数时，i 也是奇数；当 A[i] 为偶数时， i 也是偶数。</p>\n<p>你可以返回任何满足上述条件的数组作为答案。</p>\n","site":{"data":{}},"excerpt":"","more":"<p>给定一个非负整数数组 A， A 中一半整数是奇数，一半整数是偶数。</p>\n<p>对数组进行排序，以便当 A[i] 为奇数时，i 也是奇数；当 A[i] 为偶数时， i 也是偶数。</p>\n<p>你可以返回任何满足上述条件的数组作为答案。</p>\n"},{"title":"冒泡排序","date":"2021-06-19T03:13:30.000Z","_content":"\n>“冒泡排序法除了它迷人的名字和导致了某些有趣的理论问题这一事实外，似乎没有什么值得推荐的。”  ———— Donald E. Knuth（1974 年图灵奖获得者）\n\n![bubbleSort.gif](https://gitee.com/missingnine/own-image-store/raw/master/202106/bubbleSort.gif)\n\n#### 1. 基本实现\n```java\n\npublic static void main(String[] args) {\n    int[] arr = new int[]{189, -6, 0, 1, 34, 78};\n    bubbleSort2(arr);\n    Arrays.stream(arr).forEach(System.out::println);\n}\n\npublic static void bubbleSort2(int[] arr) {\n    int count=0;\n    for (int i = 0; i < arr.length - 1; i++) {\n        for (int j = 0; j < arr.length - 1 - i; j++) {\n            if (arr[j] > arr[j + 1]) {\n                swap(arr, j, j + 1);\n            }\n            count++;\n        }\n    }\n    System.out.println(\"循环进行了 \"+ count +\" 次\");\n}\n\npublic static void swap(int[] arr, int i, int j) {\n    int temp = arr[i];\n    arr[i] = arr[j];\n    arr[j] = temp;\n}\n\n\n//output\n循环进行了 15 次\n-6\n0\n1\n34\n78\n189\n\nProcess finished with exit code 0\n\n```\n#### 2. 优化版本1\n在循环遍历过程中记录了是否排过序的状态。如果某一批次中已经开始不进行排序了。就证明从头元素开始的那串剩下数组元素已经是排序正确的了。\n```java\n\npublic static void main(String[] args) {\n    int[] arr = new int[]{189, -6, 0, 1, 34, 78};\n    bubbleSort2(arr);\n    Arrays.stream(arr).forEach(System.out::println);\n}\n\npublic static void bubbleSort2(int[] arr) {\n    Boolean swaped = true;\n    for (int i = 0; i < arr.length - 1; i++) {\n        if (!swaped) {\n            break;\n        }\n        swaped = false;\n        for (int j = 0; j < arr.length - 1 - i; j++) {\n            if (arr[j] > arr[j + 1]) {\n                swap(arr, j, j + 1);\n                swaped = true;\n            }\n        }\n    }\n}\n\npublic static void swap(int[] arr, int i, int j) {\n    int temp = arr[i];\n    arr[i] = arr[j];\n    arr[j] = temp;\n}\n\n//output\n循环进行了 9 次\n-6\n0\n1\n34\n78\n189\n\nProcess finished with exit code 0\n\n```\n\n#### 3. 优化版本2\n此版本在优化版本1的基础上，再做一层优化，多引入一个变量，专门记录最后一个进行过交换的数组元素的位置。这个优化的作用是在没轮次的循环中尽可能的减少比较交换的次数。如果在某个位置之后的元素两两比较，但都没有产生过元素交换动作，那就证明从这个位置之后的元素都是有序的了。\n\n```java\npublic static void main(String[] args) {\n    int[] arr = new int[]{189, -6, 0, 1, 34, 78};\n    bubbleSort2(arr);\n    Arrays.stream(arr).forEach(System.out::println);\n}\n\npublic static void bubbleSort2(int[] arr) {\n    int count = 0;\n    boolean swapped = true;\n    int length = arr.length, lastSwappedIndex = length - 1;\n    while (swapped) {\n        swapped = false;\n        int tempLastUpdateIndex = 0;\n        for (int i = 0; i < lastSwappedIndex; i++) {\n            if (arr[i] > arr[i + 1]) {\n                swap(arr, i, i + 1);\n                swapped = true;\n                tempLastUpdateIndex = i;\n            }\n            count++;\n        }\n        lastSwappedIndex = tempLastUpdateIndex;\n    }\n    System.out.println(\"循环进行了 \" + count + \" 次\");\n}\n\npublic static void swap(int[] arr, int i, int j) {\n    int temp = arr[i];\n    arr[i] = arr[j];\n    arr[j] = temp;\n}\n\n//output\n循环进行了 9 次\n-6\n0\n1\n34\n78\n189\n\nProcess finished with exit code 0\n\n```\n","source":"_posts/算法/冒泡排序.md","raw":"---\ntitle: 冒泡排序\ndate: 2021-06-19 11:13:30\ntag: [算法,排序]\ncategories: 算法\n---\n\n>“冒泡排序法除了它迷人的名字和导致了某些有趣的理论问题这一事实外，似乎没有什么值得推荐的。”  ———— Donald E. Knuth（1974 年图灵奖获得者）\n\n![bubbleSort.gif](https://gitee.com/missingnine/own-image-store/raw/master/202106/bubbleSort.gif)\n\n#### 1. 基本实现\n```java\n\npublic static void main(String[] args) {\n    int[] arr = new int[]{189, -6, 0, 1, 34, 78};\n    bubbleSort2(arr);\n    Arrays.stream(arr).forEach(System.out::println);\n}\n\npublic static void bubbleSort2(int[] arr) {\n    int count=0;\n    for (int i = 0; i < arr.length - 1; i++) {\n        for (int j = 0; j < arr.length - 1 - i; j++) {\n            if (arr[j] > arr[j + 1]) {\n                swap(arr, j, j + 1);\n            }\n            count++;\n        }\n    }\n    System.out.println(\"循环进行了 \"+ count +\" 次\");\n}\n\npublic static void swap(int[] arr, int i, int j) {\n    int temp = arr[i];\n    arr[i] = arr[j];\n    arr[j] = temp;\n}\n\n\n//output\n循环进行了 15 次\n-6\n0\n1\n34\n78\n189\n\nProcess finished with exit code 0\n\n```\n#### 2. 优化版本1\n在循环遍历过程中记录了是否排过序的状态。如果某一批次中已经开始不进行排序了。就证明从头元素开始的那串剩下数组元素已经是排序正确的了。\n```java\n\npublic static void main(String[] args) {\n    int[] arr = new int[]{189, -6, 0, 1, 34, 78};\n    bubbleSort2(arr);\n    Arrays.stream(arr).forEach(System.out::println);\n}\n\npublic static void bubbleSort2(int[] arr) {\n    Boolean swaped = true;\n    for (int i = 0; i < arr.length - 1; i++) {\n        if (!swaped) {\n            break;\n        }\n        swaped = false;\n        for (int j = 0; j < arr.length - 1 - i; j++) {\n            if (arr[j] > arr[j + 1]) {\n                swap(arr, j, j + 1);\n                swaped = true;\n            }\n        }\n    }\n}\n\npublic static void swap(int[] arr, int i, int j) {\n    int temp = arr[i];\n    arr[i] = arr[j];\n    arr[j] = temp;\n}\n\n//output\n循环进行了 9 次\n-6\n0\n1\n34\n78\n189\n\nProcess finished with exit code 0\n\n```\n\n#### 3. 优化版本2\n此版本在优化版本1的基础上，再做一层优化，多引入一个变量，专门记录最后一个进行过交换的数组元素的位置。这个优化的作用是在没轮次的循环中尽可能的减少比较交换的次数。如果在某个位置之后的元素两两比较，但都没有产生过元素交换动作，那就证明从这个位置之后的元素都是有序的了。\n\n```java\npublic static void main(String[] args) {\n    int[] arr = new int[]{189, -6, 0, 1, 34, 78};\n    bubbleSort2(arr);\n    Arrays.stream(arr).forEach(System.out::println);\n}\n\npublic static void bubbleSort2(int[] arr) {\n    int count = 0;\n    boolean swapped = true;\n    int length = arr.length, lastSwappedIndex = length - 1;\n    while (swapped) {\n        swapped = false;\n        int tempLastUpdateIndex = 0;\n        for (int i = 0; i < lastSwappedIndex; i++) {\n            if (arr[i] > arr[i + 1]) {\n                swap(arr, i, i + 1);\n                swapped = true;\n                tempLastUpdateIndex = i;\n            }\n            count++;\n        }\n        lastSwappedIndex = tempLastUpdateIndex;\n    }\n    System.out.println(\"循环进行了 \" + count + \" 次\");\n}\n\npublic static void swap(int[] arr, int i, int j) {\n    int temp = arr[i];\n    arr[i] = arr[j];\n    arr[j] = temp;\n}\n\n//output\n循环进行了 9 次\n-6\n0\n1\n34\n78\n189\n\nProcess finished with exit code 0\n\n```\n","slug":"算法/冒泡排序","published":1,"updated":"2022-01-28T13:15:02.940Z","comments":1,"layout":"post","photos":[],"link":"","_id":"ckyzjvxnt000hsdwo8y1814v5","content":"<blockquote>\n<p>“冒泡排序法除了它迷人的名字和导致了某些有趣的理论问题这一事实外，似乎没有什么值得推荐的。”  ———— Donald E. Knuth（1974 年图灵奖获得者）</p>\n</blockquote>\n<p><img src=\"https://gitee.com/missingnine/own-image-store/raw/master/202106/bubbleSort.gif\" class=\"lazyload placeholder\" data-srcset=\"https://gitee.com/missingnine/own-image-store/raw/master/202106/bubbleSort.gif\" srcset=\"https://img2.baidu.com/it/u=2037979560,2772131037&fm=26&fmt=auto&gp=0.jpg\" alt=\"bubbleSort.gif\"></p>\n<h4 id=\"1-基本实现\"><a href=\"#1-基本实现\" class=\"headerlink\" title=\"1. 基本实现\"></a>1. 基本实现</h4><figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br><span class=\"line\">31</span><br><span class=\"line\">32</span><br><span class=\"line\">33</span><br><span class=\"line\">34</span><br><span class=\"line\">35</span><br><span class=\"line\">36</span><br><span class=\"line\">37</span><br><span class=\"line\">38</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">main</span><span class=\"params\">(String[] args)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span>[] arr = <span class=\"keyword\">new</span> <span class=\"keyword\">int</span>[]&#123;<span class=\"number\">189</span>, -<span class=\"number\">6</span>, <span class=\"number\">0</span>, <span class=\"number\">1</span>, <span class=\"number\">34</span>, <span class=\"number\">78</span>&#125;;</span><br><span class=\"line\">    bubbleSort2(arr);</span><br><span class=\"line\">    Arrays.stream(arr).forEach(System.out::println);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">bubbleSort2</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> count=<span class=\"number\">0</span>;</span><br><span class=\"line\">    <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> i = <span class=\"number\">0</span>; i &lt; arr.length - <span class=\"number\">1</span>; i++) &#123;</span><br><span class=\"line\">        <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> j = <span class=\"number\">0</span>; j &lt; arr.length - <span class=\"number\">1</span> - i; j++) &#123;</span><br><span class=\"line\">            <span class=\"keyword\">if</span> (arr[j] &gt; arr[j + <span class=\"number\">1</span>]) &#123;</span><br><span class=\"line\">                swap(arr, j, j + <span class=\"number\">1</span>);</span><br><span class=\"line\">            &#125;</span><br><span class=\"line\">            count++;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\">    System.out.println(<span class=\"string\">&quot;循环进行了 &quot;</span>+ count +<span class=\"string\">&quot; 次&quot;</span>);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">swap</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr, <span class=\"keyword\">int</span> i, <span class=\"keyword\">int</span> j)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> temp = arr[i];</span><br><span class=\"line\">    arr[i] = arr[j];</span><br><span class=\"line\">    arr[j] = temp;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"comment\">//output</span></span><br><span class=\"line\">循环进行了 <span class=\"number\">15</span> 次</span><br><span class=\"line\">-<span class=\"number\">6</span></span><br><span class=\"line\"><span class=\"number\">0</span></span><br><span class=\"line\"><span class=\"number\">1</span></span><br><span class=\"line\"><span class=\"number\">34</span></span><br><span class=\"line\"><span class=\"number\">78</span></span><br><span class=\"line\"><span class=\"number\">189</span></span><br><span class=\"line\"></span><br><span class=\"line\">Process finished with exit code <span class=\"number\">0</span></span><br><span class=\"line\"></span><br></pre></td></tr></table></figure>\n<h4 id=\"2-优化版本1\"><a href=\"#2-优化版本1\" class=\"headerlink\" title=\"2. 优化版本1\"></a>2. 优化版本1</h4><p>在循环遍历过程中记录了是否排过序的状态。如果某一批次中已经开始不进行排序了。就证明从头元素开始的那串剩下数组元素已经是排序正确的了。</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br><span class=\"line\">31</span><br><span class=\"line\">32</span><br><span class=\"line\">33</span><br><span class=\"line\">34</span><br><span class=\"line\">35</span><br><span class=\"line\">36</span><br><span class=\"line\">37</span><br><span class=\"line\">38</span><br><span class=\"line\">39</span><br><span class=\"line\">40</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">main</span><span class=\"params\">(String[] args)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span>[] arr = <span class=\"keyword\">new</span> <span class=\"keyword\">int</span>[]&#123;<span class=\"number\">189</span>, -<span class=\"number\">6</span>, <span class=\"number\">0</span>, <span class=\"number\">1</span>, <span class=\"number\">34</span>, <span class=\"number\">78</span>&#125;;</span><br><span class=\"line\">    bubbleSort2(arr);</span><br><span class=\"line\">    Arrays.stream(arr).forEach(System.out::println);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">bubbleSort2</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr)</span> </span>&#123;</span><br><span class=\"line\">    Boolean swaped = <span class=\"keyword\">true</span>;</span><br><span class=\"line\">    <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> i = <span class=\"number\">0</span>; i &lt; arr.length - <span class=\"number\">1</span>; i++) &#123;</span><br><span class=\"line\">        <span class=\"keyword\">if</span> (!swaped) &#123;</span><br><span class=\"line\">            <span class=\"keyword\">break</span>;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">        swaped = <span class=\"keyword\">false</span>;</span><br><span class=\"line\">        <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> j = <span class=\"number\">0</span>; j &lt; arr.length - <span class=\"number\">1</span> - i; j++) &#123;</span><br><span class=\"line\">            <span class=\"keyword\">if</span> (arr[j] &gt; arr[j + <span class=\"number\">1</span>]) &#123;</span><br><span class=\"line\">                swap(arr, j, j + <span class=\"number\">1</span>);</span><br><span class=\"line\">                swaped = <span class=\"keyword\">true</span>;</span><br><span class=\"line\">            &#125;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">swap</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr, <span class=\"keyword\">int</span> i, <span class=\"keyword\">int</span> j)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> temp = arr[i];</span><br><span class=\"line\">    arr[i] = arr[j];</span><br><span class=\"line\">    arr[j] = temp;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"comment\">//output</span></span><br><span class=\"line\">循环进行了 <span class=\"number\">9</span> 次</span><br><span class=\"line\">-<span class=\"number\">6</span></span><br><span class=\"line\"><span class=\"number\">0</span></span><br><span class=\"line\"><span class=\"number\">1</span></span><br><span class=\"line\"><span class=\"number\">34</span></span><br><span class=\"line\"><span class=\"number\">78</span></span><br><span class=\"line\"><span class=\"number\">189</span></span><br><span class=\"line\"></span><br><span class=\"line\">Process finished with exit code <span class=\"number\">0</span></span><br><span class=\"line\"></span><br></pre></td></tr></table></figure>\n\n<h4 id=\"3-优化版本2\"><a href=\"#3-优化版本2\" class=\"headerlink\" title=\"3. 优化版本2\"></a>3. 优化版本2</h4><p>此版本在优化版本1的基础上，再做一层优化，多引入一个变量，专门记录最后一个进行过交换的数组元素的位置。这个优化的作用是在没轮次的循环中尽可能的减少比较交换的次数。如果在某个位置之后的元素两两比较，但都没有产生过元素交换动作，那就证明从这个位置之后的元素都是有序的了。</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br><span class=\"line\">31</span><br><span class=\"line\">32</span><br><span class=\"line\">33</span><br><span class=\"line\">34</span><br><span class=\"line\">35</span><br><span class=\"line\">36</span><br><span class=\"line\">37</span><br><span class=\"line\">38</span><br><span class=\"line\">39</span><br><span class=\"line\">40</span><br><span class=\"line\">41</span><br><span class=\"line\">42</span><br><span class=\"line\">43</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">main</span><span class=\"params\">(String[] args)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span>[] arr = <span class=\"keyword\">new</span> <span class=\"keyword\">int</span>[]&#123;<span class=\"number\">189</span>, -<span class=\"number\">6</span>, <span class=\"number\">0</span>, <span class=\"number\">1</span>, <span class=\"number\">34</span>, <span class=\"number\">78</span>&#125;;</span><br><span class=\"line\">    bubbleSort2(arr);</span><br><span class=\"line\">    Arrays.stream(arr).forEach(System.out::println);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">bubbleSort2</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> count = <span class=\"number\">0</span>;</span><br><span class=\"line\">    <span class=\"keyword\">boolean</span> swapped = <span class=\"keyword\">true</span>;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> length = arr.length, lastSwappedIndex = length - <span class=\"number\">1</span>;</span><br><span class=\"line\">    <span class=\"keyword\">while</span> (swapped) &#123;</span><br><span class=\"line\">        swapped = <span class=\"keyword\">false</span>;</span><br><span class=\"line\">        <span class=\"keyword\">int</span> tempLastUpdateIndex = <span class=\"number\">0</span>;</span><br><span class=\"line\">        <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> i = <span class=\"number\">0</span>; i &lt; lastSwappedIndex; i++) &#123;</span><br><span class=\"line\">            <span class=\"keyword\">if</span> (arr[i] &gt; arr[i + <span class=\"number\">1</span>]) &#123;</span><br><span class=\"line\">                swap(arr, i, i + <span class=\"number\">1</span>);</span><br><span class=\"line\">                swapped = <span class=\"keyword\">true</span>;</span><br><span class=\"line\">                tempLastUpdateIndex = i;</span><br><span class=\"line\">            &#125;</span><br><span class=\"line\">            count++;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">        lastSwappedIndex = tempLastUpdateIndex;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\">    System.out.println(<span class=\"string\">&quot;循环进行了 &quot;</span> + count + <span class=\"string\">&quot; 次&quot;</span>);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">swap</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr, <span class=\"keyword\">int</span> i, <span class=\"keyword\">int</span> j)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> temp = arr[i];</span><br><span class=\"line\">    arr[i] = arr[j];</span><br><span class=\"line\">    arr[j] = temp;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"comment\">//output</span></span><br><span class=\"line\">循环进行了 <span class=\"number\">9</span> 次</span><br><span class=\"line\">-<span class=\"number\">6</span></span><br><span class=\"line\"><span class=\"number\">0</span></span><br><span class=\"line\"><span class=\"number\">1</span></span><br><span class=\"line\"><span class=\"number\">34</span></span><br><span class=\"line\"><span class=\"number\">78</span></span><br><span class=\"line\"><span class=\"number\">189</span></span><br><span class=\"line\"></span><br><span class=\"line\">Process finished with exit code <span class=\"number\">0</span></span><br><span class=\"line\"></span><br></pre></td></tr></table></figure>\n","site":{"data":{}},"excerpt":"","more":"<blockquote>\n<p>“冒泡排序法除了它迷人的名字和导致了某些有趣的理论问题这一事实外，似乎没有什么值得推荐的。”  ———— Donald E. Knuth（1974 年图灵奖获得者）</p>\n</blockquote>\n<p><img src=\"https://gitee.com/missingnine/own-image-store/raw/master/202106/bubbleSort.gif\" alt=\"bubbleSort.gif\"></p>\n<h4 id=\"1-基本实现\"><a href=\"#1-基本实现\" class=\"headerlink\" title=\"1. 基本实现\"></a>1. 基本实现</h4><figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br><span class=\"line\">31</span><br><span class=\"line\">32</span><br><span class=\"line\">33</span><br><span class=\"line\">34</span><br><span class=\"line\">35</span><br><span class=\"line\">36</span><br><span class=\"line\">37</span><br><span class=\"line\">38</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">main</span><span class=\"params\">(String[] args)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span>[] arr = <span class=\"keyword\">new</span> <span class=\"keyword\">int</span>[]&#123;<span class=\"number\">189</span>, -<span class=\"number\">6</span>, <span class=\"number\">0</span>, <span class=\"number\">1</span>, <span class=\"number\">34</span>, <span class=\"number\">78</span>&#125;;</span><br><span class=\"line\">    bubbleSort2(arr);</span><br><span class=\"line\">    Arrays.stream(arr).forEach(System.out::println);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">bubbleSort2</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> count=<span class=\"number\">0</span>;</span><br><span class=\"line\">    <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> i = <span class=\"number\">0</span>; i &lt; arr.length - <span class=\"number\">1</span>; i++) &#123;</span><br><span class=\"line\">        <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> j = <span class=\"number\">0</span>; j &lt; arr.length - <span class=\"number\">1</span> - i; j++) &#123;</span><br><span class=\"line\">            <span class=\"keyword\">if</span> (arr[j] &gt; arr[j + <span class=\"number\">1</span>]) &#123;</span><br><span class=\"line\">                swap(arr, j, j + <span class=\"number\">1</span>);</span><br><span class=\"line\">            &#125;</span><br><span class=\"line\">            count++;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\">    System.out.println(<span class=\"string\">&quot;循环进行了 &quot;</span>+ count +<span class=\"string\">&quot; 次&quot;</span>);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">swap</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr, <span class=\"keyword\">int</span> i, <span class=\"keyword\">int</span> j)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> temp = arr[i];</span><br><span class=\"line\">    arr[i] = arr[j];</span><br><span class=\"line\">    arr[j] = temp;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"comment\">//output</span></span><br><span class=\"line\">循环进行了 <span class=\"number\">15</span> 次</span><br><span class=\"line\">-<span class=\"number\">6</span></span><br><span class=\"line\"><span class=\"number\">0</span></span><br><span class=\"line\"><span class=\"number\">1</span></span><br><span class=\"line\"><span class=\"number\">34</span></span><br><span class=\"line\"><span class=\"number\">78</span></span><br><span class=\"line\"><span class=\"number\">189</span></span><br><span class=\"line\"></span><br><span class=\"line\">Process finished with exit code <span class=\"number\">0</span></span><br><span class=\"line\"></span><br></pre></td></tr></table></figure>\n<h4 id=\"2-优化版本1\"><a href=\"#2-优化版本1\" class=\"headerlink\" title=\"2. 优化版本1\"></a>2. 优化版本1</h4><p>在循环遍历过程中记录了是否排过序的状态。如果某一批次中已经开始不进行排序了。就证明从头元素开始的那串剩下数组元素已经是排序正确的了。</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br><span class=\"line\">31</span><br><span class=\"line\">32</span><br><span class=\"line\">33</span><br><span class=\"line\">34</span><br><span class=\"line\">35</span><br><span class=\"line\">36</span><br><span class=\"line\">37</span><br><span class=\"line\">38</span><br><span class=\"line\">39</span><br><span class=\"line\">40</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">main</span><span class=\"params\">(String[] args)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span>[] arr = <span class=\"keyword\">new</span> <span class=\"keyword\">int</span>[]&#123;<span class=\"number\">189</span>, -<span class=\"number\">6</span>, <span class=\"number\">0</span>, <span class=\"number\">1</span>, <span class=\"number\">34</span>, <span class=\"number\">78</span>&#125;;</span><br><span class=\"line\">    bubbleSort2(arr);</span><br><span class=\"line\">    Arrays.stream(arr).forEach(System.out::println);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">bubbleSort2</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr)</span> </span>&#123;</span><br><span class=\"line\">    Boolean swaped = <span class=\"keyword\">true</span>;</span><br><span class=\"line\">    <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> i = <span class=\"number\">0</span>; i &lt; arr.length - <span class=\"number\">1</span>; i++) &#123;</span><br><span class=\"line\">        <span class=\"keyword\">if</span> (!swaped) &#123;</span><br><span class=\"line\">            <span class=\"keyword\">break</span>;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">        swaped = <span class=\"keyword\">false</span>;</span><br><span class=\"line\">        <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> j = <span class=\"number\">0</span>; j &lt; arr.length - <span class=\"number\">1</span> - i; j++) &#123;</span><br><span class=\"line\">            <span class=\"keyword\">if</span> (arr[j] &gt; arr[j + <span class=\"number\">1</span>]) &#123;</span><br><span class=\"line\">                swap(arr, j, j + <span class=\"number\">1</span>);</span><br><span class=\"line\">                swaped = <span class=\"keyword\">true</span>;</span><br><span class=\"line\">            &#125;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">swap</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr, <span class=\"keyword\">int</span> i, <span class=\"keyword\">int</span> j)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> temp = arr[i];</span><br><span class=\"line\">    arr[i] = arr[j];</span><br><span class=\"line\">    arr[j] = temp;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"comment\">//output</span></span><br><span class=\"line\">循环进行了 <span class=\"number\">9</span> 次</span><br><span class=\"line\">-<span class=\"number\">6</span></span><br><span class=\"line\"><span class=\"number\">0</span></span><br><span class=\"line\"><span class=\"number\">1</span></span><br><span class=\"line\"><span class=\"number\">34</span></span><br><span class=\"line\"><span class=\"number\">78</span></span><br><span class=\"line\"><span class=\"number\">189</span></span><br><span class=\"line\"></span><br><span class=\"line\">Process finished with exit code <span class=\"number\">0</span></span><br><span class=\"line\"></span><br></pre></td></tr></table></figure>\n\n<h4 id=\"3-优化版本2\"><a href=\"#3-优化版本2\" class=\"headerlink\" title=\"3. 优化版本2\"></a>3. 优化版本2</h4><p>此版本在优化版本1的基础上，再做一层优化，多引入一个变量，专门记录最后一个进行过交换的数组元素的位置。这个优化的作用是在没轮次的循环中尽可能的减少比较交换的次数。如果在某个位置之后的元素两两比较，但都没有产生过元素交换动作，那就证明从这个位置之后的元素都是有序的了。</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br><span class=\"line\">31</span><br><span class=\"line\">32</span><br><span class=\"line\">33</span><br><span class=\"line\">34</span><br><span class=\"line\">35</span><br><span class=\"line\">36</span><br><span class=\"line\">37</span><br><span class=\"line\">38</span><br><span class=\"line\">39</span><br><span class=\"line\">40</span><br><span class=\"line\">41</span><br><span class=\"line\">42</span><br><span class=\"line\">43</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">main</span><span class=\"params\">(String[] args)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span>[] arr = <span class=\"keyword\">new</span> <span class=\"keyword\">int</span>[]&#123;<span class=\"number\">189</span>, -<span class=\"number\">6</span>, <span class=\"number\">0</span>, <span class=\"number\">1</span>, <span class=\"number\">34</span>, <span class=\"number\">78</span>&#125;;</span><br><span class=\"line\">    bubbleSort2(arr);</span><br><span class=\"line\">    Arrays.stream(arr).forEach(System.out::println);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">bubbleSort2</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> count = <span class=\"number\">0</span>;</span><br><span class=\"line\">    <span class=\"keyword\">boolean</span> swapped = <span class=\"keyword\">true</span>;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> length = arr.length, lastSwappedIndex = length - <span class=\"number\">1</span>;</span><br><span class=\"line\">    <span class=\"keyword\">while</span> (swapped) &#123;</span><br><span class=\"line\">        swapped = <span class=\"keyword\">false</span>;</span><br><span class=\"line\">        <span class=\"keyword\">int</span> tempLastUpdateIndex = <span class=\"number\">0</span>;</span><br><span class=\"line\">        <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> i = <span class=\"number\">0</span>; i &lt; lastSwappedIndex; i++) &#123;</span><br><span class=\"line\">            <span class=\"keyword\">if</span> (arr[i] &gt; arr[i + <span class=\"number\">1</span>]) &#123;</span><br><span class=\"line\">                swap(arr, i, i + <span class=\"number\">1</span>);</span><br><span class=\"line\">                swapped = <span class=\"keyword\">true</span>;</span><br><span class=\"line\">                tempLastUpdateIndex = i;</span><br><span class=\"line\">            &#125;</span><br><span class=\"line\">            count++;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">        lastSwappedIndex = tempLastUpdateIndex;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\">    System.out.println(<span class=\"string\">&quot;循环进行了 &quot;</span> + count + <span class=\"string\">&quot; 次&quot;</span>);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">swap</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr, <span class=\"keyword\">int</span> i, <span class=\"keyword\">int</span> j)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> temp = arr[i];</span><br><span class=\"line\">    arr[i] = arr[j];</span><br><span class=\"line\">    arr[j] = temp;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"comment\">//output</span></span><br><span class=\"line\">循环进行了 <span class=\"number\">9</span> 次</span><br><span class=\"line\">-<span class=\"number\">6</span></span><br><span class=\"line\"><span class=\"number\">0</span></span><br><span class=\"line\"><span class=\"number\">1</span></span><br><span class=\"line\"><span class=\"number\">34</span></span><br><span class=\"line\"><span class=\"number\">78</span></span><br><span class=\"line\"><span class=\"number\">189</span></span><br><span class=\"line\"></span><br><span class=\"line\">Process finished with exit code <span class=\"number\">0</span></span><br><span class=\"line\"></span><br></pre></td></tr></table></figure>\n"},{"title":"回溯算法实战系列之全排列问题","date":"2021-06-27T14:51:19.000Z","_content":"\n### 题目实例Ⅰ\n\n**784. 字母大小写全排列**\n\n给定一个字符串S，通过将字符串S中的每个字母转变大小写，我们可以获得一个新的字符串。返回所有可能得到的字符串集合。\n\n示例 1：\n> 输入：S = \"a1b2\"\n>\n> 输出：[\"a1b2\", \"a1B2\", \"A1b2\", \"A1B2\"]\n\n示例 2：\n> 输入：S = \"3z4\"\n>\n> 输出：[\"3z4\", \"3Z4\"]\n\n示例 3：\n> 输入：S = \"12345\"\n>\n> 输出：[\"12345\"]\n\n提示：\n- S 的长度不超过12。\n- S 仅由数字和字母组成。\n\n友情链接：https://leetcode-cn.com/problems/letter-case-permutation/\n\n### 代码实战Ⅰ\n```java\nclass Solution {\n    StringBuilder path = new StringBuilder();\n    public List<String> letterCasePermutation(String s) {\n        ArrayList<String> res = new ArrayList<>();\n        backTracking(s, res, 0);\n        return res;\n    }\n\n    public void backTracking(String s, ArrayList<String> res, int index) {\n        if (path.length() == s.length()) {\n            res.add(new String(path.toString()));\n            return;\n        }\n\n        for (int i = index; i < s.length(); i++) {\n            char ch = s.charAt(i);\n            if (Character.isDigit(ch)) {\n                path.append(ch);\n                backTracking(s, res, i + 1);\n                path.deleteCharAt(path.length() - 1);\n            } else {\n                path.append(Character.toLowerCase(ch));\n                backTracking(s, res, i + 1);\n                path.deleteCharAt(path.length() - 1);\n\n                path.append(Character.toUpperCase(ch));\n                backTracking(s, res, i + 1);\n                path.deleteCharAt(path.length() - 1);\n            }\n        }\n    }\n}\n\n```\n\n![image.png](https://p6-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/93356abf8c074eccac4688a4806df115~tplv-k3u1fbpfcp-watermark.image)\n\n\n### 题目实例Ⅱ\n\n**47. 全排列 II**\n\n给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。\n\n示例 1：\n> 输入：nums = [1,1,2]\n>\n> 输出：\n>\n> [[1,1,2],\n>\n> [1,2,1],\n>\n> [2,1,1]]\n\n示例 2：\n> 输入：nums = [1,2,3]\n>\n> 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]\n\n提示：\n- 1 <= nums.length <= 8\n- -10 <= nums[i] <= 10\n\n友情链接：https://leetcode-cn.com/problems/permutations-ii/\n\n### 代码实战Ⅱ\n```java\nclass Solution {\n    public List<List<Integer>> permuteUnique(int[] nums) {\n        List<List<Integer>> res = new ArrayList<>();\n        LinkedList<Integer> path = new LinkedList<>();\n        int depth = 0;\n        Arrays.sort(nums);\n        boolean[] used = new boolean[nums.length];\n        backTracking(nums, used, path, depth, res);\n        return res;\n    }\n\n    public static void backTracking(int[] nums, boolean[] used, LinkedList<Integer> path, int depth, List<List<Integer>> res) {\n        if (nums.length == depth) {\n            res.add(new ArrayList<>(path));\n            return;\n        }\n        for (int i = 0; i < nums.length; i++) {\n            if (!used[i]) {\n                if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {\n                    continue;\n                }\n                path.add(nums[i]);\n                used[i] = true;\n                backTracking(nums, used, path, depth + 1, res);\n                used[i] = false;\n                path.removeLast();\n            }\n        }\n    }\n}\n```\n\n\n![image.png](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/31d9faf5dea64c96934295a1ae01029f~tplv-k3u1fbpfcp-watermark.image)\n","source":"_posts/算法/回溯算法实战系列之全排列问题.md","raw":"---\ntitle: 回溯算法实战系列之全排列问题\ndate: 2021-06-27 22:51:19\ntags: [算法,回溯算法]\ncategories: 算法\n---\n\n### 题目实例Ⅰ\n\n**784. 字母大小写全排列**\n\n给定一个字符串S，通过将字符串S中的每个字母转变大小写，我们可以获得一个新的字符串。返回所有可能得到的字符串集合。\n\n示例 1：\n> 输入：S = \"a1b2\"\n>\n> 输出：[\"a1b2\", \"a1B2\", \"A1b2\", \"A1B2\"]\n\n示例 2：\n> 输入：S = \"3z4\"\n>\n> 输出：[\"3z4\", \"3Z4\"]\n\n示例 3：\n> 输入：S = \"12345\"\n>\n> 输出：[\"12345\"]\n\n提示：\n- S 的长度不超过12。\n- S 仅由数字和字母组成。\n\n友情链接：https://leetcode-cn.com/problems/letter-case-permutation/\n\n### 代码实战Ⅰ\n```java\nclass Solution {\n    StringBuilder path = new StringBuilder();\n    public List<String> letterCasePermutation(String s) {\n        ArrayList<String> res = new ArrayList<>();\n        backTracking(s, res, 0);\n        return res;\n    }\n\n    public void backTracking(String s, ArrayList<String> res, int index) {\n        if (path.length() == s.length()) {\n            res.add(new String(path.toString()));\n            return;\n        }\n\n        for (int i = index; i < s.length(); i++) {\n            char ch = s.charAt(i);\n            if (Character.isDigit(ch)) {\n                path.append(ch);\n                backTracking(s, res, i + 1);\n                path.deleteCharAt(path.length() - 1);\n            } else {\n                path.append(Character.toLowerCase(ch));\n                backTracking(s, res, i + 1);\n                path.deleteCharAt(path.length() - 1);\n\n                path.append(Character.toUpperCase(ch));\n                backTracking(s, res, i + 1);\n                path.deleteCharAt(path.length() - 1);\n            }\n        }\n    }\n}\n\n```\n\n![image.png](https://p6-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/93356abf8c074eccac4688a4806df115~tplv-k3u1fbpfcp-watermark.image)\n\n\n### 题目实例Ⅱ\n\n**47. 全排列 II**\n\n给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。\n\n示例 1：\n> 输入：nums = [1,1,2]\n>\n> 输出：\n>\n> [[1,1,2],\n>\n> [1,2,1],\n>\n> [2,1,1]]\n\n示例 2：\n> 输入：nums = [1,2,3]\n>\n> 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]\n\n提示：\n- 1 <= nums.length <= 8\n- -10 <= nums[i] <= 10\n\n友情链接：https://leetcode-cn.com/problems/permutations-ii/\n\n### 代码实战Ⅱ\n```java\nclass Solution {\n    public List<List<Integer>> permuteUnique(int[] nums) {\n        List<List<Integer>> res = new ArrayList<>();\n        LinkedList<Integer> path = new LinkedList<>();\n        int depth = 0;\n        Arrays.sort(nums);\n        boolean[] used = new boolean[nums.length];\n        backTracking(nums, used, path, depth, res);\n        return res;\n    }\n\n    public static void backTracking(int[] nums, boolean[] used, LinkedList<Integer> path, int depth, List<List<Integer>> res) {\n        if (nums.length == depth) {\n            res.add(new ArrayList<>(path));\n            return;\n        }\n        for (int i = 0; i < nums.length; i++) {\n            if (!used[i]) {\n                if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {\n                    continue;\n                }\n                path.add(nums[i]);\n                used[i] = true;\n                backTracking(nums, used, path, depth + 1, res);\n                used[i] = false;\n                path.removeLast();\n            }\n        }\n    }\n}\n```\n\n\n![image.png](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/31d9faf5dea64c96934295a1ae01029f~tplv-k3u1fbpfcp-watermark.image)\n","slug":"算法/回溯算法实战系列之全排列问题","published":1,"updated":"2022-01-28T13:15:02.940Z","comments":1,"layout":"post","photos":[],"link":"","_id":"ckyzjvxnx000lsdwo5mvyhu6i","content":"<h3 id=\"题目实例Ⅰ\"><a href=\"#题目实例Ⅰ\" class=\"headerlink\" title=\"题目实例Ⅰ\"></a>题目实例Ⅰ</h3><p><strong>784. 字母大小写全排列</strong></p>\n<p>给定一个字符串S，通过将字符串S中的每个字母转变大小写，我们可以获得一个新的字符串。返回所有可能得到的字符串集合。</p>\n<p>示例 1：</p>\n<blockquote>\n<p>输入：S = “a1b2”</p>\n<p>输出：[“a1b2”, “a1B2”, “A1b2”, “A1B2”]</p>\n</blockquote>\n<p>示例 2：</p>\n<blockquote>\n<p>输入：S = “3z4”</p>\n<p>输出：[“3z4”, “3Z4”]</p>\n</blockquote>\n<p>示例 3：</p>\n<blockquote>\n<p>输入：S = “12345”</p>\n<p>输出：[“12345”]</p>\n</blockquote>\n<p>提示：</p>\n<ul>\n<li>S 的长度不超过12。</li>\n<li>S 仅由数字和字母组成。</li>\n</ul>\n<p>友情链接：<a href=\"https://leetcode-cn.com/problems/letter-case-permutation/\">https://leetcode-cn.com/problems/letter-case-permutation/</a></p>\n<h3 id=\"代码实战Ⅰ\"><a href=\"#代码实战Ⅰ\" class=\"headerlink\" title=\"代码实战Ⅰ\"></a>代码实战Ⅰ</h3><figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br><span class=\"line\">31</span><br><span class=\"line\">32</span><br><span class=\"line\">33</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"class\"><span class=\"keyword\">class</span> <span class=\"title\">Solution</span> </span>&#123;</span><br><span class=\"line\">    StringBuilder path = <span class=\"keyword\">new</span> StringBuilder();</span><br><span class=\"line\">    <span class=\"function\"><span class=\"keyword\">public</span> List&lt;String&gt; <span class=\"title\">letterCasePermutation</span><span class=\"params\">(String s)</span> </span>&#123;</span><br><span class=\"line\">        ArrayList&lt;String&gt; res = <span class=\"keyword\">new</span> ArrayList&lt;&gt;();</span><br><span class=\"line\">        backTracking(s, res, <span class=\"number\">0</span>);</span><br><span class=\"line\">        <span class=\"keyword\">return</span> res;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\"></span><br><span class=\"line\">    <span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">void</span> <span class=\"title\">backTracking</span><span class=\"params\">(String s, ArrayList&lt;String&gt; res, <span class=\"keyword\">int</span> index)</span> </span>&#123;</span><br><span class=\"line\">        <span class=\"keyword\">if</span> (path.length() == s.length()) &#123;</span><br><span class=\"line\">            res.add(<span class=\"keyword\">new</span> String(path.toString()));</span><br><span class=\"line\">            <span class=\"keyword\">return</span>;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\"></span><br><span class=\"line\">        <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> i = index; i &lt; s.length(); i++) &#123;</span><br><span class=\"line\">            <span class=\"keyword\">char</span> ch = s.charAt(i);</span><br><span class=\"line\">            <span class=\"keyword\">if</span> (Character.isDigit(ch)) &#123;</span><br><span class=\"line\">                path.append(ch);</span><br><span class=\"line\">                backTracking(s, res, i + <span class=\"number\">1</span>);</span><br><span class=\"line\">                path.deleteCharAt(path.length() - <span class=\"number\">1</span>);</span><br><span class=\"line\">            &#125; <span class=\"keyword\">else</span> &#123;</span><br><span class=\"line\">                path.append(Character.toLowerCase(ch));</span><br><span class=\"line\">                backTracking(s, res, i + <span class=\"number\">1</span>);</span><br><span class=\"line\">                path.deleteCharAt(path.length() - <span class=\"number\">1</span>);</span><br><span class=\"line\"></span><br><span class=\"line\">                path.append(Character.toUpperCase(ch));</span><br><span class=\"line\">                backTracking(s, res, i + <span class=\"number\">1</span>);</span><br><span class=\"line\">                path.deleteCharAt(path.length() - <span class=\"number\">1</span>);</span><br><span class=\"line\">            &#125;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br></pre></td></tr></table></figure>\n\n<p><img src=\"https://p6-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/93356abf8c074eccac4688a4806df115~tplv-k3u1fbpfcp-watermark.image\" class=\"lazyload placeholder\" data-srcset=\"https://p6-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/93356abf8c074eccac4688a4806df115~tplv-k3u1fbpfcp-watermark.image\" srcset=\"https://img2.baidu.com/it/u=2037979560,2772131037&fm=26&fmt=auto&gp=0.jpg\" alt=\"image.png\"></p>\n<h3 id=\"题目实例Ⅱ\"><a href=\"#题目实例Ⅱ\" class=\"headerlink\" title=\"题目实例Ⅱ\"></a>题目实例Ⅱ</h3><p><strong>47. 全排列 II</strong></p>\n<p>给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。</p>\n<p>示例 1：</p>\n<blockquote>\n<p>输入：nums = [1,1,2]</p>\n<p>输出：</p>\n<p>[[1,1,2],</p>\n<p>[1,2,1],</p>\n<p>[2,1,1]]</p>\n</blockquote>\n<p>示例 2：</p>\n<blockquote>\n<p>输入：nums = [1,2,3]</p>\n<p>输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]</p>\n</blockquote>\n<p>提示：</p>\n<ul>\n<li>1 &lt;= nums.length &lt;= 8</li>\n<li>-10 &lt;= nums[i] &lt;= 10</li>\n</ul>\n<p>友情链接：<a href=\"https://leetcode-cn.com/problems/permutations-ii/\">https://leetcode-cn.com/problems/permutations-ii/</a></p>\n<h3 id=\"代码实战Ⅱ\"><a href=\"#代码实战Ⅱ\" class=\"headerlink\" title=\"代码实战Ⅱ\"></a>代码实战Ⅱ</h3><figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"class\"><span class=\"keyword\">class</span> <span class=\"title\">Solution</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">public</span> List&lt;List&lt;Integer&gt;&gt; permuteUnique(<span class=\"keyword\">int</span>[] nums) &#123;</span><br><span class=\"line\">        List&lt;List&lt;Integer&gt;&gt; res = <span class=\"keyword\">new</span> ArrayList&lt;&gt;();</span><br><span class=\"line\">        LinkedList&lt;Integer&gt; path = <span class=\"keyword\">new</span> LinkedList&lt;&gt;();</span><br><span class=\"line\">        <span class=\"keyword\">int</span> depth = <span class=\"number\">0</span>;</span><br><span class=\"line\">        Arrays.sort(nums);</span><br><span class=\"line\">        <span class=\"keyword\">boolean</span>[] used = <span class=\"keyword\">new</span> <span class=\"keyword\">boolean</span>[nums.length];</span><br><span class=\"line\">        backTracking(nums, used, path, depth, res);</span><br><span class=\"line\">        <span class=\"keyword\">return</span> res;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\"></span><br><span class=\"line\">    <span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">backTracking</span><span class=\"params\">(<span class=\"keyword\">int</span>[] nums, <span class=\"keyword\">boolean</span>[] used, LinkedList&lt;Integer&gt; path, <span class=\"keyword\">int</span> depth, List&lt;List&lt;Integer&gt;&gt; res)</span> </span>&#123;</span><br><span class=\"line\">        <span class=\"keyword\">if</span> (nums.length == depth) &#123;</span><br><span class=\"line\">            res.add(<span class=\"keyword\">new</span> ArrayList&lt;&gt;(path));</span><br><span class=\"line\">            <span class=\"keyword\">return</span>;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">        <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> i = <span class=\"number\">0</span>; i &lt; nums.length; i++) &#123;</span><br><span class=\"line\">            <span class=\"keyword\">if</span> (!used[i]) &#123;</span><br><span class=\"line\">                <span class=\"keyword\">if</span> (i &gt; <span class=\"number\">0</span> &amp;&amp; nums[i] == nums[i - <span class=\"number\">1</span>] &amp;&amp; !used[i - <span class=\"number\">1</span>]) &#123;</span><br><span class=\"line\">                    <span class=\"keyword\">continue</span>;</span><br><span class=\"line\">                &#125;</span><br><span class=\"line\">                path.add(nums[i]);</span><br><span class=\"line\">                used[i] = <span class=\"keyword\">true</span>;</span><br><span class=\"line\">                backTracking(nums, used, path, depth + <span class=\"number\">1</span>, res);</span><br><span class=\"line\">                used[i] = <span class=\"keyword\">false</span>;</span><br><span class=\"line\">                path.removeLast();</span><br><span class=\"line\">            &#125;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\">&#125;</span><br></pre></td></tr></table></figure>\n\n\n<p><img src=\"https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/31d9faf5dea64c96934295a1ae01029f~tplv-k3u1fbpfcp-watermark.image\" class=\"lazyload placeholder\" data-srcset=\"https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/31d9faf5dea64c96934295a1ae01029f~tplv-k3u1fbpfcp-watermark.image\" srcset=\"https://img2.baidu.com/it/u=2037979560,2772131037&fm=26&fmt=auto&gp=0.jpg\" alt=\"image.png\"></p>\n","site":{"data":{}},"excerpt":"","more":"<h3 id=\"题目实例Ⅰ\"><a href=\"#题目实例Ⅰ\" class=\"headerlink\" title=\"题目实例Ⅰ\"></a>题目实例Ⅰ</h3><p><strong>784. 字母大小写全排列</strong></p>\n<p>给定一个字符串S，通过将字符串S中的每个字母转变大小写，我们可以获得一个新的字符串。返回所有可能得到的字符串集合。</p>\n<p>示例 1：</p>\n<blockquote>\n<p>输入：S = “a1b2”</p>\n<p>输出：[“a1b2”, “a1B2”, “A1b2”, “A1B2”]</p>\n</blockquote>\n<p>示例 2：</p>\n<blockquote>\n<p>输入：S = “3z4”</p>\n<p>输出：[“3z4”, “3Z4”]</p>\n</blockquote>\n<p>示例 3：</p>\n<blockquote>\n<p>输入：S = “12345”</p>\n<p>输出：[“12345”]</p>\n</blockquote>\n<p>提示：</p>\n<ul>\n<li>S 的长度不超过12。</li>\n<li>S 仅由数字和字母组成。</li>\n</ul>\n<p>友情链接：<a href=\"https://leetcode-cn.com/problems/letter-case-permutation/\">https://leetcode-cn.com/problems/letter-case-permutation/</a></p>\n<h3 id=\"代码实战Ⅰ\"><a href=\"#代码实战Ⅰ\" class=\"headerlink\" title=\"代码实战Ⅰ\"></a>代码实战Ⅰ</h3><figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br><span class=\"line\">31</span><br><span class=\"line\">32</span><br><span class=\"line\">33</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"class\"><span class=\"keyword\">class</span> <span class=\"title\">Solution</span> </span>&#123;</span><br><span class=\"line\">    StringBuilder path = <span class=\"keyword\">new</span> StringBuilder();</span><br><span class=\"line\">    <span class=\"function\"><span class=\"keyword\">public</span> List&lt;String&gt; <span class=\"title\">letterCasePermutation</span><span class=\"params\">(String s)</span> </span>&#123;</span><br><span class=\"line\">        ArrayList&lt;String&gt; res = <span class=\"keyword\">new</span> ArrayList&lt;&gt;();</span><br><span class=\"line\">        backTracking(s, res, <span class=\"number\">0</span>);</span><br><span class=\"line\">        <span class=\"keyword\">return</span> res;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\"></span><br><span class=\"line\">    <span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">void</span> <span class=\"title\">backTracking</span><span class=\"params\">(String s, ArrayList&lt;String&gt; res, <span class=\"keyword\">int</span> index)</span> </span>&#123;</span><br><span class=\"line\">        <span class=\"keyword\">if</span> (path.length() == s.length()) &#123;</span><br><span class=\"line\">            res.add(<span class=\"keyword\">new</span> String(path.toString()));</span><br><span class=\"line\">            <span class=\"keyword\">return</span>;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\"></span><br><span class=\"line\">        <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> i = index; i &lt; s.length(); i++) &#123;</span><br><span class=\"line\">            <span class=\"keyword\">char</span> ch = s.charAt(i);</span><br><span class=\"line\">            <span class=\"keyword\">if</span> (Character.isDigit(ch)) &#123;</span><br><span class=\"line\">                path.append(ch);</span><br><span class=\"line\">                backTracking(s, res, i + <span class=\"number\">1</span>);</span><br><span class=\"line\">                path.deleteCharAt(path.length() - <span class=\"number\">1</span>);</span><br><span class=\"line\">            &#125; <span class=\"keyword\">else</span> &#123;</span><br><span class=\"line\">                path.append(Character.toLowerCase(ch));</span><br><span class=\"line\">                backTracking(s, res, i + <span class=\"number\">1</span>);</span><br><span class=\"line\">                path.deleteCharAt(path.length() - <span class=\"number\">1</span>);</span><br><span class=\"line\"></span><br><span class=\"line\">                path.append(Character.toUpperCase(ch));</span><br><span class=\"line\">                backTracking(s, res, i + <span class=\"number\">1</span>);</span><br><span class=\"line\">                path.deleteCharAt(path.length() - <span class=\"number\">1</span>);</span><br><span class=\"line\">            &#125;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br></pre></td></tr></table></figure>\n\n<p><img src=\"https://p6-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/93356abf8c074eccac4688a4806df115~tplv-k3u1fbpfcp-watermark.image\" alt=\"image.png\"></p>\n<h3 id=\"题目实例Ⅱ\"><a href=\"#题目实例Ⅱ\" class=\"headerlink\" title=\"题目实例Ⅱ\"></a>题目实例Ⅱ</h3><p><strong>47. 全排列 II</strong></p>\n<p>给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。</p>\n<p>示例 1：</p>\n<blockquote>\n<p>输入：nums = [1,1,2]</p>\n<p>输出：</p>\n<p>[[1,1,2],</p>\n<p>[1,2,1],</p>\n<p>[2,1,1]]</p>\n</blockquote>\n<p>示例 2：</p>\n<blockquote>\n<p>输入：nums = [1,2,3]</p>\n<p>输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]</p>\n</blockquote>\n<p>提示：</p>\n<ul>\n<li>1 &lt;= nums.length &lt;= 8</li>\n<li>-10 &lt;= nums[i] &lt;= 10</li>\n</ul>\n<p>友情链接：<a href=\"https://leetcode-cn.com/problems/permutations-ii/\">https://leetcode-cn.com/problems/permutations-ii/</a></p>\n<h3 id=\"代码实战Ⅱ\"><a href=\"#代码实战Ⅱ\" class=\"headerlink\" title=\"代码实战Ⅱ\"></a>代码实战Ⅱ</h3><figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"class\"><span class=\"keyword\">class</span> <span class=\"title\">Solution</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">public</span> List&lt;List&lt;Integer&gt;&gt; permuteUnique(<span class=\"keyword\">int</span>[] nums) &#123;</span><br><span class=\"line\">        List&lt;List&lt;Integer&gt;&gt; res = <span class=\"keyword\">new</span> ArrayList&lt;&gt;();</span><br><span class=\"line\">        LinkedList&lt;Integer&gt; path = <span class=\"keyword\">new</span> LinkedList&lt;&gt;();</span><br><span class=\"line\">        <span class=\"keyword\">int</span> depth = <span class=\"number\">0</span>;</span><br><span class=\"line\">        Arrays.sort(nums);</span><br><span class=\"line\">        <span class=\"keyword\">boolean</span>[] used = <span class=\"keyword\">new</span> <span class=\"keyword\">boolean</span>[nums.length];</span><br><span class=\"line\">        backTracking(nums, used, path, depth, res);</span><br><span class=\"line\">        <span class=\"keyword\">return</span> res;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\"></span><br><span class=\"line\">    <span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">backTracking</span><span class=\"params\">(<span class=\"keyword\">int</span>[] nums, <span class=\"keyword\">boolean</span>[] used, LinkedList&lt;Integer&gt; path, <span class=\"keyword\">int</span> depth, List&lt;List&lt;Integer&gt;&gt; res)</span> </span>&#123;</span><br><span class=\"line\">        <span class=\"keyword\">if</span> (nums.length == depth) &#123;</span><br><span class=\"line\">            res.add(<span class=\"keyword\">new</span> ArrayList&lt;&gt;(path));</span><br><span class=\"line\">            <span class=\"keyword\">return</span>;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">        <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> i = <span class=\"number\">0</span>; i &lt; nums.length; i++) &#123;</span><br><span class=\"line\">            <span class=\"keyword\">if</span> (!used[i]) &#123;</span><br><span class=\"line\">                <span class=\"keyword\">if</span> (i &gt; <span class=\"number\">0</span> &amp;&amp; nums[i] == nums[i - <span class=\"number\">1</span>] &amp;&amp; !used[i - <span class=\"number\">1</span>]) &#123;</span><br><span class=\"line\">                    <span class=\"keyword\">continue</span>;</span><br><span class=\"line\">                &#125;</span><br><span class=\"line\">                path.add(nums[i]);</span><br><span class=\"line\">                used[i] = <span class=\"keyword\">true</span>;</span><br><span class=\"line\">                backTracking(nums, used, path, depth + <span class=\"number\">1</span>, res);</span><br><span class=\"line\">                used[i] = <span class=\"keyword\">false</span>;</span><br><span class=\"line\">                path.removeLast();</span><br><span class=\"line\">            &#125;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\">&#125;</span><br></pre></td></tr></table></figure>\n\n\n<p><img src=\"https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/31d9faf5dea64c96934295a1ae01029f~tplv-k3u1fbpfcp-watermark.image\" alt=\"image.png\"></p>\n"},{"title":"快速排序","date":"2021-06-20T08:49:11.000Z","_content":"\n快速排序算法由 C. A. R. Hoare 在 1960 年提出。它的时间复杂度也是 O(nlogn)，但它在时间复杂度为O(nlogn)级的几种排序算法中，大多数情况下效率更高，所以快速排序的应用非常广泛。再加上快速排序所采用的分治思想非常实用，使得快速排序深受面试官的青睐，所以掌握快速排序的思想尤为重要。\n\n快速排序算法的基本思想是：\n\n- 从数组中取出一个数，称之为基数（pivot）\n- 遍历数组，将比基数大的数字放到它的右边，比基数小的数字放到它的左边。遍历完成后，数组被分成了左右两个区域\n- 将左右两个区域视为两个数组，重复前两个步骤，直到排序完成\n\n事实上，快速排序的每一次遍历，都将基数摆到了最终位置上。第一轮遍历排好 1 个基数，第二轮遍历排好 2 个基数（每个区域一个基数，但如果某个区域为空，则此轮只能排好一个基数），第三轮遍历排好 4 个基数（同理，最差的情况下，只能排好一个基数），以此类推。总遍历次数为 logn～n 次，每轮遍历的时间复杂度为O(n)，所以很容易分析出快速排序的时间复杂度为 O(nlogn)～ O(n^2)平均时间复杂度为O(nlogn)。\n\n*让我们来看一下快速排序的动图吧*\n\n![image.png](/medias/images/QUI.gif)\n\n\n## 快速排序递归框架\n根据我们分析出的思路，先搭出快速排序的架子：\n\n```Java\npublic static void quickSort(int[] arr) {\n  quickSort(arr, 0, arr.length - 1);\n}\npublic static void quickSort(int[] arr, int start, int end) {\n  // 将数组分区，并获得中间值的下标\n  int middle = partition(arr, start, end);\n  // 对左边区域快速排序\n  quickSort(arr, start, middle - 1);\n  // 对右边区域快速排序\n  quickSort(arr, middle + 1, end);\n}\npublic static int partition(int[] arr, int start, int end) {\n  // TODO: 将 arr 从 start 到 end 分区，左边区域比基数小，右边区域比基数大，然后返回中间值的下标\n}\n```\n\n> partition 意为“划分”，我们期望 partition 函数做的事情是：将 arr 从 start 到 end 这一区间的值分成两个区域，左边区域的每个数都比基数小，右边区域的每个数都比基数大，然后返回中间值的下标。\n\n只要有了这个函数，我们就能写出快速排序的递归函数框架。首先调用 partition 函数得到中间值的下标 middle，然后对左边区域执行快速排序，也就是递归调用 quickSort(arr, start, middle - 1)，再对右边区域执行快速排序，也就是递归调用 quickSort(arr, middle + 1, end)。\n\n现在还有一个问题，何时退出这个递归函数呢？\n\n## 退出递归的边界条件\n\n很容易想到，当某个区域只剩下一个数字的时候，自然不需要排序了，此时退出递归函数。实际上还有一种情况，就是某个区域只剩下 0 个数字时，也需要退出递归函数。当 middle 等于 start 或者 end 时，就会出现某个区域剩余数字为 0。\n\n所以我们可以通过这种方式退出递归函数：\n\n```Java\npublic static void quickSort(int[] arr, int start, int end) {\n // 将数组分区，并获得中间值的下标\n  int middle = partition(arr, start, end);\n  // 当左边区域中至少有 2 个数字时，对左边区域快速排序\n  if (start != middle && start != middle - 1) quickSort(arr, start, middle - 1);\n  // 当右边区域中至少有 2 个数字时，对右边区域快速排序\n  if (middle != end && middle != end - 1) quickSort(arr, middle + 1, end);\n}\n```\n\n在递归之前，先判断此区域剩余数字是否为 0 个或者 1 个，当数字至少为 2 个时，才执行这个区域的快速排序。因为我们知道 middle >= start && middle <= end 必然成立，所以判断剩余区域的数字为 0 个或者 1 个也就是指 start 或 end 与 middle 相等或相差 1。\n\n我们来分析一下这四个判断条件：\n\n当 start == middle 时，相当于 quickSort(arr, start, middle - 1) 中的 start == end + 1\n\n当 start == middle - 1 时，相当于 quickSort(arr, start, middle - 1) 中的 start == end\n\n当 middle == end时，相当于 quickSort(arr, middle + 1, end) 中的 start == end + 1\n\n当 middle == end -1时，相当于 quickSort(arr, middle + 1, end) 中的 start == end\n\n综上，我们可以将此边界条件统一移到 quickSort 函数之前：\n\n```Java\nfunc quickSortRecurison(arr []int,start,end int){\n  if start == end || start = end + 1{\n      return \n  }\n  middle = partition(arr,start,end)\n  quickSortRecurison(arr,start,middle-1)\n  qucikSortRecurison(arr,midlle+1,end)\n}\n```\n\n更进一步，由上文所说的 middle >= start && middle <= end 可以推出，除了start == end || start == end + 1这两个条件之外，其他的情况下 start 都小于 end。所以我们可以将这个判断条件再次简写为：\n\n```Java\nfunc quickSortRecurison(arr []int,start,end int){\n  if start >= end{\n      return \n  }\n  middle := partition(arr,start,end)\n  quickSortRecurison(arr,start,middle-1)\n  quickSortRecursion(arr,midlle+1,end)\n}\n```\n\n这样我们就写出了最简洁版的边界条件，我们需要知道，这里的 start >= end 实际上只有两种情况：\n\n- start == end: 表明区域内只有一个数字\n- start == end + 1: 表明区域内一个数字也没有\n不会存在 start 比 end 大 2 或者大 3 之类的。\n\n## 分区算法实现\n快速排序中最重要的便是分区算法，也就是 partition 函数。大多数人都能说出快速排序的整体思路，但实现起来却很难一次写对。主要问题就在于分区时存在的各种边界条件，需要读者亲自动手实践才能加深体会。\n\n上文已经说到，partition 函数需要做的事情就是将 arr 从 start 到 end 分区，左边区域比基数小，右边区域比基数大，然后返回中间值的下标。那么首先我们要做的事情就是选择一个基数，基数我们一般称之为 pivot，意为“轴”。整个数组就像围绕这个轴进行旋转，小于轴的数字旋转到左边，大于轴的数字旋转到右边。\n\n## 基数的选择\n基数的选择没有固定标准，随意选择区间内任何一个数字做基数都可以。通常来讲有三种选择方式：\n\n- 选择第一个元素作为基数\n- 选择最后一个元素作为基数\n- 选择区间内一个随机元素作为基数\n\n选择的基数不同，算法的实现也不同。实际上第三种选择方式的平均时间复杂度是最优的，待会分析时间复杂度时我们会详细说明。\n\n本文通过第一种方式来讲解快速排序：\n\n```Java\nfunc partition(arr []int,start,end int){\n  //取第一个数为基数\n  pivot := arr[start]\n  //从第二个数开始分区\n  left = start + 1\n  //右边界\n  right = end\n}\n```\n\n## 最简单的分区算法\n分区的方式也有很多种，最简单的思路是：从 left 开始，遇到比基数大的数，就交换到数组最后，并将 right 减一，直到 left 和 right 相遇，此时数组就被分成了左右两个区域。再将基数和中间的数交换，返回中间值的下标即可。\n\n按照这个思路，我们敲出了如下代码：\n\n```Java\nfunc swap(arr []int,i,j int){\n  arr[i] = arr[i] ^ arr[j]\n  arr[j] = arr[j] ^ arr[i]\n  arr[i] = arr[i] ^ arr[j]\n}\n\nfunc quickSort(arr []int){\n  quickSortRecursion(arr,0,len(arr)-1)\n}\n\nfunc quickSortRecursion(arr []int,start,end int){\n  if start >= end {\n      return \n  }\n  middle := partition(arr,start,end)\n  quickSortRecursion(arr,start,middle-1)\n  quickSortRecursion(arr,middle+1,end)\n}\n\nfunc partition(arr []int,start,end int)int{\n  pivot := start\n  left = start + 1\n  right = end\n  for left < right{\n      for arr[left] <= pivot && left < right{\n          left ++\n      }\n      //left找到大于基数的数，停下来\n      if left != right{\n          swap(arr,left,right)\n          right--\n      }\n\n  }\n\n  if left == right && arr[right] > pivot{\n      right--\n  }\n  if left != start{\n      swap(arr,left,start)\n  }\n\n  return right\n}\n```\n\n因为我们选择了数组的第一个元素作为基数，并且分完区后，会执行将基数和中间值交换的操作，这就意味着交换后的中间值会被分到左边区域。所以我们需要保证中间值的下标是分区完成后，最后一个比基数小的值，这里我们用 right 来记录这个值。\n\n这段代码有一个细节。首先，在交换 left 和 right 之前，我们判断了 left != right，这是因为如果剩余的数组都比基数小，则 left 会加到 right 才停止，这时不应该发生交换。因为 right 已经指向了最后一个比基数小的值。\n\n但这里的拦截可能会拦截到一种错误情况，如果剩余的数组只有最后一个数比基数大，left 仍然加到 right 停止了，但我们并没有发生交换。所以我们在退出循环后，单独比较了 arr[right] 和 pivot。\n\n实际上，这行单独比较的代码非常巧妙，一共处理了三种情况：\n\n- 一是刚才提到的剩余数组中只有最后一个数比基数大的情况\n- 二是 left 和 right 区间内只有一个值，则初始状态下， left == right，所以 while (left < right) 根本不会进入，所以此时我们单独比较这个值和基数的大小关系\n- 三是剩余数组中每个数都比基数大，此时 right 会持续减小，直到和 left 相等退出循环，此时 left 所在位置的值还没有和 pivot 进行比较，所以我们单独比较 left 所在位置的值和基数的大小关系\n\n## 双指针分区算法\n除了上述的分区算法外，还有一种双指针的分区算法更为常用：从 left 开始，遇到比基数大的数，记录其下标；再从 right 往前遍历，找到第一个比基数小的数，记录其下标；然后交换这两个数。继续遍历，直到 left 和 right 相遇。然后就和刚才的算法一样了，交换基数和中间值，并返回中间值的下标。\n\n代码如下：\n\n```Java\nfunc quickSort(arr []int){\n\n  quickSortRescursion(arr,0,len(arr)-1)\n\n}\n\nfunc quickSortRescursion(arr []int,start,end int){\n  if start >= end {\n      return \n  }\n  //求分区中轴，把数组分区\n  middle := partition(arr,start,end)\n  //向左分区递归，对左分区进行排序\n  quickSortRescursion(arr,start,middle-1)\n  //向右分区递归，对右分区进行排序\n  quickSortRescursion(arr,middle+1,end)\n} \n\nfunc partition(arr []int,start,end int)int{\n  //基数\n  pivot := arr[start]\n  left := start+1\n  right := end\n\n  for left < right{\n      for left < right && arr[left] <= pivot{\n          left++\n      }\n      for left < right && arr[right] >= pivot{\n          right--\n      } \n\n      if left < right{\n          swap(arr,left,right)\n          left++\n          right--\n      }\n  }\n    // 如果 left 和 right 相等，单独比较 arr[right] 和 pivot\n  if left == right && arr[right] > pivot{\n      right--\n  }\n  // 将基数和轴交换\n  if right != start{\n  swap(arr,right,start)\n  }\n  return right\n}\n```\n\n同样地，我们需要在退出循环后，单独比较 left 和 right 的值。\n\n## 时间复杂度 & 空间复杂度\n平均时间复杂度为O(nlogn)，最坏的时间复杂度为O(n^2)，空间复杂度与递归的层数有关，每层递归会生成一些临时变量，所以空间复杂度为 O(logn)~ O(n)，平均空间复杂度为O(logn)\n\n为什么说随机选择剩余数组中的一个元素作为基数的方案平均复杂度是最优的呢？什么情况下快速排序算法的时间复杂度最高，一共有两种情况。\n\n- 数组为正序\n- 数组为逆序\n\n理想中的快速排序在第 k 轮遍历中，可以排好 2^(k-1)个基数。但从图中我们发现，当数组原本为正序或逆序时，我们将第一个数作为基数的话，每轮分区后，都有一个区域是空的，也就是说数组中剩下的数字都被分到了同一个区域！这就导致了每一轮遍历只能排好一个基数。所以总的比较次数为 (n - 1) + (n - 2) + (n - 3) + … + 1 次，由等差数列求和公式可以计算出总的比较次数为 n(n - 1)/2 次，此时快速排序的时间复杂度达到了 O(n^2)级。\n\n## 稳定性\n从代码实现中可以分析出，快速排序是一种不稳定的排序算法，在分区过程中，相同数字的相对顺序可能会被修改。\n\n## 快速排序的优化思路\n- 1.每轮选择基数时，从剩余的数组中随机选择一个数字作为基数。这样每轮都选到最大或最小值的概率就会变得很低了。所以我们才说用这种方式选择基数，其平均时间复杂度是最优的\n- 2.三数取中，待排序序列中low、mid、high三个位置上数据进行排序，取他们中间的那个数据作为枢轴，并用0下标元素存储枢轴。\n","source":"_posts/算法/快速排序.md","raw":"---\ntitle: 快速排序\ndate: 2021-06-20 16:49:11\ntags: [算法,排序]\ncategories: 算法\n---\n\n快速排序算法由 C. A. R. Hoare 在 1960 年提出。它的时间复杂度也是 O(nlogn)，但它在时间复杂度为O(nlogn)级的几种排序算法中，大多数情况下效率更高，所以快速排序的应用非常广泛。再加上快速排序所采用的分治思想非常实用，使得快速排序深受面试官的青睐，所以掌握快速排序的思想尤为重要。\n\n快速排序算法的基本思想是：\n\n- 从数组中取出一个数，称之为基数（pivot）\n- 遍历数组，将比基数大的数字放到它的右边，比基数小的数字放到它的左边。遍历完成后，数组被分成了左右两个区域\n- 将左右两个区域视为两个数组，重复前两个步骤，直到排序完成\n\n事实上，快速排序的每一次遍历，都将基数摆到了最终位置上。第一轮遍历排好 1 个基数，第二轮遍历排好 2 个基数（每个区域一个基数，但如果某个区域为空，则此轮只能排好一个基数），第三轮遍历排好 4 个基数（同理，最差的情况下，只能排好一个基数），以此类推。总遍历次数为 logn～n 次，每轮遍历的时间复杂度为O(n)，所以很容易分析出快速排序的时间复杂度为 O(nlogn)～ O(n^2)平均时间复杂度为O(nlogn)。\n\n*让我们来看一下快速排序的动图吧*\n\n![image.png](/medias/images/QUI.gif)\n\n\n## 快速排序递归框架\n根据我们分析出的思路，先搭出快速排序的架子：\n\n```Java\npublic static void quickSort(int[] arr) {\n  quickSort(arr, 0, arr.length - 1);\n}\npublic static void quickSort(int[] arr, int start, int end) {\n  // 将数组分区，并获得中间值的下标\n  int middle = partition(arr, start, end);\n  // 对左边区域快速排序\n  quickSort(arr, start, middle - 1);\n  // 对右边区域快速排序\n  quickSort(arr, middle + 1, end);\n}\npublic static int partition(int[] arr, int start, int end) {\n  // TODO: 将 arr 从 start 到 end 分区，左边区域比基数小，右边区域比基数大，然后返回中间值的下标\n}\n```\n\n> partition 意为“划分”，我们期望 partition 函数做的事情是：将 arr 从 start 到 end 这一区间的值分成两个区域，左边区域的每个数都比基数小，右边区域的每个数都比基数大，然后返回中间值的下标。\n\n只要有了这个函数，我们就能写出快速排序的递归函数框架。首先调用 partition 函数得到中间值的下标 middle，然后对左边区域执行快速排序，也就是递归调用 quickSort(arr, start, middle - 1)，再对右边区域执行快速排序，也就是递归调用 quickSort(arr, middle + 1, end)。\n\n现在还有一个问题，何时退出这个递归函数呢？\n\n## 退出递归的边界条件\n\n很容易想到，当某个区域只剩下一个数字的时候，自然不需要排序了，此时退出递归函数。实际上还有一种情况，就是某个区域只剩下 0 个数字时，也需要退出递归函数。当 middle 等于 start 或者 end 时，就会出现某个区域剩余数字为 0。\n\n所以我们可以通过这种方式退出递归函数：\n\n```Java\npublic static void quickSort(int[] arr, int start, int end) {\n // 将数组分区，并获得中间值的下标\n  int middle = partition(arr, start, end);\n  // 当左边区域中至少有 2 个数字时，对左边区域快速排序\n  if (start != middle && start != middle - 1) quickSort(arr, start, middle - 1);\n  // 当右边区域中至少有 2 个数字时，对右边区域快速排序\n  if (middle != end && middle != end - 1) quickSort(arr, middle + 1, end);\n}\n```\n\n在递归之前，先判断此区域剩余数字是否为 0 个或者 1 个，当数字至少为 2 个时，才执行这个区域的快速排序。因为我们知道 middle >= start && middle <= end 必然成立，所以判断剩余区域的数字为 0 个或者 1 个也就是指 start 或 end 与 middle 相等或相差 1。\n\n我们来分析一下这四个判断条件：\n\n当 start == middle 时，相当于 quickSort(arr, start, middle - 1) 中的 start == end + 1\n\n当 start == middle - 1 时，相当于 quickSort(arr, start, middle - 1) 中的 start == end\n\n当 middle == end时，相当于 quickSort(arr, middle + 1, end) 中的 start == end + 1\n\n当 middle == end -1时，相当于 quickSort(arr, middle + 1, end) 中的 start == end\n\n综上，我们可以将此边界条件统一移到 quickSort 函数之前：\n\n```Java\nfunc quickSortRecurison(arr []int,start,end int){\n  if start == end || start = end + 1{\n      return \n  }\n  middle = partition(arr,start,end)\n  quickSortRecurison(arr,start,middle-1)\n  qucikSortRecurison(arr,midlle+1,end)\n}\n```\n\n更进一步，由上文所说的 middle >= start && middle <= end 可以推出，除了start == end || start == end + 1这两个条件之外，其他的情况下 start 都小于 end。所以我们可以将这个判断条件再次简写为：\n\n```Java\nfunc quickSortRecurison(arr []int,start,end int){\n  if start >= end{\n      return \n  }\n  middle := partition(arr,start,end)\n  quickSortRecurison(arr,start,middle-1)\n  quickSortRecursion(arr,midlle+1,end)\n}\n```\n\n这样我们就写出了最简洁版的边界条件，我们需要知道，这里的 start >= end 实际上只有两种情况：\n\n- start == end: 表明区域内只有一个数字\n- start == end + 1: 表明区域内一个数字也没有\n不会存在 start 比 end 大 2 或者大 3 之类的。\n\n## 分区算法实现\n快速排序中最重要的便是分区算法，也就是 partition 函数。大多数人都能说出快速排序的整体思路，但实现起来却很难一次写对。主要问题就在于分区时存在的各种边界条件，需要读者亲自动手实践才能加深体会。\n\n上文已经说到，partition 函数需要做的事情就是将 arr 从 start 到 end 分区，左边区域比基数小，右边区域比基数大，然后返回中间值的下标。那么首先我们要做的事情就是选择一个基数，基数我们一般称之为 pivot，意为“轴”。整个数组就像围绕这个轴进行旋转，小于轴的数字旋转到左边，大于轴的数字旋转到右边。\n\n## 基数的选择\n基数的选择没有固定标准，随意选择区间内任何一个数字做基数都可以。通常来讲有三种选择方式：\n\n- 选择第一个元素作为基数\n- 选择最后一个元素作为基数\n- 选择区间内一个随机元素作为基数\n\n选择的基数不同，算法的实现也不同。实际上第三种选择方式的平均时间复杂度是最优的，待会分析时间复杂度时我们会详细说明。\n\n本文通过第一种方式来讲解快速排序：\n\n```Java\nfunc partition(arr []int,start,end int){\n  //取第一个数为基数\n  pivot := arr[start]\n  //从第二个数开始分区\n  left = start + 1\n  //右边界\n  right = end\n}\n```\n\n## 最简单的分区算法\n分区的方式也有很多种，最简单的思路是：从 left 开始，遇到比基数大的数，就交换到数组最后，并将 right 减一，直到 left 和 right 相遇，此时数组就被分成了左右两个区域。再将基数和中间的数交换，返回中间值的下标即可。\n\n按照这个思路，我们敲出了如下代码：\n\n```Java\nfunc swap(arr []int,i,j int){\n  arr[i] = arr[i] ^ arr[j]\n  arr[j] = arr[j] ^ arr[i]\n  arr[i] = arr[i] ^ arr[j]\n}\n\nfunc quickSort(arr []int){\n  quickSortRecursion(arr,0,len(arr)-1)\n}\n\nfunc quickSortRecursion(arr []int,start,end int){\n  if start >= end {\n      return \n  }\n  middle := partition(arr,start,end)\n  quickSortRecursion(arr,start,middle-1)\n  quickSortRecursion(arr,middle+1,end)\n}\n\nfunc partition(arr []int,start,end int)int{\n  pivot := start\n  left = start + 1\n  right = end\n  for left < right{\n      for arr[left] <= pivot && left < right{\n          left ++\n      }\n      //left找到大于基数的数，停下来\n      if left != right{\n          swap(arr,left,right)\n          right--\n      }\n\n  }\n\n  if left == right && arr[right] > pivot{\n      right--\n  }\n  if left != start{\n      swap(arr,left,start)\n  }\n\n  return right\n}\n```\n\n因为我们选择了数组的第一个元素作为基数，并且分完区后，会执行将基数和中间值交换的操作，这就意味着交换后的中间值会被分到左边区域。所以我们需要保证中间值的下标是分区完成后，最后一个比基数小的值，这里我们用 right 来记录这个值。\n\n这段代码有一个细节。首先，在交换 left 和 right 之前，我们判断了 left != right，这是因为如果剩余的数组都比基数小，则 left 会加到 right 才停止，这时不应该发生交换。因为 right 已经指向了最后一个比基数小的值。\n\n但这里的拦截可能会拦截到一种错误情况，如果剩余的数组只有最后一个数比基数大，left 仍然加到 right 停止了，但我们并没有发生交换。所以我们在退出循环后，单独比较了 arr[right] 和 pivot。\n\n实际上，这行单独比较的代码非常巧妙，一共处理了三种情况：\n\n- 一是刚才提到的剩余数组中只有最后一个数比基数大的情况\n- 二是 left 和 right 区间内只有一个值，则初始状态下， left == right，所以 while (left < right) 根本不会进入，所以此时我们单独比较这个值和基数的大小关系\n- 三是剩余数组中每个数都比基数大，此时 right 会持续减小，直到和 left 相等退出循环，此时 left 所在位置的值还没有和 pivot 进行比较，所以我们单独比较 left 所在位置的值和基数的大小关系\n\n## 双指针分区算法\n除了上述的分区算法外，还有一种双指针的分区算法更为常用：从 left 开始，遇到比基数大的数，记录其下标；再从 right 往前遍历，找到第一个比基数小的数，记录其下标；然后交换这两个数。继续遍历，直到 left 和 right 相遇。然后就和刚才的算法一样了，交换基数和中间值，并返回中间值的下标。\n\n代码如下：\n\n```Java\nfunc quickSort(arr []int){\n\n  quickSortRescursion(arr,0,len(arr)-1)\n\n}\n\nfunc quickSortRescursion(arr []int,start,end int){\n  if start >= end {\n      return \n  }\n  //求分区中轴，把数组分区\n  middle := partition(arr,start,end)\n  //向左分区递归，对左分区进行排序\n  quickSortRescursion(arr,start,middle-1)\n  //向右分区递归，对右分区进行排序\n  quickSortRescursion(arr,middle+1,end)\n} \n\nfunc partition(arr []int,start,end int)int{\n  //基数\n  pivot := arr[start]\n  left := start+1\n  right := end\n\n  for left < right{\n      for left < right && arr[left] <= pivot{\n          left++\n      }\n      for left < right && arr[right] >= pivot{\n          right--\n      } \n\n      if left < right{\n          swap(arr,left,right)\n          left++\n          right--\n      }\n  }\n    // 如果 left 和 right 相等，单独比较 arr[right] 和 pivot\n  if left == right && arr[right] > pivot{\n      right--\n  }\n  // 将基数和轴交换\n  if right != start{\n  swap(arr,right,start)\n  }\n  return right\n}\n```\n\n同样地，我们需要在退出循环后，单独比较 left 和 right 的值。\n\n## 时间复杂度 & 空间复杂度\n平均时间复杂度为O(nlogn)，最坏的时间复杂度为O(n^2)，空间复杂度与递归的层数有关，每层递归会生成一些临时变量，所以空间复杂度为 O(logn)~ O(n)，平均空间复杂度为O(logn)\n\n为什么说随机选择剩余数组中的一个元素作为基数的方案平均复杂度是最优的呢？什么情况下快速排序算法的时间复杂度最高，一共有两种情况。\n\n- 数组为正序\n- 数组为逆序\n\n理想中的快速排序在第 k 轮遍历中，可以排好 2^(k-1)个基数。但从图中我们发现，当数组原本为正序或逆序时，我们将第一个数作为基数的话，每轮分区后，都有一个区域是空的，也就是说数组中剩下的数字都被分到了同一个区域！这就导致了每一轮遍历只能排好一个基数。所以总的比较次数为 (n - 1) + (n - 2) + (n - 3) + … + 1 次，由等差数列求和公式可以计算出总的比较次数为 n(n - 1)/2 次，此时快速排序的时间复杂度达到了 O(n^2)级。\n\n## 稳定性\n从代码实现中可以分析出，快速排序是一种不稳定的排序算法，在分区过程中，相同数字的相对顺序可能会被修改。\n\n## 快速排序的优化思路\n- 1.每轮选择基数时，从剩余的数组中随机选择一个数字作为基数。这样每轮都选到最大或最小值的概率就会变得很低了。所以我们才说用这种方式选择基数，其平均时间复杂度是最优的\n- 2.三数取中，待排序序列中low、mid、high三个位置上数据进行排序，取他们中间的那个数据作为枢轴，并用0下标元素存储枢轴。\n","slug":"算法/快速排序","published":1,"updated":"2022-01-28T13:15:02.940Z","comments":1,"layout":"post","photos":[],"link":"","_id":"ckyzjvxny000nsdwog40geqce","content":"<p>快速排序算法由 C. A. R. Hoare 在 1960 年提出。它的时间复杂度也是 O(nlogn)，但它在时间复杂度为O(nlogn)级的几种排序算法中，大多数情况下效率更高，所以快速排序的应用非常广泛。再加上快速排序所采用的分治思想非常实用，使得快速排序深受面试官的青睐，所以掌握快速排序的思想尤为重要。</p>\n<p>快速排序算法的基本思想是：</p>\n<ul>\n<li>从数组中取出一个数，称之为基数（pivot）</li>\n<li>遍历数组，将比基数大的数字放到它的右边，比基数小的数字放到它的左边。遍历完成后，数组被分成了左右两个区域</li>\n<li>将左右两个区域视为两个数组，重复前两个步骤，直到排序完成</li>\n</ul>\n<p>事实上，快速排序的每一次遍历，都将基数摆到了最终位置上。第一轮遍历排好 1 个基数，第二轮遍历排好 2 个基数（每个区域一个基数，但如果某个区域为空，则此轮只能排好一个基数），第三轮遍历排好 4 个基数（同理，最差的情况下，只能排好一个基数），以此类推。总遍历次数为 logn～n 次，每轮遍历的时间复杂度为O(n)，所以很容易分析出快速排序的时间复杂度为 O(nlogn)～ O(n^2)平均时间复杂度为O(nlogn)。</p>\n<p><em>让我们来看一下快速排序的动图吧</em></p>\n<p><img src=\"/medias/images/QUI.gif\" class=\"lazyload placeholder\" data-srcset=\"/medias/images/QUI.gif\" srcset=\"https://img2.baidu.com/it/u=2037979560,2772131037&fm=26&fmt=auto&gp=0.jpg\" alt=\"image.png\"></p>\n<h2 id=\"快速排序递归框架\"><a href=\"#快速排序递归框架\" class=\"headerlink\" title=\"快速排序递归框架\"></a>快速排序递归框架</h2><p>根据我们分析出的思路，先搭出快速排序的架子：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">quickSort</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr)</span> </span>&#123;</span><br><span class=\"line\">  quickSort(arr, <span class=\"number\">0</span>, arr.length - <span class=\"number\">1</span>);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">quickSort</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr, <span class=\"keyword\">int</span> start, <span class=\"keyword\">int</span> end)</span> </span>&#123;</span><br><span class=\"line\">  <span class=\"comment\">// 将数组分区，并获得中间值的下标</span></span><br><span class=\"line\">  <span class=\"keyword\">int</span> middle = partition(arr, start, end);</span><br><span class=\"line\">  <span class=\"comment\">// 对左边区域快速排序</span></span><br><span class=\"line\">  quickSort(arr, start, middle - <span class=\"number\">1</span>);</span><br><span class=\"line\">  <span class=\"comment\">// 对右边区域快速排序</span></span><br><span class=\"line\">  quickSort(arr, middle + <span class=\"number\">1</span>, end);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">int</span> <span class=\"title\">partition</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr, <span class=\"keyword\">int</span> start, <span class=\"keyword\">int</span> end)</span> </span>&#123;</span><br><span class=\"line\">  <span class=\"comment\">// <span class=\"doctag\">TODO:</span> 将 arr 从 start 到 end 分区，左边区域比基数小，右边区域比基数大，然后返回中间值的下标</span></span><br><span class=\"line\">&#125;</span><br></pre></td></tr></table></figure>\n\n<blockquote>\n<p>partition 意为“划分”，我们期望 partition 函数做的事情是：将 arr 从 start 到 end 这一区间的值分成两个区域，左边区域的每个数都比基数小，右边区域的每个数都比基数大，然后返回中间值的下标。</p>\n</blockquote>\n<p>只要有了这个函数，我们就能写出快速排序的递归函数框架。首先调用 partition 函数得到中间值的下标 middle，然后对左边区域执行快速排序，也就是递归调用 quickSort(arr, start, middle - 1)，再对右边区域执行快速排序，也就是递归调用 quickSort(arr, middle + 1, end)。</p>\n<p>现在还有一个问题，何时退出这个递归函数呢？</p>\n<h2 id=\"退出递归的边界条件\"><a href=\"#退出递归的边界条件\" class=\"headerlink\" title=\"退出递归的边界条件\"></a>退出递归的边界条件</h2><p>很容易想到，当某个区域只剩下一个数字的时候，自然不需要排序了，此时退出递归函数。实际上还有一种情况，就是某个区域只剩下 0 个数字时，也需要退出递归函数。当 middle 等于 start 或者 end 时，就会出现某个区域剩余数字为 0。</p>\n<p>所以我们可以通过这种方式退出递归函数：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">quickSort</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr, <span class=\"keyword\">int</span> start, <span class=\"keyword\">int</span> end)</span> </span>&#123;</span><br><span class=\"line\"> <span class=\"comment\">// 将数组分区，并获得中间值的下标</span></span><br><span class=\"line\">  <span class=\"keyword\">int</span> middle = partition(arr, start, end);</span><br><span class=\"line\">  <span class=\"comment\">// 当左边区域中至少有 2 个数字时，对左边区域快速排序</span></span><br><span class=\"line\">  <span class=\"keyword\">if</span> (start != middle &amp;&amp; start != middle - <span class=\"number\">1</span>) quickSort(arr, start, middle - <span class=\"number\">1</span>);</span><br><span class=\"line\">  <span class=\"comment\">// 当右边区域中至少有 2 个数字时，对右边区域快速排序</span></span><br><span class=\"line\">  <span class=\"keyword\">if</span> (middle != end &amp;&amp; middle != end - <span class=\"number\">1</span>) quickSort(arr, middle + <span class=\"number\">1</span>, end);</span><br><span class=\"line\">&#125;</span><br></pre></td></tr></table></figure>\n\n<p>在递归之前，先判断此区域剩余数字是否为 0 个或者 1 个，当数字至少为 2 个时，才执行这个区域的快速排序。因为我们知道 middle &gt;= start &amp;&amp; middle &lt;= end 必然成立，所以判断剩余区域的数字为 0 个或者 1 个也就是指 start 或 end 与 middle 相等或相差 1。</p>\n<p>我们来分析一下这四个判断条件：</p>\n<p>当 start == middle 时，相当于 quickSort(arr, start, middle - 1) 中的 start == end + 1</p>\n<p>当 start == middle - 1 时，相当于 quickSort(arr, start, middle - 1) 中的 start == end</p>\n<p>当 middle == end时，相当于 quickSort(arr, middle + 1, end) 中的 start == end + 1</p>\n<p>当 middle == end -1时，相当于 quickSort(arr, middle + 1, end) 中的 start == end</p>\n<p>综上，我们可以将此边界条件统一移到 quickSort 函数之前：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\">func <span class=\"title\">quickSortRecurison</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>,start,end <span class=\"keyword\">int</span>)</span></span>&#123;</span><br><span class=\"line\">  <span class=\"keyword\">if</span> start == end || start = end + <span class=\"number\">1</span>&#123;</span><br><span class=\"line\">      <span class=\"keyword\">return</span> </span><br><span class=\"line\">  &#125;</span><br><span class=\"line\">  middle = partition(arr,start,end)</span><br><span class=\"line\">  quickSortRecurison(arr,start,middle-<span class=\"number\">1</span>)</span><br><span class=\"line\">  qucikSortRecurison(arr,midlle+<span class=\"number\">1</span>,end)</span><br><span class=\"line\">&#125;</span><br></pre></td></tr></table></figure>\n\n<p>更进一步，由上文所说的 middle &gt;= start &amp;&amp; middle &lt;= end 可以推出，除了start == end || start == end + 1这两个条件之外，其他的情况下 start 都小于 end。所以我们可以将这个判断条件再次简写为：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\">func <span class=\"title\">quickSortRecurison</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>,start,end <span class=\"keyword\">int</span>)</span></span>&#123;</span><br><span class=\"line\">  <span class=\"keyword\">if</span> start &gt;= end&#123;</span><br><span class=\"line\">      <span class=\"keyword\">return</span> </span><br><span class=\"line\">  &#125;</span><br><span class=\"line\">  middle := partition(arr,start,end)</span><br><span class=\"line\">  quickSortRecurison(arr,start,middle-<span class=\"number\">1</span>)</span><br><span class=\"line\">  quickSortRecursion(arr,midlle+<span class=\"number\">1</span>,end)</span><br><span class=\"line\">&#125;</span><br></pre></td></tr></table></figure>\n\n<p>这样我们就写出了最简洁版的边界条件，我们需要知道，这里的 start &gt;= end 实际上只有两种情况：</p>\n<ul>\n<li>start == end: 表明区域内只有一个数字</li>\n<li>start == end + 1: 表明区域内一个数字也没有<br>不会存在 start 比 end 大 2 或者大 3 之类的。</li>\n</ul>\n<h2 id=\"分区算法实现\"><a href=\"#分区算法实现\" class=\"headerlink\" title=\"分区算法实现\"></a>分区算法实现</h2><p>快速排序中最重要的便是分区算法，也就是 partition 函数。大多数人都能说出快速排序的整体思路，但实现起来却很难一次写对。主要问题就在于分区时存在的各种边界条件，需要读者亲自动手实践才能加深体会。</p>\n<p>上文已经说到，partition 函数需要做的事情就是将 arr 从 start 到 end 分区，左边区域比基数小，右边区域比基数大，然后返回中间值的下标。那么首先我们要做的事情就是选择一个基数，基数我们一般称之为 pivot，意为“轴”。整个数组就像围绕这个轴进行旋转，小于轴的数字旋转到左边，大于轴的数字旋转到右边。</p>\n<h2 id=\"基数的选择\"><a href=\"#基数的选择\" class=\"headerlink\" title=\"基数的选择\"></a>基数的选择</h2><p>基数的选择没有固定标准，随意选择区间内任何一个数字做基数都可以。通常来讲有三种选择方式：</p>\n<ul>\n<li>选择第一个元素作为基数</li>\n<li>选择最后一个元素作为基数</li>\n<li>选择区间内一个随机元素作为基数</li>\n</ul>\n<p>选择的基数不同，算法的实现也不同。实际上第三种选择方式的平均时间复杂度是最优的，待会分析时间复杂度时我们会详细说明。</p>\n<p>本文通过第一种方式来讲解快速排序：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\">func <span class=\"title\">partition</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>,start,end <span class=\"keyword\">int</span>)</span></span>&#123;</span><br><span class=\"line\">  <span class=\"comment\">//取第一个数为基数</span></span><br><span class=\"line\">  pivot := arr[start]</span><br><span class=\"line\">  <span class=\"comment\">//从第二个数开始分区</span></span><br><span class=\"line\">  left = start + <span class=\"number\">1</span></span><br><span class=\"line\">  <span class=\"comment\">//右边界</span></span><br><span class=\"line\">  right = end</span><br><span class=\"line\">&#125;</span><br></pre></td></tr></table></figure>\n\n<h2 id=\"最简单的分区算法\"><a href=\"#最简单的分区算法\" class=\"headerlink\" title=\"最简单的分区算法\"></a>最简单的分区算法</h2><p>分区的方式也有很多种，最简单的思路是：从 left 开始，遇到比基数大的数，就交换到数组最后，并将 right 减一，直到 left 和 right 相遇，此时数组就被分成了左右两个区域。再将基数和中间的数交换，返回中间值的下标即可。</p>\n<p>按照这个思路，我们敲出了如下代码：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br><span class=\"line\">31</span><br><span class=\"line\">32</span><br><span class=\"line\">33</span><br><span class=\"line\">34</span><br><span class=\"line\">35</span><br><span class=\"line\">36</span><br><span class=\"line\">37</span><br><span class=\"line\">38</span><br><span class=\"line\">39</span><br><span class=\"line\">40</span><br><span class=\"line\">41</span><br><span class=\"line\">42</span><br><span class=\"line\">43</span><br><span class=\"line\">44</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\">func <span class=\"title\">swap</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>,i,j <span class=\"keyword\">int</span>)</span></span>&#123;</span><br><span class=\"line\">  arr[i] = arr[i] ^ arr[j]</span><br><span class=\"line\">  arr[j] = arr[j] ^ arr[i]</span><br><span class=\"line\">  arr[i] = arr[i] ^ arr[j]</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\">func <span class=\"title\">quickSort</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>)</span></span>&#123;</span><br><span class=\"line\">  quickSortRecursion(arr,<span class=\"number\">0</span>,len(arr)-<span class=\"number\">1</span>)</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\">func <span class=\"title\">quickSortRecursion</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>,start,end <span class=\"keyword\">int</span>)</span></span>&#123;</span><br><span class=\"line\">  <span class=\"keyword\">if</span> start &gt;= end &#123;</span><br><span class=\"line\">      <span class=\"keyword\">return</span> </span><br><span class=\"line\">  &#125;</span><br><span class=\"line\">  middle := partition(arr,start,end)</span><br><span class=\"line\">  quickSortRecursion(arr,start,middle-<span class=\"number\">1</span>)</span><br><span class=\"line\">  quickSortRecursion(arr,middle+<span class=\"number\">1</span>,end)</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\">func <span class=\"title\">partition</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>,start,end <span class=\"keyword\">int</span>)</span><span class=\"keyword\">int</span></span>&#123;</span><br><span class=\"line\">  pivot := start</span><br><span class=\"line\">  left = start + <span class=\"number\">1</span></span><br><span class=\"line\">  right = end</span><br><span class=\"line\">  <span class=\"keyword\">for</span> left &lt; right&#123;</span><br><span class=\"line\">      <span class=\"keyword\">for</span> arr[left] &lt;= pivot &amp;&amp; left &lt; right&#123;</span><br><span class=\"line\">          left ++</span><br><span class=\"line\">      &#125;</span><br><span class=\"line\">      <span class=\"comment\">//left找到大于基数的数，停下来</span></span><br><span class=\"line\">      <span class=\"keyword\">if</span> left != right&#123;</span><br><span class=\"line\">          swap(arr,left,right)</span><br><span class=\"line\">          right--</span><br><span class=\"line\">      &#125;</span><br><span class=\"line\"></span><br><span class=\"line\">  &#125;</span><br><span class=\"line\"></span><br><span class=\"line\">  <span class=\"keyword\">if</span> left == right &amp;&amp; arr[right] &gt; pivot&#123;</span><br><span class=\"line\">      right--</span><br><span class=\"line\">  &#125;</span><br><span class=\"line\">  <span class=\"keyword\">if</span> left != start&#123;</span><br><span class=\"line\">      swap(arr,left,start)</span><br><span class=\"line\">  &#125;</span><br><span class=\"line\"></span><br><span class=\"line\">  <span class=\"keyword\">return</span> right</span><br><span class=\"line\">&#125;</span><br></pre></td></tr></table></figure>\n\n<p>因为我们选择了数组的第一个元素作为基数，并且分完区后，会执行将基数和中间值交换的操作，这就意味着交换后的中间值会被分到左边区域。所以我们需要保证中间值的下标是分区完成后，最后一个比基数小的值，这里我们用 right 来记录这个值。</p>\n<p>这段代码有一个细节。首先，在交换 left 和 right 之前，我们判断了 left != right，这是因为如果剩余的数组都比基数小，则 left 会加到 right 才停止，这时不应该发生交换。因为 right 已经指向了最后一个比基数小的值。</p>\n<p>但这里的拦截可能会拦截到一种错误情况，如果剩余的数组只有最后一个数比基数大，left 仍然加到 right 停止了，但我们并没有发生交换。所以我们在退出循环后，单独比较了 arr[right] 和 pivot。</p>\n<p>实际上，这行单独比较的代码非常巧妙，一共处理了三种情况：</p>\n<ul>\n<li>一是刚才提到的剩余数组中只有最后一个数比基数大的情况</li>\n<li>二是 left 和 right 区间内只有一个值，则初始状态下， left == right，所以 while (left &lt; right) 根本不会进入，所以此时我们单独比较这个值和基数的大小关系</li>\n<li>三是剩余数组中每个数都比基数大，此时 right 会持续减小，直到和 left 相等退出循环，此时 left 所在位置的值还没有和 pivot 进行比较，所以我们单独比较 left 所在位置的值和基数的大小关系</li>\n</ul>\n<h2 id=\"双指针分区算法\"><a href=\"#双指针分区算法\" class=\"headerlink\" title=\"双指针分区算法\"></a>双指针分区算法</h2><p>除了上述的分区算法外，还有一种双指针的分区算法更为常用：从 left 开始，遇到比基数大的数，记录其下标；再从 right 往前遍历，找到第一个比基数小的数，记录其下标；然后交换这两个数。继续遍历，直到 left 和 right 相遇。然后就和刚才的算法一样了，交换基数和中间值，并返回中间值的下标。</p>\n<p>代码如下：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br><span class=\"line\">31</span><br><span class=\"line\">32</span><br><span class=\"line\">33</span><br><span class=\"line\">34</span><br><span class=\"line\">35</span><br><span class=\"line\">36</span><br><span class=\"line\">37</span><br><span class=\"line\">38</span><br><span class=\"line\">39</span><br><span class=\"line\">40</span><br><span class=\"line\">41</span><br><span class=\"line\">42</span><br><span class=\"line\">43</span><br><span class=\"line\">44</span><br><span class=\"line\">45</span><br><span class=\"line\">46</span><br><span class=\"line\">47</span><br><span class=\"line\">48</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\">func <span class=\"title\">quickSort</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>)</span></span>&#123;</span><br><span class=\"line\"></span><br><span class=\"line\">  quickSortRescursion(arr,<span class=\"number\">0</span>,len(arr)-<span class=\"number\">1</span>)</span><br><span class=\"line\"></span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\">func <span class=\"title\">quickSortRescursion</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>,start,end <span class=\"keyword\">int</span>)</span></span>&#123;</span><br><span class=\"line\">  <span class=\"keyword\">if</span> start &gt;= end &#123;</span><br><span class=\"line\">      <span class=\"keyword\">return</span> </span><br><span class=\"line\">  &#125;</span><br><span class=\"line\">  <span class=\"comment\">//求分区中轴，把数组分区</span></span><br><span class=\"line\">  middle := partition(arr,start,end)</span><br><span class=\"line\">  <span class=\"comment\">//向左分区递归，对左分区进行排序</span></span><br><span class=\"line\">  quickSortRescursion(arr,start,middle-<span class=\"number\">1</span>)</span><br><span class=\"line\">  <span class=\"comment\">//向右分区递归，对右分区进行排序</span></span><br><span class=\"line\">  quickSortRescursion(arr,middle+<span class=\"number\">1</span>,end)</span><br><span class=\"line\">&#125; </span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\">func <span class=\"title\">partition</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>,start,end <span class=\"keyword\">int</span>)</span><span class=\"keyword\">int</span></span>&#123;</span><br><span class=\"line\">  <span class=\"comment\">//基数</span></span><br><span class=\"line\">  pivot := arr[start]</span><br><span class=\"line\">  left := start+<span class=\"number\">1</span></span><br><span class=\"line\">  right := end</span><br><span class=\"line\"></span><br><span class=\"line\">  <span class=\"keyword\">for</span> left &lt; right&#123;</span><br><span class=\"line\">      <span class=\"keyword\">for</span> left &lt; right &amp;&amp; arr[left] &lt;= pivot&#123;</span><br><span class=\"line\">          left++</span><br><span class=\"line\">      &#125;</span><br><span class=\"line\">      <span class=\"keyword\">for</span> left &lt; right &amp;&amp; arr[right] &gt;= pivot&#123;</span><br><span class=\"line\">          right--</span><br><span class=\"line\">      &#125; </span><br><span class=\"line\"></span><br><span class=\"line\">      <span class=\"keyword\">if</span> left &lt; right&#123;</span><br><span class=\"line\">          swap(arr,left,right)</span><br><span class=\"line\">          left++</span><br><span class=\"line\">          right--</span><br><span class=\"line\">      &#125;</span><br><span class=\"line\">  &#125;</span><br><span class=\"line\">    <span class=\"comment\">// 如果 left 和 right 相等，单独比较 arr[right] 和 pivot</span></span><br><span class=\"line\">  <span class=\"keyword\">if</span> left == right &amp;&amp; arr[right] &gt; pivot&#123;</span><br><span class=\"line\">      right--</span><br><span class=\"line\">  &#125;</span><br><span class=\"line\">  <span class=\"comment\">// 将基数和轴交换</span></span><br><span class=\"line\">  <span class=\"keyword\">if</span> right != start&#123;</span><br><span class=\"line\">  swap(arr,right,start)</span><br><span class=\"line\">  &#125;</span><br><span class=\"line\">  <span class=\"keyword\">return</span> right</span><br><span class=\"line\">&#125;</span><br></pre></td></tr></table></figure>\n\n<p>同样地，我们需要在退出循环后，单独比较 left 和 right 的值。</p>\n<h2 id=\"时间复杂度-amp-空间复杂度\"><a href=\"#时间复杂度-amp-空间复杂度\" class=\"headerlink\" title=\"时间复杂度 &amp; 空间复杂度\"></a>时间复杂度 &amp; 空间复杂度</h2><p>平均时间复杂度为O(nlogn)，最坏的时间复杂度为O(n^2)，空间复杂度与递归的层数有关，每层递归会生成一些临时变量，所以空间复杂度为 O(logn)~ O(n)，平均空间复杂度为O(logn)</p>\n<p>为什么说随机选择剩余数组中的一个元素作为基数的方案平均复杂度是最优的呢？什么情况下快速排序算法的时间复杂度最高，一共有两种情况。</p>\n<ul>\n<li>数组为正序</li>\n<li>数组为逆序</li>\n</ul>\n<p>理想中的快速排序在第 k 轮遍历中，可以排好 2^(k-1)个基数。但从图中我们发现，当数组原本为正序或逆序时，我们将第一个数作为基数的话，每轮分区后，都有一个区域是空的，也就是说数组中剩下的数字都被分到了同一个区域！这就导致了每一轮遍历只能排好一个基数。所以总的比较次数为 (n - 1) + (n - 2) + (n - 3) + … + 1 次，由等差数列求和公式可以计算出总的比较次数为 n(n - 1)/2 次，此时快速排序的时间复杂度达到了 O(n^2)级。</p>\n<h2 id=\"稳定性\"><a href=\"#稳定性\" class=\"headerlink\" title=\"稳定性\"></a>稳定性</h2><p>从代码实现中可以分析出，快速排序是一种不稳定的排序算法，在分区过程中，相同数字的相对顺序可能会被修改。</p>\n<h2 id=\"快速排序的优化思路\"><a href=\"#快速排序的优化思路\" class=\"headerlink\" title=\"快速排序的优化思路\"></a>快速排序的优化思路</h2><ul>\n<li>1.每轮选择基数时，从剩余的数组中随机选择一个数字作为基数。这样每轮都选到最大或最小值的概率就会变得很低了。所以我们才说用这种方式选择基数，其平均时间复杂度是最优的</li>\n<li>2.三数取中，待排序序列中low、mid、high三个位置上数据进行排序，取他们中间的那个数据作为枢轴，并用0下标元素存储枢轴。</li>\n</ul>\n","site":{"data":{}},"excerpt":"","more":"<p>快速排序算法由 C. A. R. Hoare 在 1960 年提出。它的时间复杂度也是 O(nlogn)，但它在时间复杂度为O(nlogn)级的几种排序算法中，大多数情况下效率更高，所以快速排序的应用非常广泛。再加上快速排序所采用的分治思想非常实用，使得快速排序深受面试官的青睐，所以掌握快速排序的思想尤为重要。</p>\n<p>快速排序算法的基本思想是：</p>\n<ul>\n<li>从数组中取出一个数，称之为基数（pivot）</li>\n<li>遍历数组，将比基数大的数字放到它的右边，比基数小的数字放到它的左边。遍历完成后，数组被分成了左右两个区域</li>\n<li>将左右两个区域视为两个数组，重复前两个步骤，直到排序完成</li>\n</ul>\n<p>事实上，快速排序的每一次遍历，都将基数摆到了最终位置上。第一轮遍历排好 1 个基数，第二轮遍历排好 2 个基数（每个区域一个基数，但如果某个区域为空，则此轮只能排好一个基数），第三轮遍历排好 4 个基数（同理，最差的情况下，只能排好一个基数），以此类推。总遍历次数为 logn～n 次，每轮遍历的时间复杂度为O(n)，所以很容易分析出快速排序的时间复杂度为 O(nlogn)～ O(n^2)平均时间复杂度为O(nlogn)。</p>\n<p><em>让我们来看一下快速排序的动图吧</em></p>\n<p><img src=\"/medias/images/QUI.gif\" alt=\"image.png\"></p>\n<h2 id=\"快速排序递归框架\"><a href=\"#快速排序递归框架\" class=\"headerlink\" title=\"快速排序递归框架\"></a>快速排序递归框架</h2><p>根据我们分析出的思路，先搭出快速排序的架子：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">quickSort</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr)</span> </span>&#123;</span><br><span class=\"line\">  quickSort(arr, <span class=\"number\">0</span>, arr.length - <span class=\"number\">1</span>);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">quickSort</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr, <span class=\"keyword\">int</span> start, <span class=\"keyword\">int</span> end)</span> </span>&#123;</span><br><span class=\"line\">  <span class=\"comment\">// 将数组分区，并获得中间值的下标</span></span><br><span class=\"line\">  <span class=\"keyword\">int</span> middle = partition(arr, start, end);</span><br><span class=\"line\">  <span class=\"comment\">// 对左边区域快速排序</span></span><br><span class=\"line\">  quickSort(arr, start, middle - <span class=\"number\">1</span>);</span><br><span class=\"line\">  <span class=\"comment\">// 对右边区域快速排序</span></span><br><span class=\"line\">  quickSort(arr, middle + <span class=\"number\">1</span>, end);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">int</span> <span class=\"title\">partition</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr, <span class=\"keyword\">int</span> start, <span class=\"keyword\">int</span> end)</span> </span>&#123;</span><br><span class=\"line\">  <span class=\"comment\">// <span class=\"doctag\">TODO:</span> 将 arr 从 start 到 end 分区，左边区域比基数小，右边区域比基数大，然后返回中间值的下标</span></span><br><span class=\"line\">&#125;</span><br></pre></td></tr></table></figure>\n\n<blockquote>\n<p>partition 意为“划分”，我们期望 partition 函数做的事情是：将 arr 从 start 到 end 这一区间的值分成两个区域，左边区域的每个数都比基数小，右边区域的每个数都比基数大，然后返回中间值的下标。</p>\n</blockquote>\n<p>只要有了这个函数，我们就能写出快速排序的递归函数框架。首先调用 partition 函数得到中间值的下标 middle，然后对左边区域执行快速排序，也就是递归调用 quickSort(arr, start, middle - 1)，再对右边区域执行快速排序，也就是递归调用 quickSort(arr, middle + 1, end)。</p>\n<p>现在还有一个问题，何时退出这个递归函数呢？</p>\n<h2 id=\"退出递归的边界条件\"><a href=\"#退出递归的边界条件\" class=\"headerlink\" title=\"退出递归的边界条件\"></a>退出递归的边界条件</h2><p>很容易想到，当某个区域只剩下一个数字的时候，自然不需要排序了，此时退出递归函数。实际上还有一种情况，就是某个区域只剩下 0 个数字时，也需要退出递归函数。当 middle 等于 start 或者 end 时，就会出现某个区域剩余数字为 0。</p>\n<p>所以我们可以通过这种方式退出递归函数：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">quickSort</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr, <span class=\"keyword\">int</span> start, <span class=\"keyword\">int</span> end)</span> </span>&#123;</span><br><span class=\"line\"> <span class=\"comment\">// 将数组分区，并获得中间值的下标</span></span><br><span class=\"line\">  <span class=\"keyword\">int</span> middle = partition(arr, start, end);</span><br><span class=\"line\">  <span class=\"comment\">// 当左边区域中至少有 2 个数字时，对左边区域快速排序</span></span><br><span class=\"line\">  <span class=\"keyword\">if</span> (start != middle &amp;&amp; start != middle - <span class=\"number\">1</span>) quickSort(arr, start, middle - <span class=\"number\">1</span>);</span><br><span class=\"line\">  <span class=\"comment\">// 当右边区域中至少有 2 个数字时，对右边区域快速排序</span></span><br><span class=\"line\">  <span class=\"keyword\">if</span> (middle != end &amp;&amp; middle != end - <span class=\"number\">1</span>) quickSort(arr, middle + <span class=\"number\">1</span>, end);</span><br><span class=\"line\">&#125;</span><br></pre></td></tr></table></figure>\n\n<p>在递归之前，先判断此区域剩余数字是否为 0 个或者 1 个，当数字至少为 2 个时，才执行这个区域的快速排序。因为我们知道 middle &gt;= start &amp;&amp; middle &lt;= end 必然成立，所以判断剩余区域的数字为 0 个或者 1 个也就是指 start 或 end 与 middle 相等或相差 1。</p>\n<p>我们来分析一下这四个判断条件：</p>\n<p>当 start == middle 时，相当于 quickSort(arr, start, middle - 1) 中的 start == end + 1</p>\n<p>当 start == middle - 1 时，相当于 quickSort(arr, start, middle - 1) 中的 start == end</p>\n<p>当 middle == end时，相当于 quickSort(arr, middle + 1, end) 中的 start == end + 1</p>\n<p>当 middle == end -1时，相当于 quickSort(arr, middle + 1, end) 中的 start == end</p>\n<p>综上，我们可以将此边界条件统一移到 quickSort 函数之前：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\">func <span class=\"title\">quickSortRecurison</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>,start,end <span class=\"keyword\">int</span>)</span></span>&#123;</span><br><span class=\"line\">  <span class=\"keyword\">if</span> start == end || start = end + <span class=\"number\">1</span>&#123;</span><br><span class=\"line\">      <span class=\"keyword\">return</span> </span><br><span class=\"line\">  &#125;</span><br><span class=\"line\">  middle = partition(arr,start,end)</span><br><span class=\"line\">  quickSortRecurison(arr,start,middle-<span class=\"number\">1</span>)</span><br><span class=\"line\">  qucikSortRecurison(arr,midlle+<span class=\"number\">1</span>,end)</span><br><span class=\"line\">&#125;</span><br></pre></td></tr></table></figure>\n\n<p>更进一步，由上文所说的 middle &gt;= start &amp;&amp; middle &lt;= end 可以推出，除了start == end || start == end + 1这两个条件之外，其他的情况下 start 都小于 end。所以我们可以将这个判断条件再次简写为：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\">func <span class=\"title\">quickSortRecurison</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>,start,end <span class=\"keyword\">int</span>)</span></span>&#123;</span><br><span class=\"line\">  <span class=\"keyword\">if</span> start &gt;= end&#123;</span><br><span class=\"line\">      <span class=\"keyword\">return</span> </span><br><span class=\"line\">  &#125;</span><br><span class=\"line\">  middle := partition(arr,start,end)</span><br><span class=\"line\">  quickSortRecurison(arr,start,middle-<span class=\"number\">1</span>)</span><br><span class=\"line\">  quickSortRecursion(arr,midlle+<span class=\"number\">1</span>,end)</span><br><span class=\"line\">&#125;</span><br></pre></td></tr></table></figure>\n\n<p>这样我们就写出了最简洁版的边界条件，我们需要知道，这里的 start &gt;= end 实际上只有两种情况：</p>\n<ul>\n<li>start == end: 表明区域内只有一个数字</li>\n<li>start == end + 1: 表明区域内一个数字也没有<br>不会存在 start 比 end 大 2 或者大 3 之类的。</li>\n</ul>\n<h2 id=\"分区算法实现\"><a href=\"#分区算法实现\" class=\"headerlink\" title=\"分区算法实现\"></a>分区算法实现</h2><p>快速排序中最重要的便是分区算法，也就是 partition 函数。大多数人都能说出快速排序的整体思路，但实现起来却很难一次写对。主要问题就在于分区时存在的各种边界条件，需要读者亲自动手实践才能加深体会。</p>\n<p>上文已经说到，partition 函数需要做的事情就是将 arr 从 start 到 end 分区，左边区域比基数小，右边区域比基数大，然后返回中间值的下标。那么首先我们要做的事情就是选择一个基数，基数我们一般称之为 pivot，意为“轴”。整个数组就像围绕这个轴进行旋转，小于轴的数字旋转到左边，大于轴的数字旋转到右边。</p>\n<h2 id=\"基数的选择\"><a href=\"#基数的选择\" class=\"headerlink\" title=\"基数的选择\"></a>基数的选择</h2><p>基数的选择没有固定标准，随意选择区间内任何一个数字做基数都可以。通常来讲有三种选择方式：</p>\n<ul>\n<li>选择第一个元素作为基数</li>\n<li>选择最后一个元素作为基数</li>\n<li>选择区间内一个随机元素作为基数</li>\n</ul>\n<p>选择的基数不同，算法的实现也不同。实际上第三种选择方式的平均时间复杂度是最优的，待会分析时间复杂度时我们会详细说明。</p>\n<p>本文通过第一种方式来讲解快速排序：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\">func <span class=\"title\">partition</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>,start,end <span class=\"keyword\">int</span>)</span></span>&#123;</span><br><span class=\"line\">  <span class=\"comment\">//取第一个数为基数</span></span><br><span class=\"line\">  pivot := arr[start]</span><br><span class=\"line\">  <span class=\"comment\">//从第二个数开始分区</span></span><br><span class=\"line\">  left = start + <span class=\"number\">1</span></span><br><span class=\"line\">  <span class=\"comment\">//右边界</span></span><br><span class=\"line\">  right = end</span><br><span class=\"line\">&#125;</span><br></pre></td></tr></table></figure>\n\n<h2 id=\"最简单的分区算法\"><a href=\"#最简单的分区算法\" class=\"headerlink\" title=\"最简单的分区算法\"></a>最简单的分区算法</h2><p>分区的方式也有很多种，最简单的思路是：从 left 开始，遇到比基数大的数，就交换到数组最后，并将 right 减一，直到 left 和 right 相遇，此时数组就被分成了左右两个区域。再将基数和中间的数交换，返回中间值的下标即可。</p>\n<p>按照这个思路，我们敲出了如下代码：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br><span class=\"line\">31</span><br><span class=\"line\">32</span><br><span class=\"line\">33</span><br><span class=\"line\">34</span><br><span class=\"line\">35</span><br><span class=\"line\">36</span><br><span class=\"line\">37</span><br><span class=\"line\">38</span><br><span class=\"line\">39</span><br><span class=\"line\">40</span><br><span class=\"line\">41</span><br><span class=\"line\">42</span><br><span class=\"line\">43</span><br><span class=\"line\">44</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\">func <span class=\"title\">swap</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>,i,j <span class=\"keyword\">int</span>)</span></span>&#123;</span><br><span class=\"line\">  arr[i] = arr[i] ^ arr[j]</span><br><span class=\"line\">  arr[j] = arr[j] ^ arr[i]</span><br><span class=\"line\">  arr[i] = arr[i] ^ arr[j]</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\">func <span class=\"title\">quickSort</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>)</span></span>&#123;</span><br><span class=\"line\">  quickSortRecursion(arr,<span class=\"number\">0</span>,len(arr)-<span class=\"number\">1</span>)</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\">func <span class=\"title\">quickSortRecursion</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>,start,end <span class=\"keyword\">int</span>)</span></span>&#123;</span><br><span class=\"line\">  <span class=\"keyword\">if</span> start &gt;= end &#123;</span><br><span class=\"line\">      <span class=\"keyword\">return</span> </span><br><span class=\"line\">  &#125;</span><br><span class=\"line\">  middle := partition(arr,start,end)</span><br><span class=\"line\">  quickSortRecursion(arr,start,middle-<span class=\"number\">1</span>)</span><br><span class=\"line\">  quickSortRecursion(arr,middle+<span class=\"number\">1</span>,end)</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\">func <span class=\"title\">partition</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>,start,end <span class=\"keyword\">int</span>)</span><span class=\"keyword\">int</span></span>&#123;</span><br><span class=\"line\">  pivot := start</span><br><span class=\"line\">  left = start + <span class=\"number\">1</span></span><br><span class=\"line\">  right = end</span><br><span class=\"line\">  <span class=\"keyword\">for</span> left &lt; right&#123;</span><br><span class=\"line\">      <span class=\"keyword\">for</span> arr[left] &lt;= pivot &amp;&amp; left &lt; right&#123;</span><br><span class=\"line\">          left ++</span><br><span class=\"line\">      &#125;</span><br><span class=\"line\">      <span class=\"comment\">//left找到大于基数的数，停下来</span></span><br><span class=\"line\">      <span class=\"keyword\">if</span> left != right&#123;</span><br><span class=\"line\">          swap(arr,left,right)</span><br><span class=\"line\">          right--</span><br><span class=\"line\">      &#125;</span><br><span class=\"line\"></span><br><span class=\"line\">  &#125;</span><br><span class=\"line\"></span><br><span class=\"line\">  <span class=\"keyword\">if</span> left == right &amp;&amp; arr[right] &gt; pivot&#123;</span><br><span class=\"line\">      right--</span><br><span class=\"line\">  &#125;</span><br><span class=\"line\">  <span class=\"keyword\">if</span> left != start&#123;</span><br><span class=\"line\">      swap(arr,left,start)</span><br><span class=\"line\">  &#125;</span><br><span class=\"line\"></span><br><span class=\"line\">  <span class=\"keyword\">return</span> right</span><br><span class=\"line\">&#125;</span><br></pre></td></tr></table></figure>\n\n<p>因为我们选择了数组的第一个元素作为基数，并且分完区后，会执行将基数和中间值交换的操作，这就意味着交换后的中间值会被分到左边区域。所以我们需要保证中间值的下标是分区完成后，最后一个比基数小的值，这里我们用 right 来记录这个值。</p>\n<p>这段代码有一个细节。首先，在交换 left 和 right 之前，我们判断了 left != right，这是因为如果剩余的数组都比基数小，则 left 会加到 right 才停止，这时不应该发生交换。因为 right 已经指向了最后一个比基数小的值。</p>\n<p>但这里的拦截可能会拦截到一种错误情况，如果剩余的数组只有最后一个数比基数大，left 仍然加到 right 停止了，但我们并没有发生交换。所以我们在退出循环后，单独比较了 arr[right] 和 pivot。</p>\n<p>实际上，这行单独比较的代码非常巧妙，一共处理了三种情况：</p>\n<ul>\n<li>一是刚才提到的剩余数组中只有最后一个数比基数大的情况</li>\n<li>二是 left 和 right 区间内只有一个值，则初始状态下， left == right，所以 while (left &lt; right) 根本不会进入，所以此时我们单独比较这个值和基数的大小关系</li>\n<li>三是剩余数组中每个数都比基数大，此时 right 会持续减小，直到和 left 相等退出循环，此时 left 所在位置的值还没有和 pivot 进行比较，所以我们单独比较 left 所在位置的值和基数的大小关系</li>\n</ul>\n<h2 id=\"双指针分区算法\"><a href=\"#双指针分区算法\" class=\"headerlink\" title=\"双指针分区算法\"></a>双指针分区算法</h2><p>除了上述的分区算法外，还有一种双指针的分区算法更为常用：从 left 开始，遇到比基数大的数，记录其下标；再从 right 往前遍历，找到第一个比基数小的数，记录其下标；然后交换这两个数。继续遍历，直到 left 和 right 相遇。然后就和刚才的算法一样了，交换基数和中间值，并返回中间值的下标。</p>\n<p>代码如下：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br><span class=\"line\">31</span><br><span class=\"line\">32</span><br><span class=\"line\">33</span><br><span class=\"line\">34</span><br><span class=\"line\">35</span><br><span class=\"line\">36</span><br><span class=\"line\">37</span><br><span class=\"line\">38</span><br><span class=\"line\">39</span><br><span class=\"line\">40</span><br><span class=\"line\">41</span><br><span class=\"line\">42</span><br><span class=\"line\">43</span><br><span class=\"line\">44</span><br><span class=\"line\">45</span><br><span class=\"line\">46</span><br><span class=\"line\">47</span><br><span class=\"line\">48</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\">func <span class=\"title\">quickSort</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>)</span></span>&#123;</span><br><span class=\"line\"></span><br><span class=\"line\">  quickSortRescursion(arr,<span class=\"number\">0</span>,len(arr)-<span class=\"number\">1</span>)</span><br><span class=\"line\"></span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\">func <span class=\"title\">quickSortRescursion</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>,start,end <span class=\"keyword\">int</span>)</span></span>&#123;</span><br><span class=\"line\">  <span class=\"keyword\">if</span> start &gt;= end &#123;</span><br><span class=\"line\">      <span class=\"keyword\">return</span> </span><br><span class=\"line\">  &#125;</span><br><span class=\"line\">  <span class=\"comment\">//求分区中轴，把数组分区</span></span><br><span class=\"line\">  middle := partition(arr,start,end)</span><br><span class=\"line\">  <span class=\"comment\">//向左分区递归，对左分区进行排序</span></span><br><span class=\"line\">  quickSortRescursion(arr,start,middle-<span class=\"number\">1</span>)</span><br><span class=\"line\">  <span class=\"comment\">//向右分区递归，对右分区进行排序</span></span><br><span class=\"line\">  quickSortRescursion(arr,middle+<span class=\"number\">1</span>,end)</span><br><span class=\"line\">&#125; </span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\">func <span class=\"title\">partition</span><span class=\"params\">(arr []<span class=\"keyword\">int</span>,start,end <span class=\"keyword\">int</span>)</span><span class=\"keyword\">int</span></span>&#123;</span><br><span class=\"line\">  <span class=\"comment\">//基数</span></span><br><span class=\"line\">  pivot := arr[start]</span><br><span class=\"line\">  left := start+<span class=\"number\">1</span></span><br><span class=\"line\">  right := end</span><br><span class=\"line\"></span><br><span class=\"line\">  <span class=\"keyword\">for</span> left &lt; right&#123;</span><br><span class=\"line\">      <span class=\"keyword\">for</span> left &lt; right &amp;&amp; arr[left] &lt;= pivot&#123;</span><br><span class=\"line\">          left++</span><br><span class=\"line\">      &#125;</span><br><span class=\"line\">      <span class=\"keyword\">for</span> left &lt; right &amp;&amp; arr[right] &gt;= pivot&#123;</span><br><span class=\"line\">          right--</span><br><span class=\"line\">      &#125; </span><br><span class=\"line\"></span><br><span class=\"line\">      <span class=\"keyword\">if</span> left &lt; right&#123;</span><br><span class=\"line\">          swap(arr,left,right)</span><br><span class=\"line\">          left++</span><br><span class=\"line\">          right--</span><br><span class=\"line\">      &#125;</span><br><span class=\"line\">  &#125;</span><br><span class=\"line\">    <span class=\"comment\">// 如果 left 和 right 相等，单独比较 arr[right] 和 pivot</span></span><br><span class=\"line\">  <span class=\"keyword\">if</span> left == right &amp;&amp; arr[right] &gt; pivot&#123;</span><br><span class=\"line\">      right--</span><br><span class=\"line\">  &#125;</span><br><span class=\"line\">  <span class=\"comment\">// 将基数和轴交换</span></span><br><span class=\"line\">  <span class=\"keyword\">if</span> right != start&#123;</span><br><span class=\"line\">  swap(arr,right,start)</span><br><span class=\"line\">  &#125;</span><br><span class=\"line\">  <span class=\"keyword\">return</span> right</span><br><span class=\"line\">&#125;</span><br></pre></td></tr></table></figure>\n\n<p>同样地，我们需要在退出循环后，单独比较 left 和 right 的值。</p>\n<h2 id=\"时间复杂度-amp-空间复杂度\"><a href=\"#时间复杂度-amp-空间复杂度\" class=\"headerlink\" title=\"时间复杂度 &amp; 空间复杂度\"></a>时间复杂度 &amp; 空间复杂度</h2><p>平均时间复杂度为O(nlogn)，最坏的时间复杂度为O(n^2)，空间复杂度与递归的层数有关，每层递归会生成一些临时变量，所以空间复杂度为 O(logn)~ O(n)，平均空间复杂度为O(logn)</p>\n<p>为什么说随机选择剩余数组中的一个元素作为基数的方案平均复杂度是最优的呢？什么情况下快速排序算法的时间复杂度最高，一共有两种情况。</p>\n<ul>\n<li>数组为正序</li>\n<li>数组为逆序</li>\n</ul>\n<p>理想中的快速排序在第 k 轮遍历中，可以排好 2^(k-1)个基数。但从图中我们发现，当数组原本为正序或逆序时，我们将第一个数作为基数的话，每轮分区后，都有一个区域是空的，也就是说数组中剩下的数字都被分到了同一个区域！这就导致了每一轮遍历只能排好一个基数。所以总的比较次数为 (n - 1) + (n - 2) + (n - 3) + … + 1 次，由等差数列求和公式可以计算出总的比较次数为 n(n - 1)/2 次，此时快速排序的时间复杂度达到了 O(n^2)级。</p>\n<h2 id=\"稳定性\"><a href=\"#稳定性\" class=\"headerlink\" title=\"稳定性\"></a>稳定性</h2><p>从代码实现中可以分析出，快速排序是一种不稳定的排序算法，在分区过程中，相同数字的相对顺序可能会被修改。</p>\n<h2 id=\"快速排序的优化思路\"><a href=\"#快速排序的优化思路\" class=\"headerlink\" title=\"快速排序的优化思路\"></a>快速排序的优化思路</h2><ul>\n<li>1.每轮选择基数时，从剩余的数组中随机选择一个数字作为基数。这样每轮都选到最大或最小值的概率就会变得很低了。所以我们才说用这种方式选择基数，其平均时间复杂度是最优的</li>\n<li>2.三数取中，待排序序列中low、mid、high三个位置上数据进行排序，取他们中间的那个数据作为枢轴，并用0下标元素存储枢轴。</li>\n</ul>\n"},{"title":"有趣的位运算","date":"2021-07-23T00:50:12.000Z","_content":"\n## 两数交换 —— 位运算实现\n注意：两个数一定不能指向同一内存空间，不然结果都会变成0！\n\n``` java\nint a,b;\na = a^b;\nb = a^b;\na = a^b;\n```\n\n二进制异或运算 0^1 , 0^0 , 1^1 。相同为 0 ，不同为 1 。\n\n运用到具体两个数字上，就是相同两数异或会为 0 ， 0 再异或任何一个非零的数，就是这个数本身。\n\n异或有交换律和结合律。\n\n## 运用实战\n### 问题1\n**给一个数组 arr[] ，有一种数出现了奇数次，其它数都出现了偶数次，让你把那出现奇数次的数找出来**\n\n```\nint[] arr=new int[]{2,2,3,3,4,4,5,5,5};\nint res=0;\nfor (int cur : arr) {\n    res ^=cur;\n}\nreturn res;\n```\n\n**给一个数组 arr[] ，有两种数出现了奇数次，其它数都出现了偶数次，让你把那出现奇数次的两种数找出来**\n\n```java\n\n  int[] arr = new int[]{2, 2, 3, 3, 4, 4, 5, 5, 5, 6, 6, 6};\n  int eor = 0;\n  for (int cur : arr) {\n      eor ^= cur;\n  }\n  //eor=a^b\n  //eor!=0\n  //eor必然有一个位置为1\n  int rightOne = eor & (~eor + 1);//提取出最右的1\n  int onlyOne = 0;\n  for (int cur : arr) {\n      if ((rightOne & cur) == 0) { //与运算。最右的 1 只有与上 1 才能等于 1 。\n          onlyOne ^= cur;\n      }\n  }//把其中一个数提取出来了 onlyOne = a || b\n  System.out.println(onlyOne + \" \" + (eor ^ onlyOne));\n```\n\n- 与运算。只有两个位都等于 1 时，结果才为 1\n- 或运算。只要有 1 个位为 1 ，结果就为 1\n- 异或运算。如果两个位为“异”（值不同），结果就为 1 。\n\n## 时间复杂度\n算法在**最坏情况**下运行所需时间。\n","source":"_posts/算法/有趣的位运算.md","raw":"---\ntitle: 有趣的位运算\ndate: 2021-07-23 08:50:12\ntags: [算法,学习]\ncategories: 算法\n---\n\n## 两数交换 —— 位运算实现\n注意：两个数一定不能指向同一内存空间，不然结果都会变成0！\n\n``` java\nint a,b;\na = a^b;\nb = a^b;\na = a^b;\n```\n\n二进制异或运算 0^1 , 0^0 , 1^1 。相同为 0 ，不同为 1 。\n\n运用到具体两个数字上，就是相同两数异或会为 0 ， 0 再异或任何一个非零的数，就是这个数本身。\n\n异或有交换律和结合律。\n\n## 运用实战\n### 问题1\n**给一个数组 arr[] ，有一种数出现了奇数次，其它数都出现了偶数次，让你把那出现奇数次的数找出来**\n\n```\nint[] arr=new int[]{2,2,3,3,4,4,5,5,5};\nint res=0;\nfor (int cur : arr) {\n    res ^=cur;\n}\nreturn res;\n```\n\n**给一个数组 arr[] ，有两种数出现了奇数次，其它数都出现了偶数次，让你把那出现奇数次的两种数找出来**\n\n```java\n\n  int[] arr = new int[]{2, 2, 3, 3, 4, 4, 5, 5, 5, 6, 6, 6};\n  int eor = 0;\n  for (int cur : arr) {\n      eor ^= cur;\n  }\n  //eor=a^b\n  //eor!=0\n  //eor必然有一个位置为1\n  int rightOne = eor & (~eor + 1);//提取出最右的1\n  int onlyOne = 0;\n  for (int cur : arr) {\n      if ((rightOne & cur) == 0) { //与运算。最右的 1 只有与上 1 才能等于 1 。\n          onlyOne ^= cur;\n      }\n  }//把其中一个数提取出来了 onlyOne = a || b\n  System.out.println(onlyOne + \" \" + (eor ^ onlyOne));\n```\n\n- 与运算。只有两个位都等于 1 时，结果才为 1\n- 或运算。只要有 1 个位为 1 ，结果就为 1\n- 异或运算。如果两个位为“异”（值不同），结果就为 1 。\n\n## 时间复杂度\n算法在**最坏情况**下运行所需时间。\n","slug":"算法/有趣的位运算","published":1,"updated":"2022-01-28T13:15:02.940Z","comments":1,"layout":"post","photos":[],"link":"","_id":"ckyzjvxnz000rsdwo4qv0b2mk","content":"<h2 id=\"两数交换-——-位运算实现\"><a href=\"#两数交换-——-位运算实现\" class=\"headerlink\" title=\"两数交换 —— 位运算实现\"></a>两数交换 —— 位运算实现</h2><p>注意：两个数一定不能指向同一内存空间，不然结果都会变成0！</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"keyword\">int</span> a,b;</span><br><span class=\"line\">a = a^b;</span><br><span class=\"line\">b = a^b;</span><br><span class=\"line\">a = a^b;</span><br></pre></td></tr></table></figure>\n\n<p>二进制异或运算 0^1 , 0^0 , 1^1 。相同为 0 ，不同为 1 。</p>\n<p>运用到具体两个数字上，就是相同两数异或会为 0 ， 0 再异或任何一个非零的数，就是这个数本身。</p>\n<p>异或有交换律和结合律。</p>\n<h2 id=\"运用实战\"><a href=\"#运用实战\" class=\"headerlink\" title=\"运用实战\"></a>运用实战</h2><h3 id=\"问题1\"><a href=\"#问题1\" class=\"headerlink\" title=\"问题1\"></a>问题1</h3><p><strong>给一个数组 arr[] ，有一种数出现了奇数次，其它数都出现了偶数次，让你把那出现奇数次的数找出来</strong></p>\n<figure class=\"highlight plaintext\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br></pre></td><td class=\"code\"><pre><span class=\"line\">int[] arr=new int[]&#123;2,2,3,3,4,4,5,5,5&#125;;</span><br><span class=\"line\">int res=0;</span><br><span class=\"line\">for (int cur : arr) &#123;</span><br><span class=\"line\">    res ^=cur;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\">return res;</span><br></pre></td></tr></table></figure>\n\n<p><strong>给一个数组 arr[] ，有两种数出现了奇数次，其它数都出现了偶数次，让你把那出现奇数次的两种数找出来</strong></p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"></span><br><span class=\"line\"><span class=\"keyword\">int</span>[] arr = <span class=\"keyword\">new</span> <span class=\"keyword\">int</span>[]&#123;<span class=\"number\">2</span>, <span class=\"number\">2</span>, <span class=\"number\">3</span>, <span class=\"number\">3</span>, <span class=\"number\">4</span>, <span class=\"number\">4</span>, <span class=\"number\">5</span>, <span class=\"number\">5</span>, <span class=\"number\">5</span>, <span class=\"number\">6</span>, <span class=\"number\">6</span>, <span class=\"number\">6</span>&#125;;</span><br><span class=\"line\"><span class=\"keyword\">int</span> eor = <span class=\"number\">0</span>;</span><br><span class=\"line\"><span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> cur : arr) &#123;</span><br><span class=\"line\">    eor ^= cur;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"><span class=\"comment\">//eor=a^b</span></span><br><span class=\"line\"><span class=\"comment\">//eor!=0</span></span><br><span class=\"line\"><span class=\"comment\">//eor必然有一个位置为1</span></span><br><span class=\"line\"><span class=\"keyword\">int</span> rightOne = eor &amp; (~eor + <span class=\"number\">1</span>);<span class=\"comment\">//提取出最右的1</span></span><br><span class=\"line\"><span class=\"keyword\">int</span> onlyOne = <span class=\"number\">0</span>;</span><br><span class=\"line\"><span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> cur : arr) &#123;</span><br><span class=\"line\">    <span class=\"keyword\">if</span> ((rightOne &amp; cur) == <span class=\"number\">0</span>) &#123; <span class=\"comment\">//与运算。最右的 1 只有与上 1 才能等于 1 。</span></span><br><span class=\"line\">        onlyOne ^= cur;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\">&#125;<span class=\"comment\">//把其中一个数提取出来了 onlyOne = a || b</span></span><br><span class=\"line\">System.out.println(onlyOne + <span class=\"string\">&quot; &quot;</span> + (eor ^ onlyOne));</span><br></pre></td></tr></table></figure>\n\n<ul>\n<li>与运算。只有两个位都等于 1 时，结果才为 1</li>\n<li>或运算。只要有 1 个位为 1 ，结果就为 1</li>\n<li>异或运算。如果两个位为“异”（值不同），结果就为 1 。</li>\n</ul>\n<h2 id=\"时间复杂度\"><a href=\"#时间复杂度\" class=\"headerlink\" title=\"时间复杂度\"></a>时间复杂度</h2><p>算法在<strong>最坏情况</strong>下运行所需时间。</p>\n","site":{"data":{}},"excerpt":"","more":"<h2 id=\"两数交换-——-位运算实现\"><a href=\"#两数交换-——-位运算实现\" class=\"headerlink\" title=\"两数交换 —— 位运算实现\"></a>两数交换 —— 位运算实现</h2><p>注意：两个数一定不能指向同一内存空间，不然结果都会变成0！</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"keyword\">int</span> a,b;</span><br><span class=\"line\">a = a^b;</span><br><span class=\"line\">b = a^b;</span><br><span class=\"line\">a = a^b;</span><br></pre></td></tr></table></figure>\n\n<p>二进制异或运算 0^1 , 0^0 , 1^1 。相同为 0 ，不同为 1 。</p>\n<p>运用到具体两个数字上，就是相同两数异或会为 0 ， 0 再异或任何一个非零的数，就是这个数本身。</p>\n<p>异或有交换律和结合律。</p>\n<h2 id=\"运用实战\"><a href=\"#运用实战\" class=\"headerlink\" title=\"运用实战\"></a>运用实战</h2><h3 id=\"问题1\"><a href=\"#问题1\" class=\"headerlink\" title=\"问题1\"></a>问题1</h3><p><strong>给一个数组 arr[] ，有一种数出现了奇数次，其它数都出现了偶数次，让你把那出现奇数次的数找出来</strong></p>\n<figure class=\"highlight plaintext\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br></pre></td><td class=\"code\"><pre><span class=\"line\">int[] arr=new int[]&#123;2,2,3,3,4,4,5,5,5&#125;;</span><br><span class=\"line\">int res=0;</span><br><span class=\"line\">for (int cur : arr) &#123;</span><br><span class=\"line\">    res ^=cur;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\">return res;</span><br></pre></td></tr></table></figure>\n\n<p><strong>给一个数组 arr[] ，有两种数出现了奇数次，其它数都出现了偶数次，让你把那出现奇数次的两种数找出来</strong></p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"></span><br><span class=\"line\"><span class=\"keyword\">int</span>[] arr = <span class=\"keyword\">new</span> <span class=\"keyword\">int</span>[]&#123;<span class=\"number\">2</span>, <span class=\"number\">2</span>, <span class=\"number\">3</span>, <span class=\"number\">3</span>, <span class=\"number\">4</span>, <span class=\"number\">4</span>, <span class=\"number\">5</span>, <span class=\"number\">5</span>, <span class=\"number\">5</span>, <span class=\"number\">6</span>, <span class=\"number\">6</span>, <span class=\"number\">6</span>&#125;;</span><br><span class=\"line\"><span class=\"keyword\">int</span> eor = <span class=\"number\">0</span>;</span><br><span class=\"line\"><span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> cur : arr) &#123;</span><br><span class=\"line\">    eor ^= cur;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"><span class=\"comment\">//eor=a^b</span></span><br><span class=\"line\"><span class=\"comment\">//eor!=0</span></span><br><span class=\"line\"><span class=\"comment\">//eor必然有一个位置为1</span></span><br><span class=\"line\"><span class=\"keyword\">int</span> rightOne = eor &amp; (~eor + <span class=\"number\">1</span>);<span class=\"comment\">//提取出最右的1</span></span><br><span class=\"line\"><span class=\"keyword\">int</span> onlyOne = <span class=\"number\">0</span>;</span><br><span class=\"line\"><span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> cur : arr) &#123;</span><br><span class=\"line\">    <span class=\"keyword\">if</span> ((rightOne &amp; cur) == <span class=\"number\">0</span>) &#123; <span class=\"comment\">//与运算。最右的 1 只有与上 1 才能等于 1 。</span></span><br><span class=\"line\">        onlyOne ^= cur;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\">&#125;<span class=\"comment\">//把其中一个数提取出来了 onlyOne = a || b</span></span><br><span class=\"line\">System.out.println(onlyOne + <span class=\"string\">&quot; &quot;</span> + (eor ^ onlyOne));</span><br></pre></td></tr></table></figure>\n\n<ul>\n<li>与运算。只有两个位都等于 1 时，结果才为 1</li>\n<li>或运算。只要有 1 个位为 1 ，结果就为 1</li>\n<li>异或运算。如果两个位为“异”（值不同），结果就为 1 。</li>\n</ul>\n<h2 id=\"时间复杂度\"><a href=\"#时间复杂度\" class=\"headerlink\" title=\"时间复杂度\"></a>时间复杂度</h2><p>算法在<strong>最坏情况</strong>下运行所需时间。</p>\n"},{"title":"桶排序入门","date":"2021-06-19T06:48:11.000Z","_content":"\n## 原理\n\n桶排序是一个排序算法，原理是将数组分到有限数量的桶里。每个桶再个别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序）。\n\n桶排序以下列程序进行：\n1. 设置一个定量的数组当作空桶子。\n2. 寻访序列，并且把项目一个一个放到对应的桶子里。\n3. 对每个不是空的桶子进行排序。\n4. 从不是空的桶子里把项目再放回原来的序列中。\n\n![image.png](https://gitee.com/missingnine/own-image-store/raw/master/202106/bucket-sort1.png)\n![image.png](https://gitee.com/missingnine/own-image-store/raw/master/202106/bucket-sort2.png)\n\n> 把数组的一组数按照 0-9，10-19， 20-29 这种规律进行分组，也就是分桶。\n>\n> 再在每一个桶里将数字进行排序。\n\n## 从简单入门\n王老师的补习班一共教 5 位小朋友，王老师让这 5 位小朋友做了一道 10 分智力算法题，5 位小朋友分别获得了不同的分数：7，5，7，8，7，5。现在需要将这 5 个分数按照从小到大的顺序打印出来。\n\n首先，我们初始化一个长度为 11 的数组 score[]，0-10 的位置分别对应 10 分的分数。\n\n于是，我们可以得到这样一个数组：\n\n```java\nscore[0]=0;//没有小朋友得过 0 分\nscore[1]=0;//没有小朋友得过 1 分\nscore[2]=0;//没有小朋友得过 2 分\nscore[3]=0;//没有小朋友得过 3 分\nscore[4]=0;//没有小朋友得过 4 分\nscore[5]=2;//有 2 个小朋友得过 5 分\nscore[6]=0;//没有小朋友得过 6 分\nscore[7]=3;//有 3 个小朋友得过 7 分\nscore[8]=1;//有 1 个小朋友得过 8 分\nscore[9]=0;//没有小朋友得过 9 分\nscore[10]=0;//没有小朋友得过 10 分\n```\n\n最终，我们只要顺序遍历这个数组，值为 0 的就不打印位置，值不为 0 就打印出来数组代表的分数：\n\n\n```java\n// score[0]~score[4] 都不打印\n5,5 //score[5]=2, 有 2 个小朋友得过 5 分\n// score[6]=0，不打印\n7，7，7 //score[7]=3，有 3 个小朋友得过 7 分\n8 //score[8]=1，有 1 个小朋友得过 8 分\n// score[9], score[10]=0，不打印\n```\n\n这里就是把数组的每个位置当作一个桶，每种分数的获得人数就是数组元素。这种是最简易版的桶排序算法的实现。但是真正的桶排序算法是比这种复杂多了。这个小示例只是作为入门的理解之用。\n","source":"_posts/算法/桶排序介绍.md","raw":"---\ntitle: 桶排序入门\ndate: 2021-06-19 14:48:11\ntags: [算法,排序]\ncategories: 算法\n---\n\n## 原理\n\n桶排序是一个排序算法，原理是将数组分到有限数量的桶里。每个桶再个别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序）。\n\n桶排序以下列程序进行：\n1. 设置一个定量的数组当作空桶子。\n2. 寻访序列，并且把项目一个一个放到对应的桶子里。\n3. 对每个不是空的桶子进行排序。\n4. 从不是空的桶子里把项目再放回原来的序列中。\n\n![image.png](https://gitee.com/missingnine/own-image-store/raw/master/202106/bucket-sort1.png)\n![image.png](https://gitee.com/missingnine/own-image-store/raw/master/202106/bucket-sort2.png)\n\n> 把数组的一组数按照 0-9，10-19， 20-29 这种规律进行分组，也就是分桶。\n>\n> 再在每一个桶里将数字进行排序。\n\n## 从简单入门\n王老师的补习班一共教 5 位小朋友，王老师让这 5 位小朋友做了一道 10 分智力算法题，5 位小朋友分别获得了不同的分数：7，5，7，8，7，5。现在需要将这 5 个分数按照从小到大的顺序打印出来。\n\n首先，我们初始化一个长度为 11 的数组 score[]，0-10 的位置分别对应 10 分的分数。\n\n于是，我们可以得到这样一个数组：\n\n```java\nscore[0]=0;//没有小朋友得过 0 分\nscore[1]=0;//没有小朋友得过 1 分\nscore[2]=0;//没有小朋友得过 2 分\nscore[3]=0;//没有小朋友得过 3 分\nscore[4]=0;//没有小朋友得过 4 分\nscore[5]=2;//有 2 个小朋友得过 5 分\nscore[6]=0;//没有小朋友得过 6 分\nscore[7]=3;//有 3 个小朋友得过 7 分\nscore[8]=1;//有 1 个小朋友得过 8 分\nscore[9]=0;//没有小朋友得过 9 分\nscore[10]=0;//没有小朋友得过 10 分\n```\n\n最终，我们只要顺序遍历这个数组，值为 0 的就不打印位置，值不为 0 就打印出来数组代表的分数：\n\n\n```java\n// score[0]~score[4] 都不打印\n5,5 //score[5]=2, 有 2 个小朋友得过 5 分\n// score[6]=0，不打印\n7，7，7 //score[7]=3，有 3 个小朋友得过 7 分\n8 //score[8]=1，有 1 个小朋友得过 8 分\n// score[9], score[10]=0，不打印\n```\n\n这里就是把数组的每个位置当作一个桶，每种分数的获得人数就是数组元素。这种是最简易版的桶排序算法的实现。但是真正的桶排序算法是比这种复杂多了。这个小示例只是作为入门的理解之用。\n","slug":"算法/桶排序介绍","published":1,"updated":"2022-01-28T13:15:02.941Z","comments":1,"layout":"post","photos":[],"link":"","_id":"ckyzjvxo0000ssdwohsmpg1kv","content":"<h2 id=\"原理\"><a href=\"#原理\" class=\"headerlink\" title=\"原理\"></a>原理</h2><p>桶排序是一个排序算法，原理是将数组分到有限数量的桶里。每个桶再个别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序）。</p>\n<p>桶排序以下列程序进行：</p>\n<ol>\n<li>设置一个定量的数组当作空桶子。</li>\n<li>寻访序列，并且把项目一个一个放到对应的桶子里。</li>\n<li>对每个不是空的桶子进行排序。</li>\n<li>从不是空的桶子里把项目再放回原来的序列中。</li>\n</ol>\n<p><img src=\"https://gitee.com/missingnine/own-image-store/raw/master/202106/bucket-sort1.png\" class=\"lazyload placeholder\" data-srcset=\"https://gitee.com/missingnine/own-image-store/raw/master/202106/bucket-sort1.png\" srcset=\"https://img2.baidu.com/it/u=2037979560,2772131037&fm=26&fmt=auto&gp=0.jpg\" alt=\"image.png\"><br><img src=\"https://gitee.com/missingnine/own-image-store/raw/master/202106/bucket-sort2.png\" class=\"lazyload placeholder\" data-srcset=\"https://gitee.com/missingnine/own-image-store/raw/master/202106/bucket-sort2.png\" srcset=\"https://img2.baidu.com/it/u=2037979560,2772131037&fm=26&fmt=auto&gp=0.jpg\" alt=\"image.png\"></p>\n<blockquote>\n<p>把数组的一组数按照 0-9，10-19， 20-29 这种规律进行分组，也就是分桶。</p>\n<p>再在每一个桶里将数字进行排序。</p>\n</blockquote>\n<h2 id=\"从简单入门\"><a href=\"#从简单入门\" class=\"headerlink\" title=\"从简单入门\"></a>从简单入门</h2><p>王老师的补习班一共教 5 位小朋友，王老师让这 5 位小朋友做了一道 10 分智力算法题，5 位小朋友分别获得了不同的分数：7，5，7，8，7，5。现在需要将这 5 个分数按照从小到大的顺序打印出来。</p>\n<p>首先，我们初始化一个长度为 11 的数组 score[]，0-10 的位置分别对应 10 分的分数。</p>\n<p>于是，我们可以得到这样一个数组：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br></pre></td><td class=\"code\"><pre><span class=\"line\">score[<span class=\"number\">0</span>]=<span class=\"number\">0</span>;<span class=\"comment\">//没有小朋友得过 0 分</span></span><br><span class=\"line\">score[<span class=\"number\">1</span>]=<span class=\"number\">0</span>;<span class=\"comment\">//没有小朋友得过 1 分</span></span><br><span class=\"line\">score[<span class=\"number\">2</span>]=<span class=\"number\">0</span>;<span class=\"comment\">//没有小朋友得过 2 分</span></span><br><span class=\"line\">score[<span class=\"number\">3</span>]=<span class=\"number\">0</span>;<span class=\"comment\">//没有小朋友得过 3 分</span></span><br><span class=\"line\">score[<span class=\"number\">4</span>]=<span class=\"number\">0</span>;<span class=\"comment\">//没有小朋友得过 4 分</span></span><br><span class=\"line\">score[<span class=\"number\">5</span>]=<span class=\"number\">2</span>;<span class=\"comment\">//有 2 个小朋友得过 5 分</span></span><br><span class=\"line\">score[<span class=\"number\">6</span>]=<span class=\"number\">0</span>;<span class=\"comment\">//没有小朋友得过 6 分</span></span><br><span class=\"line\">score[<span class=\"number\">7</span>]=<span class=\"number\">3</span>;<span class=\"comment\">//有 3 个小朋友得过 7 分</span></span><br><span class=\"line\">score[<span class=\"number\">8</span>]=<span class=\"number\">1</span>;<span class=\"comment\">//有 1 个小朋友得过 8 分</span></span><br><span class=\"line\">score[<span class=\"number\">9</span>]=<span class=\"number\">0</span>;<span class=\"comment\">//没有小朋友得过 9 分</span></span><br><span class=\"line\">score[<span class=\"number\">10</span>]=<span class=\"number\">0</span>;<span class=\"comment\">//没有小朋友得过 10 分</span></span><br></pre></td></tr></table></figure>\n\n<p>最终，我们只要顺序遍历这个数组，值为 0 的就不打印位置，值不为 0 就打印出来数组代表的分数：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"comment\">// score[0]~score[4] 都不打印</span></span><br><span class=\"line\"><span class=\"number\">5</span>,<span class=\"number\">5</span> <span class=\"comment\">//score[5]=2, 有 2 个小朋友得过 5 分</span></span><br><span class=\"line\"><span class=\"comment\">// score[6]=0，不打印</span></span><br><span class=\"line\"><span class=\"number\">7</span>，<span class=\"number\">7</span>，<span class=\"number\">7</span> <span class=\"comment\">//score[7]=3，有 3 个小朋友得过 7 分</span></span><br><span class=\"line\"><span class=\"number\">8</span> <span class=\"comment\">//score[8]=1，有 1 个小朋友得过 8 分</span></span><br><span class=\"line\"><span class=\"comment\">// score[9], score[10]=0，不打印</span></span><br></pre></td></tr></table></figure>\n\n<p>这里就是把数组的每个位置当作一个桶，每种分数的获得人数就是数组元素。这种是最简易版的桶排序算法的实现。但是真正的桶排序算法是比这种复杂多了。这个小示例只是作为入门的理解之用。</p>\n","site":{"data":{}},"excerpt":"","more":"<h2 id=\"原理\"><a href=\"#原理\" class=\"headerlink\" title=\"原理\"></a>原理</h2><p>桶排序是一个排序算法，原理是将数组分到有限数量的桶里。每个桶再个别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序）。</p>\n<p>桶排序以下列程序进行：</p>\n<ol>\n<li>设置一个定量的数组当作空桶子。</li>\n<li>寻访序列，并且把项目一个一个放到对应的桶子里。</li>\n<li>对每个不是空的桶子进行排序。</li>\n<li>从不是空的桶子里把项目再放回原来的序列中。</li>\n</ol>\n<p><img src=\"https://gitee.com/missingnine/own-image-store/raw/master/202106/bucket-sort1.png\" alt=\"image.png\"><br><img src=\"https://gitee.com/missingnine/own-image-store/raw/master/202106/bucket-sort2.png\" alt=\"image.png\"></p>\n<blockquote>\n<p>把数组的一组数按照 0-9，10-19， 20-29 这种规律进行分组，也就是分桶。</p>\n<p>再在每一个桶里将数字进行排序。</p>\n</blockquote>\n<h2 id=\"从简单入门\"><a href=\"#从简单入门\" class=\"headerlink\" title=\"从简单入门\"></a>从简单入门</h2><p>王老师的补习班一共教 5 位小朋友，王老师让这 5 位小朋友做了一道 10 分智力算法题，5 位小朋友分别获得了不同的分数：7，5，7，8，7，5。现在需要将这 5 个分数按照从小到大的顺序打印出来。</p>\n<p>首先，我们初始化一个长度为 11 的数组 score[]，0-10 的位置分别对应 10 分的分数。</p>\n<p>于是，我们可以得到这样一个数组：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br></pre></td><td class=\"code\"><pre><span class=\"line\">score[<span class=\"number\">0</span>]=<span class=\"number\">0</span>;<span class=\"comment\">//没有小朋友得过 0 分</span></span><br><span class=\"line\">score[<span class=\"number\">1</span>]=<span class=\"number\">0</span>;<span class=\"comment\">//没有小朋友得过 1 分</span></span><br><span class=\"line\">score[<span class=\"number\">2</span>]=<span class=\"number\">0</span>;<span class=\"comment\">//没有小朋友得过 2 分</span></span><br><span class=\"line\">score[<span class=\"number\">3</span>]=<span class=\"number\">0</span>;<span class=\"comment\">//没有小朋友得过 3 分</span></span><br><span class=\"line\">score[<span class=\"number\">4</span>]=<span class=\"number\">0</span>;<span class=\"comment\">//没有小朋友得过 4 分</span></span><br><span class=\"line\">score[<span class=\"number\">5</span>]=<span class=\"number\">2</span>;<span class=\"comment\">//有 2 个小朋友得过 5 分</span></span><br><span class=\"line\">score[<span class=\"number\">6</span>]=<span class=\"number\">0</span>;<span class=\"comment\">//没有小朋友得过 6 分</span></span><br><span class=\"line\">score[<span class=\"number\">7</span>]=<span class=\"number\">3</span>;<span class=\"comment\">//有 3 个小朋友得过 7 分</span></span><br><span class=\"line\">score[<span class=\"number\">8</span>]=<span class=\"number\">1</span>;<span class=\"comment\">//有 1 个小朋友得过 8 分</span></span><br><span class=\"line\">score[<span class=\"number\">9</span>]=<span class=\"number\">0</span>;<span class=\"comment\">//没有小朋友得过 9 分</span></span><br><span class=\"line\">score[<span class=\"number\">10</span>]=<span class=\"number\">0</span>;<span class=\"comment\">//没有小朋友得过 10 分</span></span><br></pre></td></tr></table></figure>\n\n<p>最终，我们只要顺序遍历这个数组，值为 0 的就不打印位置，值不为 0 就打印出来数组代表的分数：</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"comment\">// score[0]~score[4] 都不打印</span></span><br><span class=\"line\"><span class=\"number\">5</span>,<span class=\"number\">5</span> <span class=\"comment\">//score[5]=2, 有 2 个小朋友得过 5 分</span></span><br><span class=\"line\"><span class=\"comment\">// score[6]=0，不打印</span></span><br><span class=\"line\"><span class=\"number\">7</span>，<span class=\"number\">7</span>，<span class=\"number\">7</span> <span class=\"comment\">//score[7]=3，有 3 个小朋友得过 7 分</span></span><br><span class=\"line\"><span class=\"number\">8</span> <span class=\"comment\">//score[8]=1，有 1 个小朋友得过 8 分</span></span><br><span class=\"line\"><span class=\"comment\">// score[9], score[10]=0，不打印</span></span><br></pre></td></tr></table></figure>\n\n<p>这里就是把数组的每个位置当作一个桶，每种分数的获得人数就是数组元素。这种是最简易版的桶排序算法的实现。但是真正的桶排序算法是比这种复杂多了。这个小示例只是作为入门的理解之用。</p>\n"},{"title":"选择排序","date":"2021-06-19T03:11:30.000Z","_content":"\n相对于冒泡排序，选择排序多一个变量，专门存储最小值、最大值的下标，等每轮次循环遍历结束后，才会进行两个元素的交换。这样比冒泡排序减少了交换次数。\n\n![SEL.gif](https://gitee.com/missingnine/own-image-store/raw/master/202106/SEL.gif)\n\n#### 1. 基本实现\n\n```java\npublic static void main(String[] args) {\n    int[] arr = new int[]{189, -6, 0, 1, 34, 78};\n    selectionSort(arr);\n    Arrays.stream(arr).forEach(System.out::println);\n}\n\npublic static void selectionSort(int[] arr) {\n    int count = 0, length = arr.length, minIndex;\n    for (int i = 0; i < length - 1; i++) {\n        minIndex = i;\n        for (int j = i + 1; j < length; j++) {\n            if (arr[minIndex] > arr[j]) {\n                minIndex = j;\n            }\n            count++;\n        }\n        int temp = arr[i];\n        arr[i] = arr[minIndex];\n        arr[minIndex] = temp;\n    }\n    System.out.println(\"循环进行了 \" + count + \" 次\");\n}\n\npublic static void swap(int[] arr, int i, int j) {\n    int temp = arr[i];\n    arr[i] = arr[j];\n    arr[j] = temp;\n}\n\n//output\n循环进行了 15 次\n-6\n0\n1\n34\n78\n189\n\nProcess finished with exit code 0\n\n```\n#### 2. 优化版本1\n既然每轮遍历时找出了最小值，同时把最大值也顺便找出来。这就是二元选择排序的思想。\n\n使用二元选择排序，每轮选择时记录最小值和最大值，可以把数组需要遍历的范围缩小一倍。\n\n```java\n\npublic static void main(String[] args) {\n    int[] arr = new int[]{189, -6, 0, 1, 34, 78};\n    selectionSort(arr);\n    Arrays.stream(arr).forEach(System.out::println);\n}\n\npublic static void selectionSort(int[] arr) {\n    int minIndex, maxIndex,count=0;\n    for (int i = 0; i < arr.length / 2; i++) {\n        minIndex = i;\n        maxIndex = i;\n        for (int j = i + 1; j < arr.length - i; j++) {\n            if (arr[minIndex] > arr[j]) {\n                minIndex = j;\n            }\n            if (arr[maxIndex] < arr[j]) {\n                maxIndex = j;\n            }\n            count++;\n        }\n        if (minIndex == maxIndex) break;\n        int temp = arr[i];\n        arr[i] = arr[minIndex];\n        arr[minIndex] = temp;\n        if (maxIndex == i) maxIndex = minIndex;\n        int lastIndex = arr.length - 1 - i;\n        temp = arr[lastIndex];\n        arr[lastIndex] = arr[maxIndex];\n        arr[maxIndex] = temp;\n    }\n    System.out.println(\"循环进行了 \" + count + \" 次\");\n}\n\npublic static void swap(int[] arr, int i, int j) {\n    int temp = arr[i];\n    arr[i] = arr[j];\n    arr[j] = temp;\n}\n\n//output\n循环进行了 9 次\n-6\n0\n1\n34\n78\n189\n\nProcess finished with exit code 0\n\n```\n#### 总结\n从代码可以看出，虽然二元选择排序最外层的遍历范围缩小了，但 for 循环内做的事情翻了一倍。也就是说二元选择排序无法将选择排序的效率提升一倍。但实测会发现二元选择排序的速度确实比选择排序的速度快一点点。\n","source":"_posts/算法/选择排序.md","raw":"---\ntitle: 选择排序\ndate: 2021-06-19 11:11:30\ntag: [算法,排序]\ncategories: 算法\n---\n\n相对于冒泡排序，选择排序多一个变量，专门存储最小值、最大值的下标，等每轮次循环遍历结束后，才会进行两个元素的交换。这样比冒泡排序减少了交换次数。\n\n![SEL.gif](https://gitee.com/missingnine/own-image-store/raw/master/202106/SEL.gif)\n\n#### 1. 基本实现\n\n```java\npublic static void main(String[] args) {\n    int[] arr = new int[]{189, -6, 0, 1, 34, 78};\n    selectionSort(arr);\n    Arrays.stream(arr).forEach(System.out::println);\n}\n\npublic static void selectionSort(int[] arr) {\n    int count = 0, length = arr.length, minIndex;\n    for (int i = 0; i < length - 1; i++) {\n        minIndex = i;\n        for (int j = i + 1; j < length; j++) {\n            if (arr[minIndex] > arr[j]) {\n                minIndex = j;\n            }\n            count++;\n        }\n        int temp = arr[i];\n        arr[i] = arr[minIndex];\n        arr[minIndex] = temp;\n    }\n    System.out.println(\"循环进行了 \" + count + \" 次\");\n}\n\npublic static void swap(int[] arr, int i, int j) {\n    int temp = arr[i];\n    arr[i] = arr[j];\n    arr[j] = temp;\n}\n\n//output\n循环进行了 15 次\n-6\n0\n1\n34\n78\n189\n\nProcess finished with exit code 0\n\n```\n#### 2. 优化版本1\n既然每轮遍历时找出了最小值，同时把最大值也顺便找出来。这就是二元选择排序的思想。\n\n使用二元选择排序，每轮选择时记录最小值和最大值，可以把数组需要遍历的范围缩小一倍。\n\n```java\n\npublic static void main(String[] args) {\n    int[] arr = new int[]{189, -6, 0, 1, 34, 78};\n    selectionSort(arr);\n    Arrays.stream(arr).forEach(System.out::println);\n}\n\npublic static void selectionSort(int[] arr) {\n    int minIndex, maxIndex,count=0;\n    for (int i = 0; i < arr.length / 2; i++) {\n        minIndex = i;\n        maxIndex = i;\n        for (int j = i + 1; j < arr.length - i; j++) {\n            if (arr[minIndex] > arr[j]) {\n                minIndex = j;\n            }\n            if (arr[maxIndex] < arr[j]) {\n                maxIndex = j;\n            }\n            count++;\n        }\n        if (minIndex == maxIndex) break;\n        int temp = arr[i];\n        arr[i] = arr[minIndex];\n        arr[minIndex] = temp;\n        if (maxIndex == i) maxIndex = minIndex;\n        int lastIndex = arr.length - 1 - i;\n        temp = arr[lastIndex];\n        arr[lastIndex] = arr[maxIndex];\n        arr[maxIndex] = temp;\n    }\n    System.out.println(\"循环进行了 \" + count + \" 次\");\n}\n\npublic static void swap(int[] arr, int i, int j) {\n    int temp = arr[i];\n    arr[i] = arr[j];\n    arr[j] = temp;\n}\n\n//output\n循环进行了 9 次\n-6\n0\n1\n34\n78\n189\n\nProcess finished with exit code 0\n\n```\n#### 总结\n从代码可以看出，虽然二元选择排序最外层的遍历范围缩小了，但 for 循环内做的事情翻了一倍。也就是说二元选择排序无法将选择排序的效率提升一倍。但实测会发现二元选择排序的速度确实比选择排序的速度快一点点。\n","slug":"算法/选择排序","published":1,"updated":"2022-01-28T13:15:02.941Z","comments":1,"layout":"post","photos":[],"link":"","_id":"ckyzjvxoc0023sdwo3s119l9u","content":"<p>相对于冒泡排序，选择排序多一个变量，专门存储最小值、最大值的下标，等每轮次循环遍历结束后，才会进行两个元素的交换。这样比冒泡排序减少了交换次数。</p>\n<p><img src=\"https://gitee.com/missingnine/own-image-store/raw/master/202106/SEL.gif\" class=\"lazyload placeholder\" data-srcset=\"https://gitee.com/missingnine/own-image-store/raw/master/202106/SEL.gif\" srcset=\"https://img2.baidu.com/it/u=2037979560,2772131037&fm=26&fmt=auto&gp=0.jpg\" alt=\"SEL.gif\"></p>\n<h4 id=\"1-基本实现\"><a href=\"#1-基本实现\" class=\"headerlink\" title=\"1. 基本实现\"></a>1. 基本实现</h4><figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br><span class=\"line\">31</span><br><span class=\"line\">32</span><br><span class=\"line\">33</span><br><span class=\"line\">34</span><br><span class=\"line\">35</span><br><span class=\"line\">36</span><br><span class=\"line\">37</span><br><span class=\"line\">38</span><br><span class=\"line\">39</span><br><span class=\"line\">40</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">main</span><span class=\"params\">(String[] args)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span>[] arr = <span class=\"keyword\">new</span> <span class=\"keyword\">int</span>[]&#123;<span class=\"number\">189</span>, -<span class=\"number\">6</span>, <span class=\"number\">0</span>, <span class=\"number\">1</span>, <span class=\"number\">34</span>, <span class=\"number\">78</span>&#125;;</span><br><span class=\"line\">    selectionSort(arr);</span><br><span class=\"line\">    Arrays.stream(arr).forEach(System.out::println);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">selectionSort</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> count = <span class=\"number\">0</span>, length = arr.length, minIndex;</span><br><span class=\"line\">    <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> i = <span class=\"number\">0</span>; i &lt; length - <span class=\"number\">1</span>; i++) &#123;</span><br><span class=\"line\">        minIndex = i;</span><br><span class=\"line\">        <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> j = i + <span class=\"number\">1</span>; j &lt; length; j++) &#123;</span><br><span class=\"line\">            <span class=\"keyword\">if</span> (arr[minIndex] &gt; arr[j]) &#123;</span><br><span class=\"line\">                minIndex = j;</span><br><span class=\"line\">            &#125;</span><br><span class=\"line\">            count++;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">        <span class=\"keyword\">int</span> temp = arr[i];</span><br><span class=\"line\">        arr[i] = arr[minIndex];</span><br><span class=\"line\">        arr[minIndex] = temp;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\">    System.out.println(<span class=\"string\">&quot;循环进行了 &quot;</span> + count + <span class=\"string\">&quot; 次&quot;</span>);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">swap</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr, <span class=\"keyword\">int</span> i, <span class=\"keyword\">int</span> j)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> temp = arr[i];</span><br><span class=\"line\">    arr[i] = arr[j];</span><br><span class=\"line\">    arr[j] = temp;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"comment\">//output</span></span><br><span class=\"line\">循环进行了 <span class=\"number\">15</span> 次</span><br><span class=\"line\">-<span class=\"number\">6</span></span><br><span class=\"line\"><span class=\"number\">0</span></span><br><span class=\"line\"><span class=\"number\">1</span></span><br><span class=\"line\"><span class=\"number\">34</span></span><br><span class=\"line\"><span class=\"number\">78</span></span><br><span class=\"line\"><span class=\"number\">189</span></span><br><span class=\"line\"></span><br><span class=\"line\">Process finished with exit code <span class=\"number\">0</span></span><br><span class=\"line\"></span><br></pre></td></tr></table></figure>\n<h4 id=\"2-优化版本1\"><a href=\"#2-优化版本1\" class=\"headerlink\" title=\"2. 优化版本1\"></a>2. 优化版本1</h4><p>既然每轮遍历时找出了最小值，同时把最大值也顺便找出来。这就是二元选择排序的思想。</p>\n<p>使用二元选择排序，每轮选择时记录最小值和最大值，可以把数组需要遍历的范围缩小一倍。</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br><span class=\"line\">31</span><br><span class=\"line\">32</span><br><span class=\"line\">33</span><br><span class=\"line\">34</span><br><span class=\"line\">35</span><br><span class=\"line\">36</span><br><span class=\"line\">37</span><br><span class=\"line\">38</span><br><span class=\"line\">39</span><br><span class=\"line\">40</span><br><span class=\"line\">41</span><br><span class=\"line\">42</span><br><span class=\"line\">43</span><br><span class=\"line\">44</span><br><span class=\"line\">45</span><br><span class=\"line\">46</span><br><span class=\"line\">47</span><br><span class=\"line\">48</span><br><span class=\"line\">49</span><br><span class=\"line\">50</span><br><span class=\"line\">51</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">main</span><span class=\"params\">(String[] args)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span>[] arr = <span class=\"keyword\">new</span> <span class=\"keyword\">int</span>[]&#123;<span class=\"number\">189</span>, -<span class=\"number\">6</span>, <span class=\"number\">0</span>, <span class=\"number\">1</span>, <span class=\"number\">34</span>, <span class=\"number\">78</span>&#125;;</span><br><span class=\"line\">    selectionSort(arr);</span><br><span class=\"line\">    Arrays.stream(arr).forEach(System.out::println);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">selectionSort</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> minIndex, maxIndex,count=<span class=\"number\">0</span>;</span><br><span class=\"line\">    <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> i = <span class=\"number\">0</span>; i &lt; arr.length / <span class=\"number\">2</span>; i++) &#123;</span><br><span class=\"line\">        minIndex = i;</span><br><span class=\"line\">        maxIndex = i;</span><br><span class=\"line\">        <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> j = i + <span class=\"number\">1</span>; j &lt; arr.length - i; j++) &#123;</span><br><span class=\"line\">            <span class=\"keyword\">if</span> (arr[minIndex] &gt; arr[j]) &#123;</span><br><span class=\"line\">                minIndex = j;</span><br><span class=\"line\">            &#125;</span><br><span class=\"line\">            <span class=\"keyword\">if</span> (arr[maxIndex] &lt; arr[j]) &#123;</span><br><span class=\"line\">                maxIndex = j;</span><br><span class=\"line\">            &#125;</span><br><span class=\"line\">            count++;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">        <span class=\"keyword\">if</span> (minIndex == maxIndex) <span class=\"keyword\">break</span>;</span><br><span class=\"line\">        <span class=\"keyword\">int</span> temp = arr[i];</span><br><span class=\"line\">        arr[i] = arr[minIndex];</span><br><span class=\"line\">        arr[minIndex] = temp;</span><br><span class=\"line\">        <span class=\"keyword\">if</span> (maxIndex == i) maxIndex = minIndex;</span><br><span class=\"line\">        <span class=\"keyword\">int</span> lastIndex = arr.length - <span class=\"number\">1</span> - i;</span><br><span class=\"line\">        temp = arr[lastIndex];</span><br><span class=\"line\">        arr[lastIndex] = arr[maxIndex];</span><br><span class=\"line\">        arr[maxIndex] = temp;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\">    System.out.println(<span class=\"string\">&quot;循环进行了 &quot;</span> + count + <span class=\"string\">&quot; 次&quot;</span>);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">swap</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr, <span class=\"keyword\">int</span> i, <span class=\"keyword\">int</span> j)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> temp = arr[i];</span><br><span class=\"line\">    arr[i] = arr[j];</span><br><span class=\"line\">    arr[j] = temp;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"comment\">//output</span></span><br><span class=\"line\">循环进行了 <span class=\"number\">9</span> 次</span><br><span class=\"line\">-<span class=\"number\">6</span></span><br><span class=\"line\"><span class=\"number\">0</span></span><br><span class=\"line\"><span class=\"number\">1</span></span><br><span class=\"line\"><span class=\"number\">34</span></span><br><span class=\"line\"><span class=\"number\">78</span></span><br><span class=\"line\"><span class=\"number\">189</span></span><br><span class=\"line\"></span><br><span class=\"line\">Process finished with exit code <span class=\"number\">0</span></span><br><span class=\"line\"></span><br></pre></td></tr></table></figure>\n<h4 id=\"总结\"><a href=\"#总结\" class=\"headerlink\" title=\"总结\"></a>总结</h4><p>从代码可以看出，虽然二元选择排序最外层的遍历范围缩小了，但 for 循环内做的事情翻了一倍。也就是说二元选择排序无法将选择排序的效率提升一倍。但实测会发现二元选择排序的速度确实比选择排序的速度快一点点。</p>\n","site":{"data":{}},"excerpt":"","more":"<p>相对于冒泡排序，选择排序多一个变量，专门存储最小值、最大值的下标，等每轮次循环遍历结束后，才会进行两个元素的交换。这样比冒泡排序减少了交换次数。</p>\n<p><img src=\"https://gitee.com/missingnine/own-image-store/raw/master/202106/SEL.gif\" alt=\"SEL.gif\"></p>\n<h4 id=\"1-基本实现\"><a href=\"#1-基本实现\" class=\"headerlink\" title=\"1. 基本实现\"></a>1. 基本实现</h4><figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br><span class=\"line\">31</span><br><span class=\"line\">32</span><br><span class=\"line\">33</span><br><span class=\"line\">34</span><br><span class=\"line\">35</span><br><span class=\"line\">36</span><br><span class=\"line\">37</span><br><span class=\"line\">38</span><br><span class=\"line\">39</span><br><span class=\"line\">40</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">main</span><span class=\"params\">(String[] args)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span>[] arr = <span class=\"keyword\">new</span> <span class=\"keyword\">int</span>[]&#123;<span class=\"number\">189</span>, -<span class=\"number\">6</span>, <span class=\"number\">0</span>, <span class=\"number\">1</span>, <span class=\"number\">34</span>, <span class=\"number\">78</span>&#125;;</span><br><span class=\"line\">    selectionSort(arr);</span><br><span class=\"line\">    Arrays.stream(arr).forEach(System.out::println);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">selectionSort</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> count = <span class=\"number\">0</span>, length = arr.length, minIndex;</span><br><span class=\"line\">    <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> i = <span class=\"number\">0</span>; i &lt; length - <span class=\"number\">1</span>; i++) &#123;</span><br><span class=\"line\">        minIndex = i;</span><br><span class=\"line\">        <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> j = i + <span class=\"number\">1</span>; j &lt; length; j++) &#123;</span><br><span class=\"line\">            <span class=\"keyword\">if</span> (arr[minIndex] &gt; arr[j]) &#123;</span><br><span class=\"line\">                minIndex = j;</span><br><span class=\"line\">            &#125;</span><br><span class=\"line\">            count++;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">        <span class=\"keyword\">int</span> temp = arr[i];</span><br><span class=\"line\">        arr[i] = arr[minIndex];</span><br><span class=\"line\">        arr[minIndex] = temp;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\">    System.out.println(<span class=\"string\">&quot;循环进行了 &quot;</span> + count + <span class=\"string\">&quot; 次&quot;</span>);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">swap</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr, <span class=\"keyword\">int</span> i, <span class=\"keyword\">int</span> j)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> temp = arr[i];</span><br><span class=\"line\">    arr[i] = arr[j];</span><br><span class=\"line\">    arr[j] = temp;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"comment\">//output</span></span><br><span class=\"line\">循环进行了 <span class=\"number\">15</span> 次</span><br><span class=\"line\">-<span class=\"number\">6</span></span><br><span class=\"line\"><span class=\"number\">0</span></span><br><span class=\"line\"><span class=\"number\">1</span></span><br><span class=\"line\"><span class=\"number\">34</span></span><br><span class=\"line\"><span class=\"number\">78</span></span><br><span class=\"line\"><span class=\"number\">189</span></span><br><span class=\"line\"></span><br><span class=\"line\">Process finished with exit code <span class=\"number\">0</span></span><br><span class=\"line\"></span><br></pre></td></tr></table></figure>\n<h4 id=\"2-优化版本1\"><a href=\"#2-优化版本1\" class=\"headerlink\" title=\"2. 优化版本1\"></a>2. 优化版本1</h4><p>既然每轮遍历时找出了最小值，同时把最大值也顺便找出来。这就是二元选择排序的思想。</p>\n<p>使用二元选择排序，每轮选择时记录最小值和最大值，可以把数组需要遍历的范围缩小一倍。</p>\n<figure class=\"highlight java\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br><span class=\"line\">5</span><br><span class=\"line\">6</span><br><span class=\"line\">7</span><br><span class=\"line\">8</span><br><span class=\"line\">9</span><br><span class=\"line\">10</span><br><span class=\"line\">11</span><br><span class=\"line\">12</span><br><span class=\"line\">13</span><br><span class=\"line\">14</span><br><span class=\"line\">15</span><br><span class=\"line\">16</span><br><span class=\"line\">17</span><br><span class=\"line\">18</span><br><span class=\"line\">19</span><br><span class=\"line\">20</span><br><span class=\"line\">21</span><br><span class=\"line\">22</span><br><span class=\"line\">23</span><br><span class=\"line\">24</span><br><span class=\"line\">25</span><br><span class=\"line\">26</span><br><span class=\"line\">27</span><br><span class=\"line\">28</span><br><span class=\"line\">29</span><br><span class=\"line\">30</span><br><span class=\"line\">31</span><br><span class=\"line\">32</span><br><span class=\"line\">33</span><br><span class=\"line\">34</span><br><span class=\"line\">35</span><br><span class=\"line\">36</span><br><span class=\"line\">37</span><br><span class=\"line\">38</span><br><span class=\"line\">39</span><br><span class=\"line\">40</span><br><span class=\"line\">41</span><br><span class=\"line\">42</span><br><span class=\"line\">43</span><br><span class=\"line\">44</span><br><span class=\"line\">45</span><br><span class=\"line\">46</span><br><span class=\"line\">47</span><br><span class=\"line\">48</span><br><span class=\"line\">49</span><br><span class=\"line\">50</span><br><span class=\"line\">51</span><br></pre></td><td class=\"code\"><pre><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">main</span><span class=\"params\">(String[] args)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span>[] arr = <span class=\"keyword\">new</span> <span class=\"keyword\">int</span>[]&#123;<span class=\"number\">189</span>, -<span class=\"number\">6</span>, <span class=\"number\">0</span>, <span class=\"number\">1</span>, <span class=\"number\">34</span>, <span class=\"number\">78</span>&#125;;</span><br><span class=\"line\">    selectionSort(arr);</span><br><span class=\"line\">    Arrays.stream(arr).forEach(System.out::println);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">selectionSort</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> minIndex, maxIndex,count=<span class=\"number\">0</span>;</span><br><span class=\"line\">    <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> i = <span class=\"number\">0</span>; i &lt; arr.length / <span class=\"number\">2</span>; i++) &#123;</span><br><span class=\"line\">        minIndex = i;</span><br><span class=\"line\">        maxIndex = i;</span><br><span class=\"line\">        <span class=\"keyword\">for</span> (<span class=\"keyword\">int</span> j = i + <span class=\"number\">1</span>; j &lt; arr.length - i; j++) &#123;</span><br><span class=\"line\">            <span class=\"keyword\">if</span> (arr[minIndex] &gt; arr[j]) &#123;</span><br><span class=\"line\">                minIndex = j;</span><br><span class=\"line\">            &#125;</span><br><span class=\"line\">            <span class=\"keyword\">if</span> (arr[maxIndex] &lt; arr[j]) &#123;</span><br><span class=\"line\">                maxIndex = j;</span><br><span class=\"line\">            &#125;</span><br><span class=\"line\">            count++;</span><br><span class=\"line\">        &#125;</span><br><span class=\"line\">        <span class=\"keyword\">if</span> (minIndex == maxIndex) <span class=\"keyword\">break</span>;</span><br><span class=\"line\">        <span class=\"keyword\">int</span> temp = arr[i];</span><br><span class=\"line\">        arr[i] = arr[minIndex];</span><br><span class=\"line\">        arr[minIndex] = temp;</span><br><span class=\"line\">        <span class=\"keyword\">if</span> (maxIndex == i) maxIndex = minIndex;</span><br><span class=\"line\">        <span class=\"keyword\">int</span> lastIndex = arr.length - <span class=\"number\">1</span> - i;</span><br><span class=\"line\">        temp = arr[lastIndex];</span><br><span class=\"line\">        arr[lastIndex] = arr[maxIndex];</span><br><span class=\"line\">        arr[maxIndex] = temp;</span><br><span class=\"line\">    &#125;</span><br><span class=\"line\">    System.out.println(<span class=\"string\">&quot;循环进行了 &quot;</span> + count + <span class=\"string\">&quot; 次&quot;</span>);</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"function\"><span class=\"keyword\">public</span> <span class=\"keyword\">static</span> <span class=\"keyword\">void</span> <span class=\"title\">swap</span><span class=\"params\">(<span class=\"keyword\">int</span>[] arr, <span class=\"keyword\">int</span> i, <span class=\"keyword\">int</span> j)</span> </span>&#123;</span><br><span class=\"line\">    <span class=\"keyword\">int</span> temp = arr[i];</span><br><span class=\"line\">    arr[i] = arr[j];</span><br><span class=\"line\">    arr[j] = temp;</span><br><span class=\"line\">&#125;</span><br><span class=\"line\"></span><br><span class=\"line\"><span class=\"comment\">//output</span></span><br><span class=\"line\">循环进行了 <span class=\"number\">9</span> 次</span><br><span class=\"line\">-<span class=\"number\">6</span></span><br><span class=\"line\"><span class=\"number\">0</span></span><br><span class=\"line\"><span class=\"number\">1</span></span><br><span class=\"line\"><span class=\"number\">34</span></span><br><span class=\"line\"><span class=\"number\">78</span></span><br><span class=\"line\"><span class=\"number\">189</span></span><br><span class=\"line\"></span><br><span class=\"line\">Process finished with exit code <span class=\"number\">0</span></span><br><span class=\"line\"></span><br></pre></td></tr></table></figure>\n<h4 id=\"总结\"><a href=\"#总结\" class=\"headerlink\" title=\"总结\"></a>总结</h4><p>从代码可以看出，虽然二元选择排序最外层的遍历范围缩小了，但 for 循环内做的事情翻了一倍。也就是说二元选择排序无法将选择排序的效率提升一倍。但实测会发现二元选择排序的速度确实比选择排序的速度快一点点。</p>\n"}],"PostAsset":[],"PostCategory":[{"post_id":"ckyzjvxng0001sdwo7rr6frdc","category_id":"ckyzjvxnl0004sdwo7hs48pwd","_id":"ckyzjvxnv000isdwo8ij1ce4x"},{"post_id":"ckyzjvxnk0003sdwoe4ie3jrl","category_id":"ckyzjvxnq000csdwo4hd5bmjf","_id":"ckyzjvxnz000psdwo37lh7esu"},{"post_id":"ckyzjvxnn0007sdwo8nb55hz8","category_id":"ckyzjvxnq000csdwo4hd5bmjf","_id":"ckyzjvxo1000tsdwo1n21851x"},{"post_id":"ckyzjvxno0009sdwo24r6d9uj","category_id":"ckyzjvxny000osdwofho1brak","_id":"ckyzjvxo2000ysdwo0epi9jgp"},{"post_id":"ckyzjvxnq000bsdwobqxv5gr5","category_id":"ckyzjvxny000osdwofho1brak","_id":"ckyzjvxo40012sdwo3tma5nlk"},{"post_id":"ckyzjvxns000gsdwo43ir46ht","category_id":"ckyzjvxo2000xsdwo1dua3s59","_id":"ckyzjvxo50017sdwo8x5bgovo"},{"post_id":"ckyzjvxnt000hsdwo8y1814v5","category_id":"ckyzjvxo2000xsdwo1dua3s59","_id":"ckyzjvxo6001asdwo00d81njc"},{"post_id":"ckyzjvxnx000lsdwo5mvyhu6i","category_id":"ckyzjvxo2000xsdwo1dua3s59","_id":"ckyzjvxo7001esdwo3wuydoqo"},{"post_id":"ckyzjvxny000nsdwog40geqce","category_id":"ckyzjvxo2000xsdwo1dua3s59","_id":"ckyzjvxo7001isdwo70590zds"},{"post_id":"ckyzjvxnz000rsdwo4qv0b2mk","category_id":"ckyzjvxo2000xsdwo1dua3s59","_id":"ckyzjvxo8001ksdwo5vc585dq"},{"post_id":"ckyzjvxo0000ssdwohsmpg1kv","category_id":"ckyzjvxo2000xsdwo1dua3s59","_id":"ckyzjvxo9001osdwo91p2dtv5"},{"post_id":"ckyzjvxoc0023sdwo3s119l9u","category_id":"ckyzjvxo2000xsdwo1dua3s59","_id":"ckyzjvxod0026sdwo2alq5quh"}],"PostTag":[{"post_id":"ckyzjvxng0001sdwo7rr6frdc","tag_id":"ckyzjvxnm0005sdwo6dmpgilj","_id":"ckyzjvxnr000esdwo8it5fgsi"},{"post_id":"ckyzjvxnk0003sdwoe4ie3jrl","tag_id":"ckyzjvxnr000dsdwo6hlpgxk9","_id":"ckyzjvxnx000msdwohhdxfnqp"},{"post_id":"ckyzjvxnn0007sdwo8nb55hz8","tag_id":"ckyzjvxnv000ksdwobewtg2jo","_id":"ckyzjvxo2000wsdwohyhn0kg7"},{"post_id":"ckyzjvxnn0007sdwo8nb55hz8","tag_id":"ckyzjvxnz000qsdwo4jd7dy4e","_id":"ckyzjvxo2000zsdwo6upvgvla"},{"post_id":"ckyzjvxno0009sdwo24r6d9uj","tag_id":"ckyzjvxo1000vsdwo83d08fna","_id":"ckyzjvxo40011sdwo1uyqfuzr"},{"post_id":"ckyzjvxnq000bsdwobqxv5gr5","tag_id":"ckyzjvxo20010sdwo9cc8a8cw","_id":"ckyzjvxo50015sdwo5jtf1dbg"},{"post_id":"ckyzjvxns000gsdwo43ir46ht","tag_id":"ckyzjvxo50014sdwoba0i8e3a","_id":"ckyzjvxo7001csdwoa5jkbfo1"},{"post_id":"ckyzjvxns000gsdwo43ir46ht","tag_id":"ckyzjvxo60018sdwoemid1emt","_id":"ckyzjvxo7001fsdwo808v8s4i"},{"post_id":"ckyzjvxnt000hsdwo8y1814v5","tag_id":"ckyzjvxo50014sdwoba0i8e3a","_id":"ckyzjvxo8001lsdwof8cmcnqj"},{"post_id":"ckyzjvxnt000hsdwo8y1814v5","tag_id":"ckyzjvxo7001gsdwob6ci5dzw","_id":"ckyzjvxo8001msdwodzm03guq"},{"post_id":"ckyzjvxnx000lsdwo5mvyhu6i","tag_id":"ckyzjvxo50014sdwoba0i8e3a","_id":"ckyzjvxo9001qsdwocctpa4g6"},{"post_id":"ckyzjvxnx000lsdwo5mvyhu6i","tag_id":"ckyzjvxo8001nsdwofbkf7z3a","_id":"ckyzjvxo9001rsdwo8bcq1baz"},{"post_id":"ckyzjvxny000nsdwog40geqce","tag_id":"ckyzjvxo50014sdwoba0i8e3a","_id":"ckyzjvxoa001usdwo3wuicn0l"},{"post_id":"ckyzjvxny000nsdwog40geqce","tag_id":"ckyzjvxo7001gsdwob6ci5dzw","_id":"ckyzjvxoa001vsdwo89037vvj"},{"post_id":"ckyzjvxnz000rsdwo4qv0b2mk","tag_id":"ckyzjvxo50014sdwoba0i8e3a","_id":"ckyzjvxob001ysdwogvvseorj"},{"post_id":"ckyzjvxnz000rsdwo4qv0b2mk","tag_id":"ckyzjvxoa001wsdwo9oumc04x","_id":"ckyzjvxob001zsdwo38766ks2"},{"post_id":"ckyzjvxo0000ssdwohsmpg1kv","tag_id":"ckyzjvxo50014sdwoba0i8e3a","_id":"ckyzjvxob0021sdwob5a87qxa"},{"post_id":"ckyzjvxo0000ssdwohsmpg1kv","tag_id":"ckyzjvxo7001gsdwob6ci5dzw","_id":"ckyzjvxob0022sdwod2z67nlt"},{"post_id":"ckyzjvxoc0023sdwo3s119l9u","tag_id":"ckyzjvxo50014sdwoba0i8e3a","_id":"ckyzjvxod0024sdwocmu0byns"},{"post_id":"ckyzjvxoc0023sdwo3s119l9u","tag_id":"ckyzjvxo7001gsdwob6ci5dzw","_id":"ckyzjvxod0025sdwoclkadbre"}],"Tag":[{"name":"读书","_id":"ckyzjvxnm0005sdwo6dmpgilj"},{"name":"瞎捣鼓","_id":"ckyzjvxnr000dsdwo6hlpgxk9"},{"name":"个人随笔","_id":"ckyzjvxnv000ksdwobewtg2jo"},{"name":"自制力","_id":"ckyzjvxnz000qsdwo4jd7dy4e"},{"name":"MySQL","_id":"ckyzjvxo1000vsdwo83d08fna"},{"name":"redis","_id":"ckyzjvxo20010sdwo9cc8a8cw"},{"name":"算法","_id":"ckyzjvxo50014sdwoba0i8e3a"},{"name":"刷题","_id":"ckyzjvxo60018sdwoemid1emt"},{"name":"排序","_id":"ckyzjvxo7001gsdwob6ci5dzw"},{"name":"回溯算法","_id":"ckyzjvxo8001nsdwofbkf7z3a"},{"name":"学习","_id":"ckyzjvxoa001wsdwo9oumc04x"}]}}