| comments | difficulty | edit_url | rating | source | tags | |||
|---|---|---|---|---|---|---|---|---|
true |
困难 |
2404 |
第 144 场双周赛 Q4 |
|
有一个游戏,游戏由 n x n 个房间网格状排布组成。
给你一个大小为 n x n 的二位整数数组 fruits ,其中 fruits[i][j] 表示房间 (i, j) 中的水果数目。有三个小朋友 一开始 分别从角落房间 (0, 0) ,(0, n - 1) 和 (n - 1, 0) 出发。
每一位小朋友都会 恰好 移动 n - 1 次,并到达房间 (n - 1, n - 1) :
- 从
(0, 0)出发的小朋友每次移动从房间(i, j)出发,可以到达(i + 1, j + 1),(i + 1, j)和(i, j + 1)房间之一(如果存在)。 - 从
(0, n - 1)出发的小朋友每次移动从房间(i, j)出发,可以到达房间(i + 1, j - 1),(i + 1, j)和(i + 1, j + 1)房间之一(如果存在)。 - 从
(n - 1, 0)出发的小朋友每次移动从房间(i, j)出发,可以到达房间(i - 1, j + 1),(i, j + 1)和(i + 1, j + 1)房间之一(如果存在)。
当一个小朋友到达一个房间时,会把这个房间里所有的水果都收集起来。如果有两个或者更多小朋友进入同一个房间,只有一个小朋友能收集这个房间的水果。当小朋友离开一个房间时,这个房间里不会再有水果。
请你返回三个小朋友总共 最多 可以收集多少个水果。
示例 1:
输入:fruits = [[1,2,3,4],[5,6,8,7],[9,10,11,12],[13,14,15,16]]
输出:100
解释:
这个例子中:
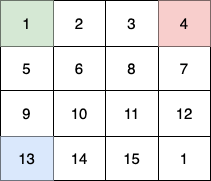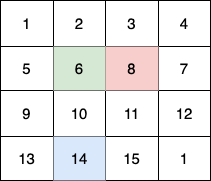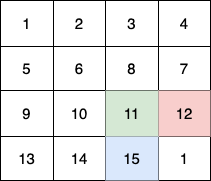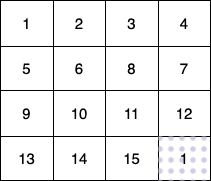
- 第 1 个小朋友(绿色)的移动路径为
(0,0) -> (1,1) -> (2,2) -> (3, 3)。 - 第 2 个小朋友(红色)的移动路径为
(0,3) -> (1,2) -> (2,3) -> (3, 3)。 - 第 3 个小朋友(蓝色)的移动路径为
(3,0) -> (3,1) -> (3,2) -> (3, 3)。
他们总共能收集 1 + 6 + 11 + 1 + 4 + 8 + 12 + 13 + 14 + 15 = 100 个水果。
示例 2:
输入:fruits = [[1,1],[1,1]]
输出:4
解释:
这个例子中:
- 第 1 个小朋友移动路径为
(0,0) -> (1,1)。 - 第 2 个小朋友移动路径为
(0,1) -> (1,1)。 - 第 3 个小朋友移动路径为
(1,0) -> (1,1)。
他们总共能收集 1 + 1 + 1 + 1 = 4 个水果。
提示:
2 <= n == fruits.length == fruits[i].length <= 10000 <= fruits[i][j] <= 1000