comments

difficulty

edit_url

2950. 可整除子串的数量 🔒

English Version

题目描述

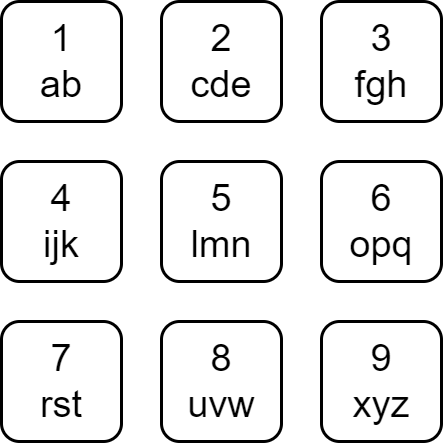
每个英文字母都被映射到一个数字，如下所示。

如果字符串的字符的映射值的总和可以被字符串的长度整除，则该字符串是 可整除 的。

给定一个字符串 s，请返回 s 的 可整除子串 的数量。

子串是字符串内的一个连续的非空字符序列。

示例 1：

Substring	Mapped	Sum	Length	Divisible?
a	1	1	1	Yes
s	7	7	1	Yes
d	2	2	1	Yes
f	3	3	1	Yes
as	1, 7	8	2	Yes
sd	7, 2	9	2	No
df	2, 3	5	2	No
asd	1, 7, 2	10	3	No
sdf	7, 2, 3	12	3	Yes
asdf	1, 7, 2, 3	13	4	No

输入：word = "asdf"
输出：6
解释：上表包含了有关 word 中每个子串的详细信息，我们可以看到其中有 6 个是可整除的。

示例 2:

输入：word = "bdh"
输出：4
解释：4 个可整除的子串是："b"，"d"，"h"，"bdh"。
可以证明 word 中没有其他可整除的子串。

示例 3:

输入：word = "abcd"
输出：6
解释：6 个可整除的子串是："a"，"b"，"c"，"d"，"ab"，"cd"。
可以证明 word 中没有其他可整除的子串。

提示：

1 <= word.length <= 2000
word 仅包含小写英文字母。

解法

方法一：枚举

我们先用一个哈希表或数组 $mp$ 记录每个字母对应的数字。

然后，我们枚举子串的起始位置 $i$，再枚举子串的结束位置 $j$，计算子串 $s[i..j]$ 的数字和 $s$，如果 $s$ 能被 $j-i+1$ 整除，那么就找到了一个可被整除的子串，将答案加一。

枚举结束后，返回答案。

时间复杂度 $O(n^2)$，空间复杂度 $O(C)$。其中 $n$ 是字符串 $word$ 的长度，而 $C$ 是字符集的大小，本题中 $C=26$。

Python3

class Solution:
    def countDivisibleSubstrings(self, word: str) -> int:
        d = ["ab", "cde", "fgh", "ijk", "lmn", "opq", "rst", "uvw", "xyz"]
        mp = {}
        for i, s in enumerate(d, 1):
            for c in s:
                mp[c] = i
        ans = 0
        n = len(word)
        for i in range(n):
            s = 0
            for j in range(i, n):
                s += mp[word[j]]
                ans += s % (j - i + 1) == 0
        return ans

Java

class Solution {
    public int countDivisibleSubstrings(String word) {
        String[] d = {"ab", "cde", "fgh", "ijk", "lmn", "opq", "rst", "uvw", "xyz"};
        int[] mp = new int[26];
        for (int i = 0; i < d.length; ++i) {
            for (char c : d[i].toCharArray()) {
                mp[c - 'a'] = i + 1;
            }
        }
        int ans = 0;
        int n = word.length();
        for (int i = 0; i < n; ++i) {
            int s = 0;
            for (int j = i; j < n; ++j) {
                s += mp[word.charAt(j) - 'a'];
                ans += s % (j - i + 1) == 0 ? 1 : 0;
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int countDivisibleSubstrings(string word) {
        string d[9] = {"ab", "cde", "fgh", "ijk", "lmn", "opq", "rst", "uvw", "xyz"};
        int mp[26]{};
        for (int i = 0; i < 9; ++i) {
            for (char& c : d[i]) {
                mp[c - 'a'] = i + 1;
            }
        }
        int ans = 0;
        int n = word.size();
        for (int i = 0; i < n; ++i) {
            int s = 0;
            for (int j = i; j < n; ++j) {
                s += mp[word[j] - 'a'];
                ans += s % (j - i + 1) == 0 ? 1 : 0;
            }
        }
        return ans;
    }
};

Go

func countDivisibleSubstrings(word string) (ans int) {
	d := []string{"ab", "cde", "fgh", "ijk", "lmn", "opq", "rst", "uvw", "xyz"}
	mp := [26]int{}
	for i, s := range d {
		for _, c := range s {
			mp[c-'a'] = i + 1
		}
	}
	n := len(word)
	for i := 0; i < n; i++ {
		s := 0
		for j := i; j < n; j++ {
			s += mp[word[j]-'a']
			if s%(j-i+1) == 0 {
				ans++
			}
		}
	}
	return
}

TypeScript

function countDivisibleSubstrings(word: string): number {
    const d: string[] = ['ab', 'cde', 'fgh', 'ijk', 'lmn', 'opq', 'rst', 'uvw', 'xyz'];
    const mp: number[] = Array(26).fill(0);
    for (let i = 0; i < d.length; ++i) {
        for (const c of d[i]) {
            mp[c.charCodeAt(0) - 'a'.charCodeAt(0)] = i + 1;
        }
    }
    const n = word.length;
    let ans = 0;
    for (let i = 0; i < n; ++i) {
        let s = 0;
        for (let j = i; j < n; ++j) {
            s += mp[word.charCodeAt(j) - 'a'.charCodeAt(0)];
            if (s % (j - i + 1) === 0) {
                ++ans;
            }
        }
    }
    return ans;
}

Rust

impl Solution {
    pub fn count_divisible_substrings(word: String) -> i32 {
        let d = vec!["ab", "cde", "fgh", "ijk", "lmn", "opq", "rst", "uvw", "xyz"];
        let mut mp = vec![0; 26];

        for (i, s) in d.iter().enumerate() {
            s.chars().for_each(|c| {
                mp[(c as usize) - ('a' as usize)] = (i + 1) as i32;
            });
        }

        let mut ans = 0;
        let n = word.len();

        for i in 0..n {
            let mut s = 0;

            for j in i..n {
                s += mp[(word.as_bytes()[j] as usize) - ('a' as usize)];
                ans += (s % ((j - i + 1) as i32) == 0) as i32;
            }
        }

        ans
    }
}

方法二：哈希表 + 前缀和 + 枚举

与方法一类似，我们先用一个哈希表或数组 $mp$ 记录每个字母对应的数字。

如果一个整数子数组的数字之和能被它的长度整除，那么这个子数组的平均值一定是一个整数。而由于子数组中每个元素的数字都在 $[1, 9]$ 范围内，因此子数组的平均值只能是 $1, 2, \cdots, 9$ 中的一个。

我们可以枚举子数组的平均值 $i$，如果一个子数组的元素和能被 $i$ 整除，假设子数组为 $a_1, a_2, \cdots, a_k$，那么 $a_1 + a_2 + \cdots + a_k = i \times k$，即 $(a_1 - i) + (a_2 - i) + \cdots + (a_k - i) = 0$。如果我们把 $a_k - i$ 视为一个新的元素 $b_k$，那么原来的子数组就变成了 $b_1, b_2, \cdots, b_k$，其中 $b_1 + b_2 + \cdots + b_k = 0$。我们只需要求出新的数组中，有多少个子数组的元素和为 $0$ 即可，这可以用“哈希表”结合“前缀和”来实现。

时间复杂度 $O(10 \times n)$，空间复杂度 $O(n)$。其中 $n$ 是字符串 $word$ 的长度。

Python3

class Solution:
    def countDivisibleSubstrings(self, word: str) -> int:
        d = ["ab", "cde", "fgh", "ijk", "lmn", "opq", "rst", "uvw", "xyz"]
        mp = {}
        for i, s in enumerate(d, 1):
            for c in s:
                mp[c] = i
        ans = 0
        for i in range(1, 10):
            cnt = defaultdict(int)
            cnt[0] = 1
            s = 0
            for c in word:
                s += mp[c] - i
                ans += cnt[s]
                cnt[s] += 1
        return ans

Java

class Solution {
    public int countDivisibleSubstrings(String word) {
        String[] d = {"ab", "cde", "fgh", "ijk", "lmn", "opq", "rst", "uvw", "xyz"};
        int[] mp = new int[26];
        for (int i = 0; i < d.length; ++i) {
            for (char c : d[i].toCharArray()) {
                mp[c - 'a'] = i + 1;
            }
        }
        int ans = 0;
        char[] cs = word.toCharArray();
        for (int i = 1; i < 10; ++i) {
            Map<Integer, Integer> cnt = new HashMap<>();
            cnt.put(0, 1);
            int s = 0;
            for (char c : cs) {
                s += mp[c - 'a'] - i;
                ans += cnt.getOrDefault(s, 0);
                cnt.merge(s, 1, Integer::sum);
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int countDivisibleSubstrings(string word) {
        string d[9] = {"ab", "cde", "fgh", "ijk", "lmn", "opq", "rst", "uvw", "xyz"};
        int mp[26]{};
        for (int i = 0; i < 9; ++i) {
            for (char& c : d[i]) {
                mp[c - 'a'] = i + 1;
            }
        }
        int ans = 0;
        for (int i = 1; i < 10; ++i) {
            unordered_map<int, int> cnt{{0, 1}};
            int s = 0;
            for (char& c : word) {
                s += mp[c - 'a'] - i;
                ans += cnt[s]++;
            }
        }
        return ans;
    }
};

Go

func countDivisibleSubstrings(word string) (ans int) {
	d := []string{"ab", "cde", "fgh", "ijk", "lmn", "opq", "rst", "uvw", "xyz"}
	mp := [26]int{}
	for i, s := range d {
		for _, c := range s {
			mp[c-'a'] = i + 1
		}
	}
	for i := 0; i < 10; i++ {
		cnt := map[int]int{0: 1}
		s := 0
		for _, c := range word {
			s += mp[c-'a'] - i
			ans += cnt[s]
			cnt[s]++
		}
	}
	return
}

TypeScript

function countDivisibleSubstrings(word: string): number {
    const d = ['ab', 'cde', 'fgh', 'ijk', 'lmn', 'opq', 'rst', 'uvw', 'xyz'];
    const mp: number[] = Array(26).fill(0);

    d.forEach((s, i) => {
        for (const c of s) {
            mp[c.charCodeAt(0) - 'a'.charCodeAt(0)] = i + 1;
        }
    });

    let ans = 0;
    for (let i = 0; i < 10; i++) {
        const cnt: { [key: number]: number } = { 0: 1 };
        let s = 0;
        for (const c of word) {
            s += mp[c.charCodeAt(0) - 'a'.charCodeAt(0)] - i;
            ans += cnt[s] || 0;
            cnt[s] = (cnt[s] || 0) + 1;
        }
    }
    return ans;
}

Rust

use std::collections::HashMap;

impl Solution {
    pub fn count_divisible_substrings(word: String) -> i32 {
        let d = vec!["ab", "cde", "fgh", "ijk", "lmn", "opq", "rst", "uvw", "xyz"];
        let mut mp: Vec<usize> = vec![0; 26];
        for (i, s) in d.iter().enumerate() {
            for c in s.chars() {
                mp[(c as usize) - ('a' as usize)] = i + 1;
            }
        }
        let mut ans = 0;
        for i in 0..10 {
            let mut cnt: HashMap<i32, i32> = HashMap::new();
            cnt.insert(0, 1);
            let mut s = 0;
            for c in word.chars() {
                s += (mp[(c as usize) - ('a' as usize)] - i) as i32;
                ans += cnt.get(&s).cloned().unwrap_or(0);
                *cnt.entry(s).or_insert(0) += 1;
            }
        }
        ans
    }
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README.md

README.md

2950. 可整除子串的数量 🔒

题目描述

解法

方法一：枚举

Python3

Java

C++

Go

TypeScript

Rust

方法二：哈希表 + 前缀和 + 枚举

Python3

Java

C++

Go

TypeScript

Rust

Files

README.md

Latest commit

History

README.md

File metadata and controls

2950. 可整除子串的数量 🔒

题目描述

解法

方法一：枚举

Python3

Java

C++

Go

TypeScript

Rust

方法二：哈希表 + 前缀和 + 枚举

Python3

Java

C++

Go

TypeScript

Rust