| comments | difficulty | edit_url | rating | source | tags | ||
|---|---|---|---|---|---|---|---|
true |
中等 |
1677 |
第 118 场双周赛 Q2 |
|
给你一个网格图,由 n + 2 条 横线段 和 m + 2 条 竖线段 组成,一开始所有区域均为 1 x 1 的单元格。
所有线段的编号从 1 开始。
给你两个整数 n 和 m 。
同时给你两个整数数组 hBars 和 vBars 。
hBars包含区间[2, n + 1]内 互不相同 的横线段编号。vBars包含[2, m + 1]内 互不相同的 竖线段编号。
如果满足以下条件之一,你可以 移除 两个数组中的部分线段:
- 如果移除的是横线段,它必须是
hBars中的值。 - 如果移除的是竖线段,它必须是
vBars中的值。
请你返回移除一些线段后(可能不移除任何线段),剩余网格图中 最大正方形 空洞的面积,正方形空洞的意思是正方形 内部 不含有任何线段。
示例 1:
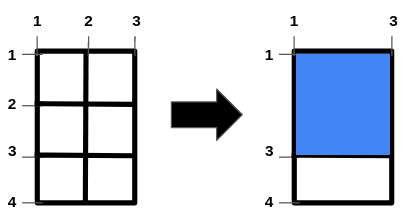
输入:n = 2, m = 1, hBars = [2,3], vBars = [2] 输出:4 解释:左边的图是一开始的网格图。 横线编号的范围是区间 [1,4] ,竖线编号的范围是区间 [1,3] 。 可以移除的横线段为 [2,3] ,竖线段为 [2] 。 一种得到最大正方形面积的方法是移除横线段 2 和竖线段 2 。 操作后得到的网格图如右图所示。 正方形空洞面积为 4。 无法得到面积大于 4 的正方形空洞。 所以答案为 4 。
示例 2:
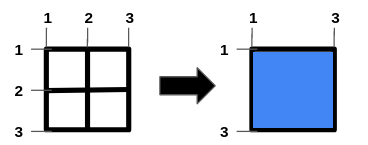
输入:n = 1, m = 1, hBars = [2], vBars = [2] 输出:4 解释:左边的图是一开始的网格图。 横线编号的范围是区间 [1,3] ,竖线编号的范围是区间 [1,3] 。 可以移除的横线段为 [2] ,竖线段为 [2] 。 一种得到最大正方形面积的方法是移除横线段 2 和竖线段 2 。 操作后得到的网格图如右图所示。 正方形空洞面积为 4。 无法得到面积大于 4 的正方形空洞。 所以答案为 4 。
示例 3:
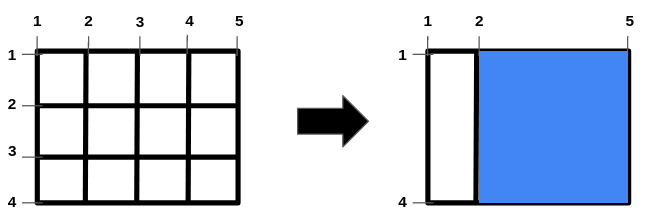
输入:n = 2, m = 3, hBars = [2,3], vBars = [2,3,4] 输出:9 解释:左边的图是一开始的网格图。 横线编号的范围是区间 [1,4] ,竖线编号的范围是区间 [1,5] 。 可以移除的横线段为 [2,3] ,竖线段为 [2,3,4] 。 一种得到最大正方形面积的方法是移除横线段 2、3 和竖线段 3、4 。 操作后得到的网格图如右图所示。 正方形空洞面积为 9。 无法得到面积大于 9 的正方形空洞。 所以答案为 9 。
提示:
1 <= n <= 1091 <= m <= 1091 <= hBars.length <= 1002 <= hBars[i] <= n + 11 <= vBars.length <= 1002 <= vBars[i] <= m + 1hBars中的值互不相同。vBars中的值互不相同。
题目实际上要我们找出数组中最长的连续递增子序列的长度,然后再加上
我们定义一个函数
对于数组
我们在求出
时间复杂度
class Solution:
def maximizeSquareHoleArea(
self, n: int, m: int, hBars: List[int], vBars: List[int]
) -> int:
def f(nums: List[int]) -> int:
nums.sort()
ans = cnt = 1
for i in range(1, len(nums)):
if nums[i] == nums[i - 1] + 1:
cnt += 1
ans = max(ans, cnt)
else:
cnt = 1
return ans + 1
return min(f(hBars), f(vBars)) ** 2class Solution {
public int maximizeSquareHoleArea(int n, int m, int[] hBars, int[] vBars) {
int x = Math.min(f(hBars), f(vBars));
return x * x;
}
private int f(int[] nums) {
Arrays.sort(nums);
int ans = 1, cnt = 1;
for (int i = 1; i < nums.length; ++i) {
if (nums[i] == nums[i - 1] + 1) {
ans = Math.max(ans, ++cnt);
} else {
cnt = 1;
}
}
return ans + 1;
}
}class Solution {
public:
int maximizeSquareHoleArea(int n, int m, vector<int>& hBars, vector<int>& vBars) {
auto f = [](vector<int>& nums) {
int ans = 1, cnt = 1;
sort(nums.begin(), nums.end());
for (int i = 1; i < nums.size(); ++i) {
if (nums[i] == nums[i - 1] + 1) {
ans = max(ans, ++cnt);
} else {
cnt = 1;
}
}
return ans + 1;
};
int x = min(f(hBars), f(vBars));
return x * x;
}
};func maximizeSquareHoleArea(n int, m int, hBars []int, vBars []int) int {
f := func(nums []int) int {
sort.Ints(nums)
ans, cnt := 1, 1
for i, x := range nums[1:] {
if x == nums[i]+1 {
cnt++
ans = max(ans, cnt)
} else {
cnt = 1
}
}
return ans + 1
}
x := min(f(hBars), f(vBars))
return x * x
}function maximizeSquareHoleArea(n: number, m: number, hBars: number[], vBars: number[]): number {
const f = (nums: number[]): number => {
nums.sort((a, b) => a - b);
let [ans, cnt] = [1, 1];
for (let i = 1; i < nums.length; ++i) {
if (nums[i] === nums[i - 1] + 1) {
ans = Math.max(ans, ++cnt);
} else {
cnt = 1;
}
}
return ans + 1;
};
return Math.min(f(hBars), f(vBars)) ** 2;
}impl Solution {
pub fn maximize_square_hole_area(n: i32, m: i32, h_bars: Vec<i32>, v_bars: Vec<i32>) -> i32 {
let f = |nums: &mut Vec<i32>| -> i32 {
let mut ans = 1;
let mut cnt = 1;
nums.sort();
for i in 1..nums.len() {
if nums[i] == nums[i - 1] + 1 {
cnt += 1;
ans = ans.max(cnt);
} else {
cnt = 1;
}
}
ans + 1
};
let mut h_bars = h_bars;
let mut v_bars = v_bars;
let x = f(&mut h_bars).min(f(&mut v_bars));
x * x
}
}