| comments | difficulty | edit_url | rating | source | tags | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
true |
困难 |
2581 |
第 340 场周赛 Q4 |
|
给你一个下标从 0 开始的 m x n 整数矩阵 grid 。你一开始的位置在 左上角 格子 (0, 0) 。
当你在格子 (i, j) 的时候,你可以移动到以下格子之一:
- 满足
j < k <= grid[i][j] + j的格子(i, k)(向右移动),或者 - 满足
i < k <= grid[i][j] + i的格子(k, j)(向下移动)。
请你返回到达 右下角 格子 (m - 1, n - 1) 需要经过的最少移动格子数,如果无法到达右下角格子,请你返回 -1 。
示例 1:
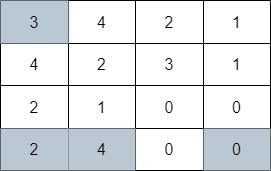
输入:grid = [[3,4,2,1],[4,2,3,1],[2,1,0,0],[2,4,0,0]] 输出:4 解释:上图展示了到达右下角格子经过的 4 个格子。
示例 2:
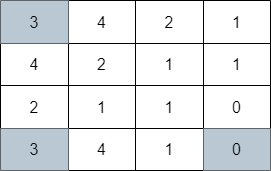
输入:grid = [[3,4,2,1],[4,2,1,1],[2,1,1,0],[3,4,1,0]] 输出:3 解释:上图展示了到达右下角格子经过的 3 个格子。
示例 3:
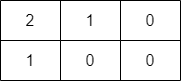
输入:grid = [[2,1,0],[1,0,0]] 输出:-1 解释:无法到达右下角格子。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 1051 <= m * n <= 1050 <= grid[i][j] < m * ngrid[m - 1][n - 1] == 0
我们记网格的行数为
对于每个格子
因此,我们可以对每一列
同理,我们可以对每一行
最终,我们可以得到从坐标
时间复杂度
class Solution:
def minimumVisitedCells(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
dist = [[-1] * n for _ in range(m)]
dist[0][0] = 1
row = [[] for _ in range(m)]
col = [[] for _ in range(n)]
for i in range(m):
for j in range(n):
while row[i] and grid[i][row[i][0][1]] + row[i][0][1] < j:
heappop(row[i])
if row[i] and (dist[i][j] == -1 or dist[i][j] > row[i][0][0] + 1):
dist[i][j] = row[i][0][0] + 1
while col[j] and grid[col[j][0][1]][j] + col[j][0][1] < i:
heappop(col[j])
if col[j] and (dist[i][j] == -1 or dist[i][j] > col[j][0][0] + 1):
dist[i][j] = col[j][0][0] + 1
if dist[i][j] != -1:
heappush(row[i], (dist[i][j], j))
heappush(col[j], (dist[i][j], i))
return dist[-1][-1]class Solution {
public int minimumVisitedCells(int[][] grid) {
int m = grid.length, n = grid[0].length;
int[][] dist = new int[m][n];
PriorityQueue<int[]>[] row = new PriorityQueue[m];
PriorityQueue<int[]>[] col = new PriorityQueue[n];
for (int i = 0; i < m; ++i) {
Arrays.fill(dist[i], -1);
row[i] = new PriorityQueue<>((a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);
}
for (int i = 0; i < n; ++i) {
col[i] = new PriorityQueue<>((a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);
}
dist[0][0] = 1;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
while (!row[i].isEmpty() && grid[i][row[i].peek()[1]] + row[i].peek()[1] < j) {
row[i].poll();
}
if (!row[i].isEmpty() && (dist[i][j] == -1 || row[i].peek()[0] + 1 < dist[i][j])) {
dist[i][j] = row[i].peek()[0] + 1;
}
while (!col[j].isEmpty() && grid[col[j].peek()[1]][j] + col[j].peek()[1] < i) {
col[j].poll();
}
if (!col[j].isEmpty() && (dist[i][j] == -1 || col[j].peek()[0] + 1 < dist[i][j])) {
dist[i][j] = col[j].peek()[0] + 1;
}
if (dist[i][j] != -1) {
row[i].offer(new int[] {dist[i][j], j});
col[j].offer(new int[] {dist[i][j], i});
}
}
}
return dist[m - 1][n - 1];
}
}class Solution {
public:
int minimumVisitedCells(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<vector<int>> dist(m, vector<int>(n, -1));
using pii = pair<int, int>;
priority_queue<pii, vector<pii>, greater<pii>> row[m];
priority_queue<pii, vector<pii>, greater<pii>> col[n];
dist[0][0] = 1;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
while (!row[i].empty() && grid[i][row[i].top().second] + row[i].top().second < j) {
row[i].pop();
}
if (!row[i].empty() && (dist[i][j] == -1 || row[i].top().first + 1 < dist[i][j])) {
dist[i][j] = row[i].top().first + 1;
}
while (!col[j].empty() && grid[col[j].top().second][j] + col[j].top().second < i) {
col[j].pop();
}
if (!col[j].empty() && (dist[i][j] == -1 || col[j].top().first + 1 < dist[i][j])) {
dist[i][j] = col[j].top().first + 1;
}
if (dist[i][j] != -1) {
row[i].emplace(dist[i][j], j);
col[j].emplace(dist[i][j], i);
}
}
}
return dist[m - 1][n - 1];
}
};func minimumVisitedCells(grid [][]int) int {
m, n := len(grid), len(grid[0])
dist := make([][]int, m)
row := make([]hp, m)
col := make([]hp, n)
for i := range dist {
dist[i] = make([]int, n)
for j := range dist[i] {
dist[i][j] = -1
}
}
dist[0][0] = 1
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
for len(row[i]) > 0 && grid[i][row[i][0].second]+row[i][0].second < j {
heap.Pop(&row[i])
}
if len(row[i]) > 0 && (dist[i][j] == -1 || row[i][0].first+1 < dist[i][j]) {
dist[i][j] = row[i][0].first + 1
}
for len(col[j]) > 0 && grid[col[j][0].second][j]+col[j][0].second < i {
heap.Pop(&col[j])
}
if len(col[j]) > 0 && (dist[i][j] == -1 || col[j][0].first+1 < dist[i][j]) {
dist[i][j] = col[j][0].first + 1
}
if dist[i][j] != -1 {
heap.Push(&row[i], pair{dist[i][j], j})
heap.Push(&col[j], pair{dist[i][j], i})
}
}
}
return dist[m-1][n-1]
}
type pair struct {
first int
second int
}
type hp []pair
func (a hp) Len() int { return len(a) }
func (a hp) Swap(i, j int) { a[i], a[j] = a[j], a[i] }
func (a hp) Less(i, j int) bool {
return a[i].first < a[j].first || (a[i].first == a[j].first && a[i].second < a[j].second)
}
func (a *hp) Push(x any) { *a = append(*a, x.(pair)) }
func (a *hp) Pop() any { l := len(*a); t := (*a)[l-1]; *a = (*a)[:l-1]; return t }