| comments | difficulty | edit_url | rating | source | tags | |||||
|---|---|---|---|---|---|---|---|---|---|---|
true |
困难 |
2228 |
第 99 场双周赛 Q4 |
|
Alice 有一棵 n 个节点的树,节点编号为 0 到 n - 1 。树用一个长度为 n - 1 的二维整数数组 edges 表示,其中 edges[i] = [ai, bi] ,表示树中节点 ai 和 bi 之间有一条边。
Alice 想要 Bob 找到这棵树的根。她允许 Bob 对这棵树进行若干次 猜测 。每一次猜测,Bob 做如下事情:
- 选择两个 不相等 的整数
u和v,且树中必须存在边[u, v]。 - Bob 猜测树中
u是v的 父节点 。
Bob 的猜测用二维整数数组 guesses 表示,其中 guesses[j] = [uj, vj] 表示 Bob 猜 uj 是 vj 的父节点。
Alice 非常懒,她不想逐个回答 Bob 的猜测,只告诉 Bob 这些猜测里面 至少 有 k 个猜测的结果为 true 。
给你二维整数数组 edges ,Bob 的所有猜测和整数 k ,请你返回可能成为树根的 节点数目 。如果没有这样的树,则返回 0。
示例 1:
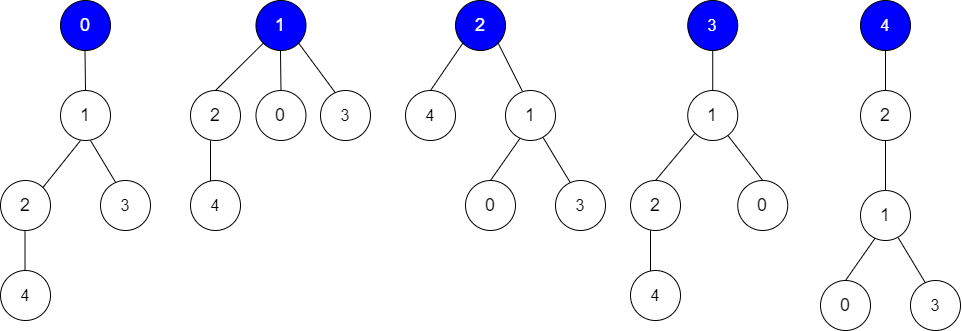
输入:edges = [[0,1],[1,2],[1,3],[4,2]], guesses = [[1,3],[0,1],[1,0],[2,4]], k = 3 输出:3 解释: 根为节点 0 ,正确的猜测为 [1,3], [0,1], [2,4] 根为节点 1 ,正确的猜测为 [1,3], [1,0], [2,4] 根为节点 2 ,正确的猜测为 [1,3], [1,0], [2,4] 根为节点 3 ,正确的猜测为 [1,0], [2,4] 根为节点 4 ,正确的猜测为 [1,3], [1,0] 节点 0 ,1 或 2 为根时,可以得到 3 个正确的猜测。
示例 2:
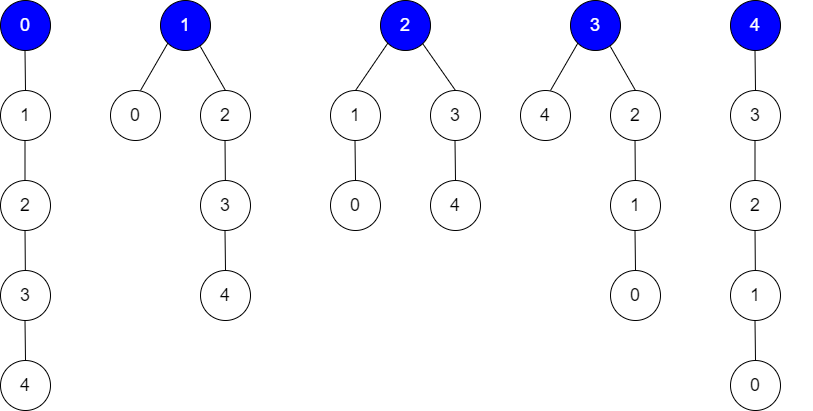
输入:edges = [[0,1],[1,2],[2,3],[3,4]], guesses = [[1,0],[3,4],[2,1],[3,2]], k = 1 输出:5 解释: 根为节点 0 ,正确的猜测为 [3,4] 根为节点 1 ,正确的猜测为 [1,0], [3,4] 根为节点 2 ,正确的猜测为 [1,0], [2,1], [3,4] 根为节点 3 ,正确的猜测为 [1,0], [2,1], [3,2], [3,4] 根为节点 4 ,正确的猜测为 [1,0], [2,1], [3,2] 任何节点为根,都至少有 1 个正确的猜测。
提示:
edges.length == n - 12 <= n <= 1051 <= guesses.length <= 1050 <= ai, bi, uj, vj <= n - 1ai != biuj != vjedges表示一棵有效的树。guesses[j]是树中的一条边。guesses是唯一的。0 <= k <= guesses.length
我们先遍历题目给定的边集合
接下来,我们先从节点
然后,我们再从节点
因此,问题就转化为了求以每个点为根的树中,有多少条边在
假设我们当前遍历到节点
时间复杂度
相似题目:
class Solution:
def rootCount(
self, edges: List[List[int]], guesses: List[List[int]], k: int
) -> int:
def dfs1(i, fa):
nonlocal cnt
for j in g[i]:
if j != fa:
cnt += gs[(i, j)]
dfs1(j, i)
def dfs2(i, fa):
nonlocal ans, cnt
ans += cnt >= k
for j in g[i]:
if j != fa:
cnt -= gs[(i, j)]
cnt += gs[(j, i)]
dfs2(j, i)
cnt -= gs[(j, i)]
cnt += gs[(i, j)]
g = defaultdict(list)
for a, b in edges:
g[a].append(b)
g[b].append(a)
gs = Counter((u, v) for u, v in guesses)
cnt = 0
dfs1(0, -1)
ans = 0
dfs2(0, -1)
return ansclass Solution {
private List<Integer>[] g;
private Map<Long, Integer> gs = new HashMap<>();
private int ans;
private int k;
private int cnt;
private int n;
public int rootCount(int[][] edges, int[][] guesses, int k) {
this.k = k;
n = edges.length + 1;
g = new List[n];
Arrays.setAll(g, e -> new ArrayList<>());
for (var e : edges) {
int a = e[0], b = e[1];
g[a].add(b);
g[b].add(a);
}
for (var e : guesses) {
int a = e[0], b = e[1];
gs.merge(f(a, b), 1, Integer::sum);
}
dfs1(0, -1);
dfs2(0, -1);
return ans;
}
private void dfs1(int i, int fa) {
for (int j : g[i]) {
if (j != fa) {
cnt += gs.getOrDefault(f(i, j), 0);
dfs1(j, i);
}
}
}
private void dfs2(int i, int fa) {
ans += cnt >= k ? 1 : 0;
for (int j : g[i]) {
if (j != fa) {
int a = gs.getOrDefault(f(i, j), 0);
int b = gs.getOrDefault(f(j, i), 0);
cnt -= a;
cnt += b;
dfs2(j, i);
cnt -= b;
cnt += a;
}
}
}
private long f(int i, int j) {
return 1L * i * n + j;
}
}class Solution {
public:
int rootCount(vector<vector<int>>& edges, vector<vector<int>>& guesses, int k) {
int n = edges.size() + 1;
vector<int> g[n];
unordered_map<long long, int> gs;
auto f = [&](int i, int j) {
return 1LL * i * n + j;
};
for (auto& e : edges) {
int a = e[0], b = e[1];
g[a].push_back(b);
g[b].push_back(a);
}
for (auto& e : guesses) {
int a = e[0], b = e[1];
gs[f(a, b)]++;
}
int ans = 0;
int cnt = 0;
function<void(int, int)> dfs1 = [&](int i, int fa) {
for (int& j : g[i]) {
if (j != fa) {
cnt += gs[f(i, j)];
dfs1(j, i);
}
}
};
function<void(int, int)> dfs2 = [&](int i, int fa) {
ans += cnt >= k;
for (int& j : g[i]) {
if (j != fa) {
int a = gs[f(i, j)];
int b = gs[f(j, i)];
cnt -= a;
cnt += b;
dfs2(j, i);
cnt -= b;
cnt += a;
}
}
};
dfs1(0, -1);
dfs2(0, -1);
return ans;
}
};func rootCount(edges [][]int, guesses [][]int, k int) (ans int) {
n := len(edges) + 1
g := make([][]int, n)
gs := map[int]int{}
for _, e := range edges {
a, b := e[0], e[1]
g[a] = append(g[a], b)
g[b] = append(g[b], a)
}
f := func(i, j int) int {
return i*n + j
}
for _, e := range guesses {
a, b := e[0], e[1]
gs[f(a, b)]++
}
cnt := 0
var dfs1 func(i, fa int)
var dfs2 func(i, fa int)
dfs1 = func(i, fa int) {
for _, j := range g[i] {
if j != fa {
cnt += gs[f(i, j)]
dfs1(j, i)
}
}
}
dfs2 = func(i, fa int) {
if cnt >= k {
ans++
}
for _, j := range g[i] {
if j != fa {
a, b := gs[f(i, j)], gs[f(j, i)]
cnt -= a
cnt += b
dfs2(j, i)
cnt -= b
cnt += a
}
}
}
dfs1(0, -1)
dfs2(0, -1)
return
}function rootCount(edges: number[][], guesses: number[][], k: number): number {
const n = edges.length + 1;
const g: number[][] = Array.from({ length: n }, () => []);
const gs: Map<number, number> = new Map();
const f = (i: number, j: number) => i * n + j;
for (const [a, b] of edges) {
g[a].push(b);
g[b].push(a);
}
for (const [a, b] of guesses) {
const x = f(a, b);
gs.set(x, gs.has(x) ? gs.get(x)! + 1 : 1);
}
let ans = 0;
let cnt = 0;
const dfs1 = (i: number, fa: number): void => {
for (const j of g[i]) {
if (j !== fa) {
cnt += gs.get(f(i, j)) || 0;
dfs1(j, i);
}
}
};
const dfs2 = (i: number, fa: number): void => {
ans += cnt >= k ? 1 : 0;
for (const j of g[i]) {
if (j !== fa) {
const a = gs.get(f(i, j)) || 0;
const b = gs.get(f(j, i)) || 0;
cnt -= a;
cnt += b;
dfs2(j, i);
cnt -= b;
cnt += a;
}
}
};
dfs1(0, -1);
dfs2(0, -1);
return ans;
}