| comments | difficulty | edit_url | rating | source | tags | |||||
|---|---|---|---|---|---|---|---|---|---|---|
true |
中等 |
1682 |
第 93 场双周赛 Q2 |
|
给你一个 n 个点的无向图,节点从 0 到 n - 1 编号。给你一个长度为 n 下标从 0 开始的整数数组 vals ,其中 vals[i] 表示第 i 个节点的值。
同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条双向边。
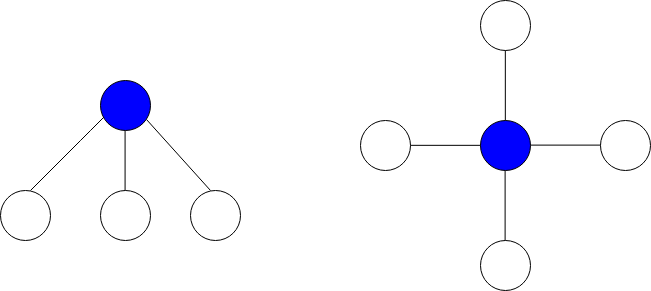
星图 是给定图中的一个子图,它包含一个中心节点和 0 个或更多个邻居。换言之,星图是给定图中一个边的子集,且这些边都有一个公共节点。
下图分别展示了有 3 个和 4 个邻居的星图,蓝色节点为中心节点。
星和 定义为星图中所有节点值的和。
给你一个整数 k ,请你返回 至多 包含 k 条边的星图中的 最大星和 。
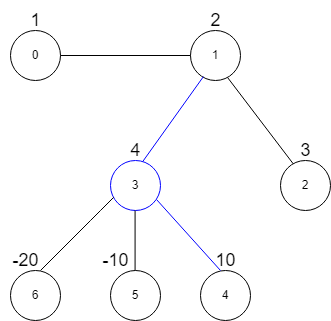
示例 1:
输入:vals = [1,2,3,4,10,-10,-20], edges = [[0,1],[1,2],[1,3],[3,4],[3,5],[3,6]], k = 2 输出:16 解释:上图展示了输入示例。 最大星和对应的星图在上图中用蓝色标出。中心节点是 3 ,星图中还包含邻居 1 和 4 。 无法得到一个和大于 16 且边数不超过 2 的星图。
示例 2:
输入:vals = [-5], edges = [], k = 0 输出:-5 解释:只有一个星图,就是节点 0 自己。 所以我们返回 -5 。
提示:
n == vals.length1 <= n <= 105-104 <= vals[i] <= 1040 <= edges.length <= min(n * (n - 1) / 2, 105)edges[i].length == 20 <= ai, bi <= n - 1ai != bi0 <= k <= n - 1
我们先将输入的边集合转换成邻接表,其中
然后我们遍历每个节点
最后返回最大星和即可。
时间复杂度
class Solution:
def maxStarSum(self, vals: List[int], edges: List[List[int]], k: int) -> int:
g = defaultdict(list)
for a, b in edges:
if vals[b] > 0:
g[a].append(vals[b])
if vals[a] > 0:
g[b].append(vals[a])
for bs in g.values():
bs.sort(reverse=True)
return max(v + sum(g[i][:k]) for i, v in enumerate(vals))class Solution {
public int maxStarSum(int[] vals, int[][] edges, int k) {
int n = vals.length;
List<Integer>[] g = new List[n];
Arrays.setAll(g, key -> new ArrayList<>());
for (var e : edges) {
int a = e[0], b = e[1];
if (vals[b] > 0) {
g[a].add(vals[b]);
}
if (vals[a] > 0) {
g[b].add(vals[a]);
}
}
for (var e : g) {
Collections.sort(e, (a, b) -> b - a);
}
int ans = Integer.MIN_VALUE;
for (int i = 0; i < n; ++i) {
int v = vals[i];
for (int j = 0; j < Math.min(g[i].size(), k); ++j) {
v += g[i].get(j);
}
ans = Math.max(ans, v);
}
return ans;
}
}class Solution {
public:
int maxStarSum(vector<int>& vals, vector<vector<int>>& edges, int k) {
int n = vals.size();
vector<vector<int>> g(n);
for (auto& e : edges) {
int a = e[0], b = e[1];
if (vals[b] > 0) g[a].emplace_back(vals[b]);
if (vals[a] > 0) g[b].emplace_back(vals[a]);
}
for (auto& e : g) sort(e.rbegin(), e.rend());
int ans = INT_MIN;
for (int i = 0; i < n; ++i) {
int v = vals[i];
for (int j = 0; j < min((int) g[i].size(), k); ++j) v += g[i][j];
ans = max(ans, v);
}
return ans;
}
};func maxStarSum(vals []int, edges [][]int, k int) (ans int) {
n := len(vals)
g := make([][]int, n)
for _, e := range edges {
a, b := e[0], e[1]
if vals[b] > 0 {
g[a] = append(g[a], vals[b])
}
if vals[a] > 0 {
g[b] = append(g[b], vals[a])
}
}
for _, e := range g {
sort.Sort(sort.Reverse(sort.IntSlice(e)))
}
ans = math.MinInt32
for i, v := range vals {
for j := 0; j < min(len(g[i]), k); j++ {
v += g[i][j]
}
ans = max(ans, v)
}
return
}