| comments | difficulty | edit_url | tags | |||
|---|---|---|---|---|---|---|
true |
中等 |
|
给定一个 加权 树,由 n 个节点组成,从 0 到 n - 1。
该树以节点 0 为 根,用大小为 n 的二维数组 edges 表示,其中 edges[i] = [pari, weighti] 表示节点 pari 是节点 i 的 父 节点,它们之间的边的权重等于 weighti。因为根结点 没有 父结点,所以有 edges[0] = [-1, -1]。
从树中选择一些边,使所选的两条边都不 相邻,所选边的权值之 和 最大。
返回所选边的 最大 和。
注意:
- 你可以 不选择 树中的任何边,在这种情况下权值和将为
0。 - 如果树中的两条边
Edge1和Edge2有一个 公共 节点,它们就是 相邻 的。- 换句话说,如果
Edge1连接节点a和b,Edge2连接节点b和c,它们是相邻的。
- 换句话说,如果
示例 1:
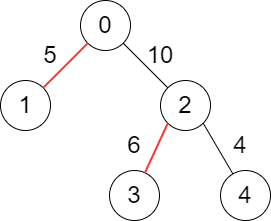
输入: edges = [[-1,-1],[0,5],[0,10],[2,6],[2,4]] 输出: 11 解释: 上面的图表显示了我们必须选择红色的边。 总分是 5 + 6 = 11. 可以看出,没有更好的分数可以获得。
示例 2:
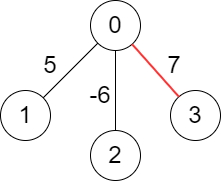
输入: edges = [[-1,-1],[0,5],[0,-6],[0,7]] 输出: 7 解释: 我们选择权值为 7 的边。 注意,我们不能选择一条以上的边,因为所有的边都是彼此相邻的。
提示:
n == edges.length1 <= n <= 105edges[i].length == 2par0 == weight0 == -1i >= 1时0 <= pari <= n - 1。pari != ii >= 1时-106 <= weighti <= 106。edges表示有效的树。
我们设计一个函数
我们可以发现,对于当前节点
- 如果
$i$ 与父节点的边被选择,则它与子节点的所有边都不能被选择,那么当前节点的$a$ 值就是其所有子节点的$b$ 值之和; - 如果
$i$ 与父节点的边没被选择,那么可以选择它与子节点的最多一条边,那么当前节点的$b$ 值就是其选中的子节点的$a$ 值与未选中的子节点的$b$ 值之和,再加上$i$ 与选中的子节点之间的边的权值。
我们调用
时间复杂度
class Solution:
def maxScore(self, edges: List[List[int]]) -> int:
def dfs(i):
a = b = t = 0
for j, w in g[i]:
x, y = dfs(j)
a += y
b += y
t = max(t, x - y + w)
b += t
return a, b
g = defaultdict(list)
for i, (p, w) in enumerate(edges[1:], 1):
g[p].append((i, w))
return dfs(0)[1]class Solution {
private List<int[]>[] g;
public long maxScore(int[][] edges) {
int n = edges.length;
g = new List[n];
Arrays.setAll(g, k -> new ArrayList<>());
for (int i = 1; i < n; ++i) {
int p = edges[i][0], w = edges[i][1];
g[p].add(new int[] {i, w});
}
return dfs(0)[1];
}
private long[] dfs(int i) {
long a = 0, b = 0, t = 0;
for (int[] nxt : g[i]) {
int j = nxt[0], w = nxt[1];
long[] s = dfs(j);
a += s[1];
b += s[1];
t = Math.max(t, s[0] - s[1] + w);
}
b += t;
return new long[] {a, b};
}
}class Solution {
public:
long long maxScore(vector<vector<int>>& edges) {
int n = edges.size();
vector<vector<pair<int, int>>> g(n);
for (int i = 1; i < n; ++i) {
int p = edges[i][0], w = edges[i][1];
g[p].emplace_back(i, w);
}
using ll = long long;
using pll = pair<ll, ll>;
function<pll(int)> dfs = [&](int i) -> pll {
ll a = 0, b = 0, t = 0;
for (auto& [j, w] : g[i]) {
auto [x, y] = dfs(j);
a += y;
b += y;
t = max(t, x - y + w);
}
b += t;
return make_pair(a, b);
};
return dfs(0).second;
}
};func maxScore(edges [][]int) int64 {
n := len(edges)
g := make([][][2]int, n)
for i := 1; i < n; i++ {
p, w := edges[i][0], edges[i][1]
g[p] = append(g[p], [2]int{i, w})
}
var dfs func(int) [2]int
dfs = func(i int) [2]int {
var a, b, t int
for _, e := range g[i] {
j, w := e[0], e[1]
s := dfs(j)
a += s[1]
b += s[1]
t = max(t, s[0]-s[1]+w)
}
b += t
return [2]int{a, b}
}
return int64(dfs(0)[1])
}