Skip to content

Latest commit

 

History

History
202 lines (161 loc) · 6.79 KB

README.md

File metadata and controls

202 lines (161 loc) · 6.79 KB
comments difficulty edit_url tags
true
中等
数组
前缀和

2237. 计算街道上满足所需亮度的位置数量 🔒

English Version

题目描述

给你一个整数 n。一条完全笔直的街道用一条从 0 到 n - 1 的数轴表示。给你一个二维整数数组 lights，表示街道上的路灯。每个 lights[i] = [positioni, rangei] 表示在位置 positioni 有一盏路灯，从 [max(0, positioni - rangei), min(n - 1, positioni + rangei)] (包含边界) 开始照亮该区域。

位置 p 的 亮度 定义为点亮位置 p 的路灯的数量。给定一个大小为 n 的整数数组 requirement，数组的 下标从 0 开始，其中 requirement[i] 是街道上第 i 个位置的最小 亮度。

返回街道上 0 到 n - 1 之间 亮度至少满足 requirement[i] 的位置 i 的数量。

 

示例 1:

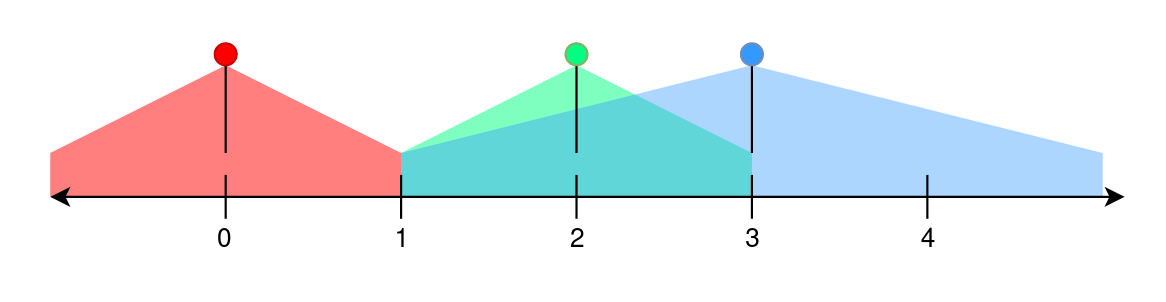
输入: n = 5, lights = [[0,1],[2,1],[3,2]], requirement = [0,2,1,4,1]
输出: 4
解释:
- 第一盏路灯照亮区域范围为 [max(0,0 - 1)， min(n - 1,0 + 1)] =[0,1](含边界)。
- 第二盏路灯的点亮范围为 [max(0,2 - 1)， min(n - 1,2 + 1)] =[1,3](含边界)。
- 第三盏路灯照亮区域范围为 [max(0,3 - 2)， min(n - 1,3 + 2)] =[1,4](含边界)。

    

  • 位置 0 被第一盏路灯覆盖。它被 1 个路灯覆盖，大于 requirement[0]。
    • 

  • 位置 1 被第一、第二和第三个路灯覆盖。被 3 个路灯覆盖，大于 requirement[1]。
    • 

  • 位置 2 由第二和第三路灯覆盖。被 2 个路灯覆盖，大于 requirement[2]。
    • 

  • 位置 3 由第二和第三路灯覆盖。它被 2 个路灯覆盖，比 requirement[3] 少。
    • 

  • 位置 4 被第三个路灯覆盖。它被 1 盏路灯覆盖，等于 requirement[4]。
    • 



位置 0、1、2、4 满足要求，因此返回4。

示例 2:

输入: n = 1, lights = [[0,1]], requirement = [2]
输出: 0
解释:
- 第一盏路灯照亮区域范围为 [max(0,0 - 1)， min(n - 1,0 + 1)] =[0,0](含边界)。
- 位置 0 被第一盏路灯覆盖。它被 1 个路灯覆盖，比 requirement[0] 少。
- 返回0，因为没有位置满足亮度要求。

 

提示:

  • 1 <= n <= 105
  • 1 <= lights.length <= 105
  • 0 <= positioni < n
  • 0 <= rangei <= 105
  • requirement.length == n
  • 0 <= requirement[i] <= 105

解法

方法一：差分数组

对一段连续的区间 $[i, j]$ 同时加上一个值 $v$，可以通过差分数组来实现。

我们定义一个长度为 $n + 1$ 的数组 $\textit{d}$，接下来对于每个路灯，我们计算出它的左边界 $i = \max(0, p - r)$ 和右边界 $j = \min(n - 1, p + r)$，然后将 $\textit{d}[i]$ 加上 $1$，将 $\textit{d}[j + 1]$ 减去 $1$。

然后，我们对 $\textit{d}$ 进行前缀和运算，对于每个位置 $i$，如果 $\textit{d}[i]$ 的前缀和大于等于 $\textit{requirement}[i]$，则说明该位置满足要求，将答案加一。

最后返回答案即可。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 为路灯数量。

Python3

class Solution:
    def meetRequirement(
        self, n: int, lights: List[List[int]], requirement: List[int]
    ) -> int:
        d = [0] * (n + 1)
        for p, r in lights:
            i, j = max(0, p - r), min(n - 1, p + r)
            d[i] += 1
            d[j + 1] -= 1
        return sum(s >= r for s, r in zip(accumulate(d), requirement))

Java

class Solution {
    public int meetRequirement(int n, int[][] lights, int[] requirement) {
        int[] d = new int[n + 1];
        for (int[] e : lights) {
            int i = Math.max(0, e[0] - e[1]);
            int j = Math.min(n - 1, e[0] + e[1]);
            ++d[i];
            --d[j + 1];
        }
        int s = 0;
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            s += d[i];
            if (s >= requirement[i]) {
                ++ans;
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int meetRequirement(int n, vector<vector<int>>& lights, vector<int>& requirement) {
        vector<int> d(n + 1);
        for (const auto& e : lights) {
            int i = max(0, e[0] - e[1]), j = min(n - 1, e[0] + e[1]);
            ++d[i];
            --d[j + 1];
        }
        int s = 0, ans = 0;
        for (int i = 0; i < n; ++i) {
            s += d[i];
            if (s >= requirement[i]) {
                ++ans;
            }
        }
        return ans;
    }
};

Go

func meetRequirement(n int, lights [][]int, requirement []int) (ans int) {
	d := make([]int, n+1)
	for _, e := range lights {
		i, j := max(0, e[0]-e[1]), min(n-1, e[0]+e[1])
		d[i]++
		d[j+1]--
	}
	s := 0
	for i, r := range requirement {
		s += d[i]
		if s >= r {
			ans++
		}
	}
	return
}

TypeScript

function meetRequirement(n: number, lights: number[][], requirement: number[]): number {
    const d: number[] = Array(n + 1).fill(0);
    for (const [p, r] of lights) {
        const [i, j] = [Math.max(0, p - r), Math.min(n - 1, p + r)];
        ++d[i];
        --d[j + 1];
    }
    let [ans, s] = [0, 0];
    for (let i = 0; i < n; ++i) {
        s += d[i];
        if (s >= requirement[i]) {
            ++ans;
        }
    }
    return ans;
}