| comments | difficulty | edit_url | rating | source | tags | |||
|---|---|---|---|---|---|---|---|---|
true |
中等 |
1779 |
第 186 场周赛 Q3 |
|
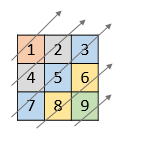
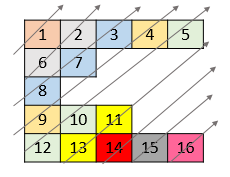
给你一个列表 nums ,里面每一个元素都是一个整数列表。请你依照下面各图的规则,按顺序返回 nums 中对角线上的整数。
示例 1:
输入:nums = [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,4,2,7,5,3,8,6,9]
示例 2:
输入:nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]] 输出:[1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16]
示例 3:
输入:nums = [[1,2,3],[4],[5,6,7],[8],[9,10,11]] 输出:[1,4,2,5,3,8,6,9,7,10,11]
示例 4:
输入:nums = [[1,2,3,4,5,6]] 输出:[1,2,3,4,5,6]
提示:
1 <= nums.length <= 10^51 <= nums[i].length <= 10^51 <= nums[i][j] <= 10^9nums中最多有10^5个数字。
我们观察到:
- 每一条对角线上的
$i + j$ 的值都是相同的; - 下一条对角线的
$i + j$ 的值比前一条对角线的大; - 在同一条对角线中的
$i + j$ 是相同的,而$j$ 值是从小到大递增。
因此,我们将所有数字以
时间复杂度
class Solution:
def findDiagonalOrder(self, nums: List[List[int]]) -> List[int]:
arr = []
for i, row in enumerate(nums):
for j, v in enumerate(row):
arr.append((i + j, j, v))
arr.sort()
return [v[2] for v in arr]class Solution {
public int[] findDiagonalOrder(List<List<Integer>> nums) {
List<int[]> arr = new ArrayList<>();
for (int i = 0; i < nums.size(); ++i) {
for (int j = 0; j < nums.get(i).size(); ++j) {
arr.add(new int[] {i + j, j, nums.get(i).get(j)});
}
}
arr.sort((a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);
int[] ans = new int[arr.size()];
for (int i = 0; i < arr.size(); ++i) {
ans[i] = arr.get(i)[2];
}
return ans;
}
}class Solution {
public:
vector<int> findDiagonalOrder(vector<vector<int>>& nums) {
vector<tuple<int, int, int>> arr;
for (int i = 0; i < nums.size(); ++i) {
for (int j = 0; j < nums[i].size(); ++j) {
arr.push_back({i + j, j, nums[i][j]});
}
}
sort(arr.begin(), arr.end());
vector<int> ans;
for (auto& e : arr) {
ans.push_back(get<2>(e));
}
return ans;
}
};func findDiagonalOrder(nums [][]int) []int {
arr := [][]int{}
for i, row := range nums {
for j, v := range row {
arr = append(arr, []int{i + j, j, v})
}
}
sort.Slice(arr, func(i, j int) bool {
if arr[i][0] == arr[j][0] {
return arr[i][1] < arr[j][1]
}
return arr[i][0] < arr[j][0]
})
ans := []int{}
for _, v := range arr {
ans = append(ans, v[2])
}
return ans
}function findDiagonalOrder(nums: number[][]): number[] {
const arr: number[][] = [];
for (let i = 0; i < nums.length; ++i) {
for (let j = 0; j < nums[i].length; ++j) {
arr.push([i + j, j, nums[i][j]]);
}
}
arr.sort((a, b) => (a[0] === b[0] ? a[1] - b[1] : a[0] - b[0]));
return arr.map(x => x[2]);
}public class Solution {
public int[] FindDiagonalOrder(IList<IList<int>> nums) {
List<int[]> arr = new List<int[]>();
for (int i = 0; i < nums.Count; ++i) {
for (int j = 0; j < nums[i].Count; ++j) {
arr.Add(new int[] { i + j, j, nums[i][j] });
}
}
arr.Sort((a, b) => a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);
int[] ans = new int[arr.Count];
for (int i = 0; i < arr.Count; ++i) {
ans[i] = arr[i][2];
}
return ans;
}
}