| comments | difficulty | edit_url | rating | source | tags | ||||
|---|---|---|---|---|---|---|---|---|---|
true |
中等 |
1387 |
第 16 场双周赛 Q3 |
|
给你一棵二叉树的根节点 root ,请你返回 层数最深的叶子节点的和 。
示例 1:
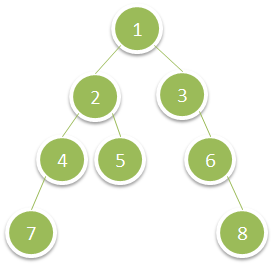
输入:root = [1,2,3,4,5,null,6,7,null,null,null,null,8] 输出:15
示例 2:
输入:root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5] 输出:19
提示:
- 树中节点数目在范围
[1, 104]之间。 1 <= Node.val <= 100
我们可以使用广度优先搜索,逐层遍历二叉树,并在遍历到每一层时计算该层的节点值之和。遍历完成后,返回最后一层的节点值之和。
时间复杂度
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def deepestLeavesSum(self, root: Optional[TreeNode]) -> int:
q = deque([root])
while q:
ans = 0
for _ in range(len(q)):
node = q.popleft()
ans += node.val
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
return ans/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int deepestLeavesSum(TreeNode root) {
Deque<TreeNode> q = new ArrayDeque<>();
q.offer(root);
int ans = 0;
while (!q.isEmpty()) {
ans = 0;
for (int k = q.size(); k > 0; --k) {
TreeNode node = q.poll();
ans += node.val;
if (node.left != null) {
q.offer(node.left);
}
if (node.right != null) {
q.offer(node.right);
}
}
}
return ans;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int deepestLeavesSum(TreeNode* root) {
int ans = 0;
queue<TreeNode*> q{{root}};
while (!q.empty()) {
ans = 0;
for (int k = q.size(); k; --k) {
TreeNode* node = q.front();
q.pop();
ans += node->val;
if (node->left) {
q.push(node->left);
}
if (node->right) {
q.push(node->right);
}
}
}
return ans;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func deepestLeavesSum(root *TreeNode) (ans int) {
q := []*TreeNode{root}
for len(q) > 0 {
ans = 0
for k := len(q); k > 0; k-- {
node := q[0]
q = q[1:]
ans += node.Val
if node.Left != nil {
q = append(q, node.Left)
}
if node.Right != nil {
q = append(q, node.Right)
}
}
}
return
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function deepestLeavesSum(root: TreeNode | null): number {
let q: TreeNode[] = [root];
let ans = 0;
while (q.length) {
const nq: TreeNode[] = [];
ans = 0;
for (const { val, left, right } of q) {
ans += val;
left && nq.push(left);
right && nq.push(right);
}
q = nq;
}
return ans;
}// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
use std::rc::Rc;
use std::cell::RefCell;
use std::collections::VecDeque;
impl Solution {
pub fn deepest_leaves_sum(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
let mut q = VecDeque::new();
q.push_back(root);
let mut ans = 0;
while !q.is_empty() {
ans = 0;
for _ in 0..q.len() {
if let Some(Some(node)) = q.pop_front() {
let node = node.borrow();
ans += node.val;
if node.left.is_some() {
q.push_back(node.left.clone());
}
if node.right.is_some() {
q.push_back(node.right.clone());
}
}
}
}
ans
}
}我们可以使用深度优先搜索,递归遍历二叉树,并在遍历的过程中记录当前节点的深度,以及最大深度和最深叶子节点的和。遍历到当前节点时,如果当前节点的深度等于最大深度,则将当前节点的值加到最深叶子节点的和中;如果当前节点的深度大于最大深度,则将最大深度更新为当前节点的深度,并将最深叶子节点的和更新为当前节点的值。
时间复杂度
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def deepestLeavesSum(self, root: Optional[TreeNode]) -> int:
def dfs(root, i):
nonlocal ans, mx
if root is None:
return
if i == mx:
ans += root.val
elif i > mx:
ans = root.val
mx = i
dfs(root.left, i + 1)
dfs(root.right, i + 1)
ans = mx = 0
dfs(root, 1)
return ans/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
int mx;
int ans;
public int deepestLeavesSum(TreeNode root) {
dfs(root, 1);
return ans;
}
private void dfs(TreeNode root, int i) {
if (root == null) {
return;
}
if (i > mx) {
mx = i;
ans = root.val;
} else if (i == mx) {
ans += root.val;
}
dfs(root.left, i + 1);
dfs(root.right, i + 1);
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int deepestLeavesSum(TreeNode* root) {
int mx = 0, ans = 0;
auto dfs = [&](this auto&& dfs, TreeNode* root, int i) {
if (!root) {
return;
}
if (i == mx) {
ans += root->val;
} else if (i > mx) {
mx = i;
ans = root->val;
}
dfs(root->left, i + 1);
dfs(root->right, i + 1);
};
dfs(root, 1);
return ans;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func deepestLeavesSum(root *TreeNode) int {
ans, mx := 0, 0
var dfs func(*TreeNode, int)
dfs = func(root *TreeNode, i int) {
if root == nil {
return
}
if i == mx {
ans += root.Val
} else if i > mx {
mx = i
ans = root.Val
}
dfs(root.Left, i+1)
dfs(root.Right, i+1)
}
dfs(root, 1)
return ans
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function deepestLeavesSum(root: TreeNode | null): number {
let [ans, mx] = [0, 0];
const dfs = (root: TreeNode | null, i: number) => {
if (!root) {
return;
}
if (i > mx) {
mx = i;
ans = root.val;
} else if (i === mx) {
ans += root.val;
}
dfs(root.left, i + 1);
dfs(root.right, i + 1);
};
dfs(root, 1);
return ans;
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
void dfs(struct TreeNode* root, int depth, int* maxDepth, int* res) {
if (!root->left && !root->right) {
if (depth == *maxDepth) {
*res += root->val;
} else if (depth > *maxDepth) {
*maxDepth = depth;
*res = root->val;
}
return;
}
if (root->left) {
dfs(root->left, depth + 1, maxDepth, res);
}
if (root->right) {
dfs(root->right, depth + 1, maxDepth, res);
}
}
int deepestLeavesSum(struct TreeNode* root) {
int res = 0;
int maxDepth = 0;
dfs(root, 0, &maxDepth, &res);
return res;
}