| comments | difficulty | edit_url | rating | source | tags | ||||
|---|---|---|---|---|---|---|---|---|---|
true |
困难 |
1797 |
第 132 场周赛 Q4 |
|
我们从二叉树的根节点 root 开始进行深度优先搜索。
在遍历中的每个节点处,我们输出 D 条短划线(其中 D 是该节点的深度),然后输出该节点的值。(如果节点的深度为 D,则其直接子节点的深度为 D + 1。根节点的深度为 0)。
如果节点只有一个子节点,那么保证该子节点为左子节点。
给出遍历输出 S,还原树并返回其根节点 root。
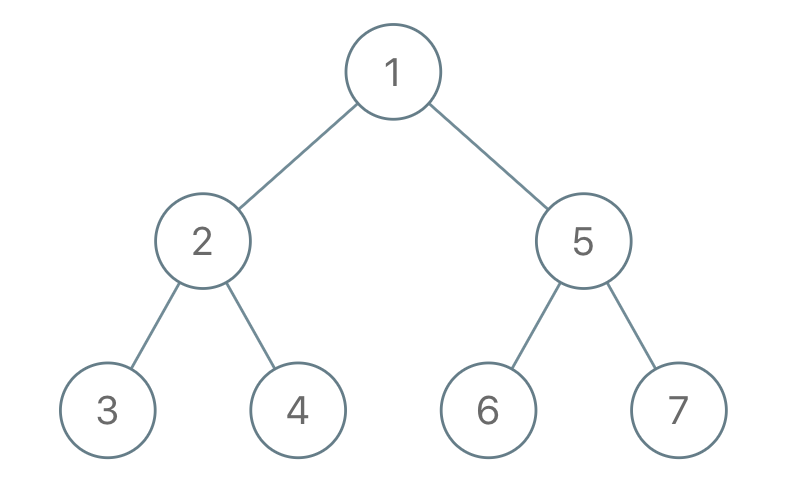
示例 1:
输入:"1-2--3--4-5--6--7" 输出:[1,2,5,3,4,6,7]
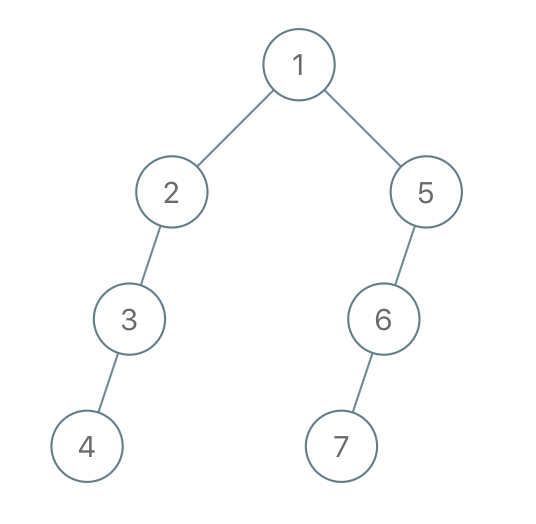
示例 2:
输入:"1-2--3---4-5--6---7" 输出:[1,2,5,3,null,6,null,4,null,7]
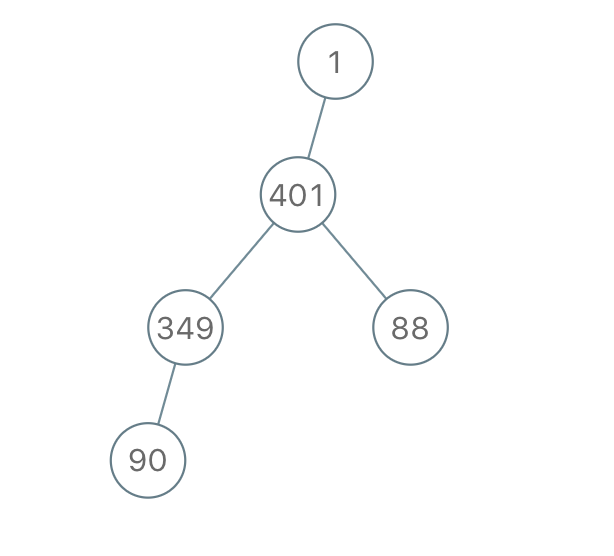
示例 3:
输入:"1-401--349---90--88" 输出:[1,401,null,349,88,90]
提示:
- 原始树中的节点数介于
1和1000之间。 - 每个节点的值介于
1和10 ^ 9之间。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* recoverFromPreorder(string S) {
stack<TreeNode*> st;
int depth = 0;
int num = 0;
for (int i = 0; i < S.length(); ++i) {
if (S[i] == '-') {
depth++;
} else {
num = 10 * num + S[i] - '0';
}
if (i + 1 >= S.length() || (isdigit(S[i]) && S[i + 1] == '-')) {
TreeNode* newNode = new TreeNode(num);
while (st.size() > depth) {
st.pop();
}
if (!st.empty()) {
if (st.top()->left == nullptr) {
st.top()->left = newNode;
} else {
st.top()->right = newNode;
}
}
st.push(newNode);
depth = 0;
num = 0;
}
}
TreeNode* res;
while (!st.empty()) {
res = st.top();
st.pop();
}
return res;
}
};