| comments | difficulty | edit_url | tags | |||
|---|---|---|---|---|---|---|
true |
中等 |
|
给定在 xy 平面上的一组点,确定由这些点组成的任何矩形的最小面积,其中矩形的边不一定平行于 x 轴和 y 轴。
如果没有任何矩形,就返回 0。
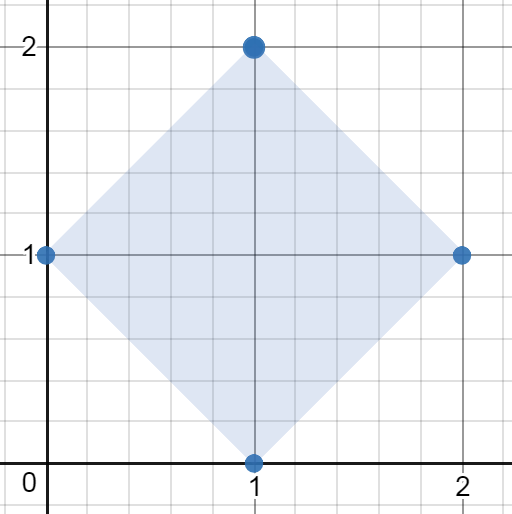
示例 1:
输入:[[1,2],[2,1],[1,0],[0,1]] 输出:2.00000 解释:最小面积的矩形出现在 [1,2],[2,1],[1,0],[0,1] 处,面积为 2。
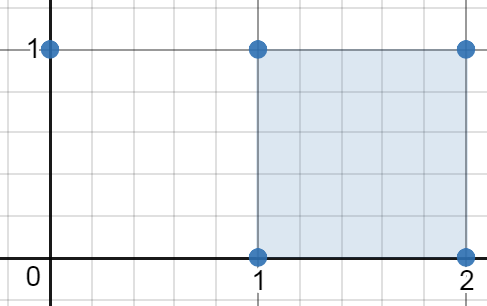
示例 2:
输入:[[0,1],[2,1],[1,1],[1,0],[2,0]] 输出:1.00000 解释:最小面积的矩形出现在 [1,0],[1,1],[2,1],[2,0] 处,面积为 1。
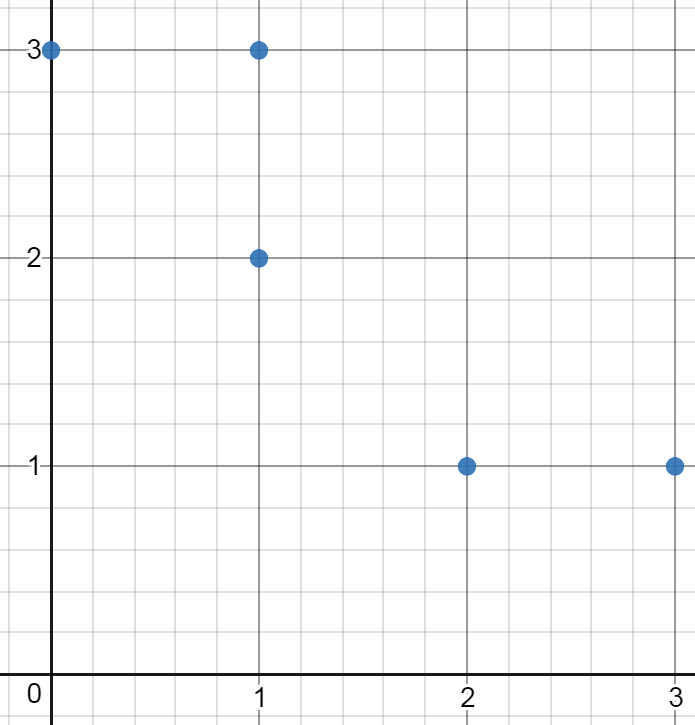
示例 3:
输入:[[0,3],[1,2],[3,1],[1,3],[2,1]] 输出:0 解释:没法从这些点中组成任何矩形。
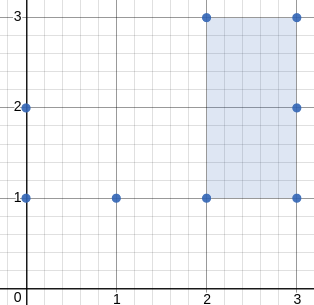
示例 4:
输入:[[3,1],[1,1],[0,1],[2,1],[3,3],[3,2],[0,2],[2,3]] 输出:2.00000 解释:最小面积的矩形出现在 [2,1],[2,3],[3,3],[3,1] 处,面积为 2。
提示:
1 <= points.length <= 500 <= points[i][0] <= 400000 <= points[i][1] <= 40000- 所有的点都是不同的。
- 与真实值误差不超过
10^-5的答案将视为正确结果。
我们用哈希表存放所有的点,然后枚举三个点
最后,如果找到满足条件的矩形,返回其中面积的最小值。否则,返回
时间复杂度
class Solution:
def minAreaFreeRect(self, points: List[List[int]]) -> float:
s = {(x, y) for x, y in points}
n = len(points)
ans = inf
for i in range(n):
x1, y1 = points[i]
for j in range(n):
if j != i:
x2, y2 = points[j]
for k in range(j + 1, n):
if k != i:
x3, y3 = points[k]
x4 = x2 - x1 + x3
y4 = y2 - y1 + y3
if (x4, y4) in s:
v21 = (x2 - x1, y2 - y1)
v31 = (x3 - x1, y3 - y1)
if v21[0] * v31[0] + v21[1] * v31[1] == 0:
w = sqrt(v21[0] ** 2 + v21[1] ** 2)
h = sqrt(v31[0] ** 2 + v31[1] ** 2)
ans = min(ans, w * h)
return 0 if ans == inf else ansclass Solution {
public double minAreaFreeRect(int[][] points) {
int n = points.length;
Set<Integer> s = new HashSet<>(n);
for (int[] p : points) {
s.add(f(p[0], p[1]));
}
double ans = Double.MAX_VALUE;
for (int i = 0; i < n; ++i) {
int x1 = points[i][0], y1 = points[i][1];
for (int j = 0; j < n; ++j) {
if (j != i) {
int x2 = points[j][0], y2 = points[j][1];
for (int k = j + 1; k < n; ++k) {
if (k != i) {
int x3 = points[k][0], y3 = points[k][1];
int x4 = x2 - x1 + x3, y4 = y2 - y1 + y3;
if (s.contains(f(x4, y4))) {
if ((x2 - x1) * (x3 - x1) + (y2 - y1) * (y3 - y1) == 0) {
int ww = (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1);
int hh = (x3 - x1) * (x3 - x1) + (y3 - y1) * (y3 - y1);
ans = Math.min(ans, Math.sqrt(1L * ww * hh));
}
}
}
}
}
}
}
return ans == Double.MAX_VALUE ? 0 : ans;
}
private int f(int x, int y) {
return x * 40001 + y;
}
}class Solution {
public:
double minAreaFreeRect(vector<vector<int>>& points) {
auto f = [](int x, int y) {
return x * 40001 + y;
};
int n = points.size();
unordered_set<int> s;
for (auto& p : points) {
s.insert(f(p[0], p[1]));
}
double ans = 1e20;
for (int i = 0; i < n; ++i) {
int x1 = points[i][0], y1 = points[i][1];
for (int j = 0; j < n; ++j) {
if (j != i) {
int x2 = points[j][0], y2 = points[j][1];
for (int k = j + 1; k < n; ++k) {
if (k != i) {
int x3 = points[k][0], y3 = points[k][1];
int x4 = x2 - x1 + x3, y4 = y2 - y1 + y3;
if (x4 >= 0 && x4 < 40000 && y4 >= 0 && y4 <= 40000 && s.count(f(x4, y4))) {
if ((x2 - x1) * (x3 - x1) + (y2 - y1) * (y3 - y1) == 0) {
int ww = (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1);
int hh = (x3 - x1) * (x3 - x1) + (y3 - y1) * (y3 - y1);
ans = min(ans, sqrt(1LL * ww * hh));
}
}
}
}
}
}
}
return ans == 1e20 ? 0 : ans;
}
};func minAreaFreeRect(points [][]int) float64 {
n := len(points)
f := func(x, y int) int {
return x*40001 + y
}
s := map[int]bool{}
for _, p := range points {
s[f(p[0], p[1])] = true
}
ans := 1e20
for i := 0; i < n; i++ {
x1, y1 := points[i][0], points[i][1]
for j := 0; j < n; j++ {
if j != i {
x2, y2 := points[j][0], points[j][1]
for k := j + 1; k < n; k++ {
if k != i {
x3, y3 := points[k][0], points[k][1]
x4, y4 := x2-x1+x3, y2-y1+y3
if s[f(x4, y4)] {
if (x2-x1)*(x3-x1)+(y2-y1)*(y3-y1) == 0 {
ww := (x2-x1)*(x2-x1) + (y2-y1)*(y2-y1)
hh := (x3-x1)*(x3-x1) + (y3-y1)*(y3-y1)
ans = math.Min(ans, math.Sqrt(float64(ww*hh)))
}
}
}
}
}
}
}
if ans == 1e20 {
return 0
}
return ans
}function minAreaFreeRect(points: number[][]): number {
const n = points.length;
const f = (x: number, y: number): number => x * 40001 + y;
const s: Set<number> = new Set();
for (const [x, y] of points) {
s.add(f(x, y));
}
let ans = Number.MAX_VALUE;
for (let i = 0; i < n; ++i) {
const [x1, y1] = points[i];
for (let j = 0; j < n; ++j) {
if (j !== i) {
const [x2, y2] = points[j];
for (let k = j + 1; k < n; ++k) {
if (k !== i) {
const [x3, y3] = points[k];
const x4 = x2 - x1 + x3;
const y4 = y2 - y1 + y3;
if (s.has(f(x4, y4))) {
if ((x2 - x1) * (x3 - x1) + (y2 - y1) * (y3 - y1) === 0) {
const ww = (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1);
const hh = (x3 - x1) * (x3 - x1) + (y3 - y1) * (y3 - y1);
ans = Math.min(ans, Math.sqrt(ww * hh));
}
}
}
}
}
}
}
return ans === Number.MAX_VALUE ? 0 : ans;
}