| comments | difficulty | edit_url | tags | ||||||
|---|---|---|---|---|---|---|---|---|---|
true |
困难 |
|
两位玩家分别扮演猫和老鼠,在一张 无向 图上进行游戏,两人轮流行动。
图的形式是:graph[a] 是一个列表,由满足 ab 是图中的一条边的所有节点 b 组成。
老鼠从节点 1 开始,第一个出发;猫从节点 2 开始,第二个出发。在节点 0 处有一个洞。
在每个玩家的行动中,他们 必须 沿着图中与所在当前位置连通的一条边移动。例如,如果老鼠在节点 1 ,那么它必须移动到 graph[1] 中的任一节点。
此外,猫无法移动到洞中(节点 0)。
然后,游戏在出现以下三种情形之一时结束:
- 如果猫和老鼠出现在同一个节点,猫获胜。
- 如果老鼠到达洞中,老鼠获胜。
- 如果某一位置重复出现(即,玩家的位置和移动顺序都与上一次行动相同),游戏平局。
给你一张图 graph ,并假设两位玩家都都以最佳状态参与游戏:
- 如果老鼠获胜,则返回
1; - 如果猫获胜,则返回
2; - 如果平局,则返回
0。
示例 1:
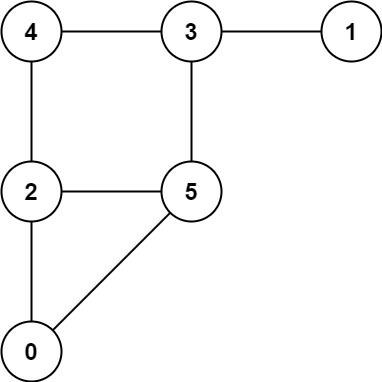
输入:graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]] 输出:0
示例 2:
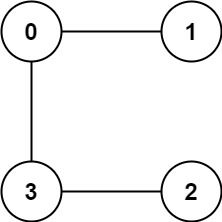
输入:graph = [[1,3],[0],[3],[0,2]] 输出:1
提示:
3 <= graph.length <= 501 <= graph[i].length < graph.length0 <= graph[i][j] < graph.lengthgraph[i][j] != igraph[i]互不相同- 猫和老鼠在游戏中总是可以移动
猫和老鼠的游戏中,状态由三个因素决定:老鼠的位置、猫的位置和移动方。根据游戏规则,可以直接确定胜负的边界状态有:
- 当猫和老鼠的位置相同时,猫获胜,为猫的必胜状态,老鼠的必败状态。
- 当老鼠位于洞时,老鼠获胜,为老鼠的必胜状态,猫的必败状态。
为了得到初始状态的游戏结果,需要从边界状态开始遍历所有的状态。每个状态包含老鼠的位置、猫的位置和移动方,根据当前状态可以得到上一轮的所有可能状态,上一轮状态的移动方和当前状态的移动方相反,上一轮状态的移动方在上一轮状态的位置和当前状态的位置不同。
我们用元组
- 如果本轮的移动方是老鼠,那么上一轮的移动方是猫,上一轮的老鼠位置是本轮老鼠位置,上一轮的猫位置是本轮猫位置的所有邻接点。
- 如果本轮的移动方是猫,那么上一轮的移动方是老鼠,上一轮的猫位置是本轮猫位置,上一轮的老鼠位置是本轮老鼠位置的所有邻接点。
初始时,除了边界状态以外,其他所有状态的结果都是未知的。我们从边界状态开始,对于每个状态,得到上一轮的所有可能状态并更新结果,更新的逻辑如下:
- 如果上一轮的移动方与本轮的获胜方相同,那么上一轮的移动方可以到达当前状态并获胜,直接更新上一轮的状态为本轮的获胜方。
- 如果上一轮的移动方与本轮的获胜方不同,且上一轮的移动方可以到达的所有状态都是上一轮的移动方的必败状态,那么我们将上一轮的状态更新为本轮的获胜方。
对于第
当所有状态的结果都更新完毕时,初始状态的结果即为最终结果。
时间复杂度
HOLE, MOUSE_START, CAT_START = 0, 1, 2
MOUSE_TURN, CAT_TURN = 0, 1
MOUSE_WIN, CAT_WIN, TIE = 1, 2, 0
class Solution:
def catMouseGame(self, graph: List[List[int]]) -> int:
def get_prev_states(state):
m, c, t = state
pt = t ^ 1
pre = []
if pt == CAT_TURN:
for pc in graph[c]:
if pc != HOLE:
pre.append((m, pc, pt))
else:
for pm in graph[m]:
pre.append((pm, c, pt))
return pre
n = len(graph)
res = [[[0, 0] for _ in range(n)] for _ in range(n)]
degree = [[[0, 0] for _ in range(n)] for _ in range(n)]
for i in range(n):
for j in range(1, n):
degree[i][j][MOUSE_TURN] = len(graph[i])
degree[i][j][CAT_TURN] = len(graph[j])
for j in graph[HOLE]:
degree[i][j][CAT_TURN] -= 1
q = deque()
for j in range(1, n):
res[0][j][MOUSE_TURN] = res[0][j][CAT_TURN] = MOUSE_WIN
q.append((0, j, MOUSE_TURN))
q.append((0, j, CAT_TURN))
for i in range(1, n):
res[i][i][MOUSE_TURN] = res[i][i][CAT_TURN] = CAT_WIN
q.append((i, i, MOUSE_TURN))
q.append((i, i, CAT_TURN))
while q:
state = q.popleft()
t = res[state[0]][state[1]][state[2]]
for prev_state in get_prev_states(state):
pm, pc, pt = prev_state
if res[pm][pc][pt] == TIE:
win = (t == MOUSE_WIN and pt == MOUSE_TURN) or (
t == CAT_WIN and pt == CAT_TURN
)
if win:
res[pm][pc][pt] = t
q.append(prev_state)
else:
degree[pm][pc][pt] -= 1
if degree[pm][pc][pt] == 0:
res[pm][pc][pt] = t
q.append(prev_state)
return res[MOUSE_START][CAT_START][MOUSE_TURN]class Solution {
private int n;
private int[][] g;
private int[][][] res;
private int[][][] degree;
private static final int HOLE = 0, MOUSE_START = 1, CAT_START = 2;
private static final int MOUSE_TURN = 0, CAT_TURN = 1;
private static final int MOUSE_WIN = 1, CAT_WIN = 2, TIE = 0;
public int catMouseGame(int[][] graph) {
n = graph.length;
g = graph;
res = new int[n][n][2];
degree = new int[n][n][2];
for (int i = 0; i < n; ++i) {
for (int j = 1; j < n; ++j) {
degree[i][j][MOUSE_TURN] = g[i].length;
degree[i][j][CAT_TURN] = g[j].length;
}
}
for (int i = 0; i < n; ++i) {
for (int j : g[HOLE]) {
--degree[i][j][CAT_TURN];
}
}
Deque<int[]> q = new ArrayDeque<>();
for (int j = 1; j < n; ++j) {
res[0][j][MOUSE_TURN] = MOUSE_WIN;
res[0][j][CAT_TURN] = MOUSE_WIN;
q.offer(new int[] {0, j, MOUSE_TURN});
q.offer(new int[] {0, j, CAT_TURN});
}
for (int i = 1; i < n; ++i) {
res[i][i][MOUSE_TURN] = CAT_WIN;
res[i][i][CAT_TURN] = CAT_WIN;
q.offer(new int[] {i, i, MOUSE_TURN});
q.offer(new int[] {i, i, CAT_TURN});
}
while (!q.isEmpty()) {
int[] state = q.poll();
int t = res[state[0]][state[1]][state[2]];
List<int[]> prevStates = getPrevStates(state);
for (var prevState : prevStates) {
int pm = prevState[0], pc = prevState[1], pt = prevState[2];
if (res[pm][pc][pt] == TIE) {
boolean win
= (t == MOUSE_WIN && pt == MOUSE_TURN) || (t == CAT_WIN && pt == CAT_TURN);
if (win) {
res[pm][pc][pt] = t;
q.offer(prevState);
} else {
if (--degree[pm][pc][pt] == 0) {
res[pm][pc][pt] = t;
q.offer(prevState);
}
}
}
}
}
return res[MOUSE_START][CAT_START][MOUSE_TURN];
}
private List<int[]> getPrevStates(int[] state) {
List<int[]> pre = new ArrayList<>();
int m = state[0], c = state[1], t = state[2];
int pt = t ^ 1;
if (pt == CAT_TURN) {
for (int pc : g[c]) {
if (pc != HOLE) {
pre.add(new int[] {m, pc, pt});
}
}
} else {
for (int pm : g[m]) {
pre.add(new int[] {pm, c, pt});
}
}
return pre;
}
}const int HOLE = 0;
const int MOUSE_START = 1;
const int CAT_START = 2;
const int MOUSE_TURN = 0;
const int CAT_TURN = 1;
const int MOUSE_WIN = 1;
const int CAT_WIN = 2;
const int TIE = 0;
class Solution {
public:
int catMouseGame(vector<vector<int>>& graph) {
int n = graph.size();
int res[n][n][2];
int degree[n][n][2];
memset(res, 0, sizeof res);
memset(degree, 0, sizeof degree);
for (int i = 0; i < n; ++i) {
for (int j = 1; j < n; ++j) {
degree[i][j][MOUSE_TURN] = graph[i].size();
degree[i][j][CAT_TURN] = graph[j].size();
}
for (int j : graph[HOLE]) {
--degree[i][j][CAT_TURN];
}
}
auto getPrevStates = [&](int m, int c, int t) {
int pt = t ^ 1;
vector<tuple<int, int, int>> pre;
if (pt == CAT_TURN) {
for (int pc : graph[c]) {
if (pc != HOLE) {
pre.emplace_back(m, pc, pt);
}
}
} else {
for (int pm : graph[m]) {
pre.emplace_back(pm, c, pt);
}
}
return pre;
};
queue<tuple<int, int, int>> q;
for (int j = 1; j < n; ++j) {
res[0][j][MOUSE_TURN] = res[0][j][CAT_TURN] = MOUSE_WIN;
q.emplace(0, j, MOUSE_TURN);
q.emplace(0, j, CAT_TURN);
}
for (int i = 1; i < n; ++i) {
res[i][i][MOUSE_TURN] = res[i][i][CAT_TURN] = CAT_WIN;
q.emplace(i, i, MOUSE_TURN);
q.emplace(i, i, CAT_TURN);
}
while (!q.empty()) {
auto [m, c, t] = q.front();
q.pop();
int x = res[m][c][t];
for (auto [pm, pc, pt] : getPrevStates(m, c, t)) {
if (res[pm][pc][pt] == TIE) {
bool win = (x == MOUSE_WIN && pt == MOUSE_TURN) || (x == CAT_WIN && pt == CAT_TURN);
if (win) {
res[pm][pc][pt] = x;
q.emplace(pm, pc, pt);
} else {
if (--degree[pm][pc][pt] == 0) {
res[pm][pc][pt] = x;
q.emplace(pm, pc, pt);
}
}
}
}
}
return res[MOUSE_START][CAT_START][MOUSE_TURN];
}
};const (
hole = 0
mouseStart = 1
catStart = 2
mouseTurn = 0
catTurn = 1
mouseWin = 1
catWin = 2
tie = 0
)
func catMouseGame(graph [][]int) int {
res := [50][50][2]int{}
degree := [50][50][2]int{}
n := len(graph)
for i := 0; i < n; i++ {
for j := 1; j < n; j++ {
degree[i][j][mouseTurn] = len(graph[i])
degree[i][j][catTurn] = len(graph[j])
}
for _, j := range graph[hole] {
degree[i][j][catTurn]--
}
}
type tuple struct{ m, c, t int }
q := []tuple{}
for j := 1; j < n; j++ {
res[0][j][mouseTurn], res[0][j][catTurn] = mouseWin, mouseWin
q = append(q, tuple{0, j, mouseTurn})
q = append(q, tuple{0, j, catTurn})
}
for i := 1; i < n; i++ {
res[i][i][mouseTurn], res[i][i][catTurn] = catWin, catWin
q = append(q, tuple{i, i, mouseTurn})
q = append(q, tuple{i, i, catTurn})
}
getPrevStates := func(m, c, t int) []tuple {
pre := []tuple{}
pt := t ^ 1
if pt == catTurn {
for _, pc := range graph[c] {
if pc != hole {
pre = append(pre, tuple{m, pc, pt})
}
}
} else {
for _, pm := range graph[m] {
pre = append(pre, tuple{pm, c, pt})
}
}
return pre
}
for len(q) > 0 {
state := q[0]
m, c, t := state.m, state.c, state.t
q = q[1:]
x := res[m][c][t]
for _, prevState := range getPrevStates(m, c, t) {
pm, pc, pt := prevState.m, prevState.c, prevState.t
if res[pm][pc][pt] == tie {
win := (x == mouseWin && pt == mouseTurn) || (x == catWin && pt == catTurn)
if win {
res[pm][pc][pt] = x
q = append(q, tuple{pm, pc, pt})
} else {
degree[pm][pc][pt]--
if degree[pm][pc][pt] == 0 {
res[pm][pc][pt] = x
q = append(q, tuple{pm, pc, pt})
}
}
}
}
}
return res[mouseStart][catStart][mouseTurn]
}