| comments | difficulty | edit_url | tags | ||
|---|---|---|---|---|---|
true |
中等 |
|
在一个 n x n 的矩阵 grid 中,除了在数组 mines 中给出的元素为 0,其他每个元素都为 1。mines[i] = [xi, yi]表示 grid[xi][yi] == 0
返回 grid 中包含 1 的最大的 轴对齐 加号标志的阶数 。如果未找到加号标志,则返回 0 。
一个 k 阶由 1 组成的 “轴对称”加号标志 具有中心网格 grid[r][c] == 1 ,以及4个从中心向上、向下、向左、向右延伸,长度为 k-1,由 1 组成的臂。注意,只有加号标志的所有网格要求为 1 ,别的网格可能为 0 也可能为 1 。
示例 1:
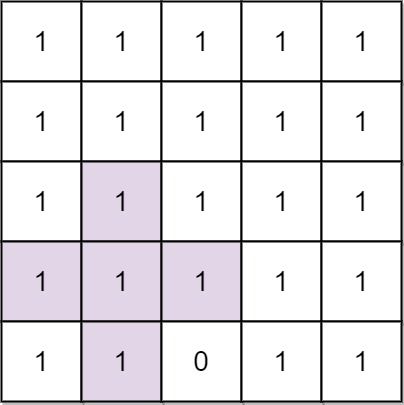
输入: n = 5, mines = [[4, 2]] 输出: 2 解释: 在上面的网格中,最大加号标志的阶只能是2。一个标志已在图中标出。
示例 2:
输入: n = 1, mines = [[0, 0]] 输出: 0 解释: 没有加号标志,返回 0 。
提示:
1 <= n <= 5001 <= mines.length <= 50000 <= xi, yi < n- 每一对
(xi, yi)都 不重复
我们定义
我们可以发现,对于每个
时间复杂度
class Solution:
def orderOfLargestPlusSign(self, n: int, mines: List[List[int]]) -> int:
dp = [[n] * n for _ in range(n)]
for x, y in mines:
dp[x][y] = 0
for i in range(n):
left = right = up = down = 0
for j, k in zip(range(n), reversed(range(n))):
left = left + 1 if dp[i][j] else 0
right = right + 1 if dp[i][k] else 0
up = up + 1 if dp[j][i] else 0
down = down + 1 if dp[k][i] else 0
dp[i][j] = min(dp[i][j], left)
dp[i][k] = min(dp[i][k], right)
dp[j][i] = min(dp[j][i], up)
dp[k][i] = min(dp[k][i], down)
return max(max(v) for v in dp)class Solution {
public int orderOfLargestPlusSign(int n, int[][] mines) {
int[][] dp = new int[n][n];
for (var e : dp) {
Arrays.fill(e, n);
}
for (var e : mines) {
dp[e[0]][e[1]] = 0;
}
for (int i = 0; i < n; ++i) {
int left = 0, right = 0, up = 0, down = 0;
for (int j = 0, k = n - 1; j < n; ++j, --k) {
left = dp[i][j] > 0 ? left + 1 : 0;
right = dp[i][k] > 0 ? right + 1 : 0;
up = dp[j][i] > 0 ? up + 1 : 0;
down = dp[k][i] > 0 ? down + 1 : 0;
dp[i][j] = Math.min(dp[i][j], left);
dp[i][k] = Math.min(dp[i][k], right);
dp[j][i] = Math.min(dp[j][i], up);
dp[k][i] = Math.min(dp[k][i], down);
}
}
return Arrays.stream(dp).flatMapToInt(Arrays::stream).max().getAsInt();
}
}class Solution {
public:
int orderOfLargestPlusSign(int n, vector<vector<int>>& mines) {
vector<vector<int>> dp(n, vector<int>(n, n));
for (auto& e : mines) dp[e[0]][e[1]] = 0;
for (int i = 0; i < n; ++i) {
int left = 0, right = 0, up = 0, down = 0;
for (int j = 0, k = n - 1; j < n; ++j, --k) {
left = dp[i][j] ? left + 1 : 0;
right = dp[i][k] ? right + 1 : 0;
up = dp[j][i] ? up + 1 : 0;
down = dp[k][i] ? down + 1 : 0;
dp[i][j] = min(dp[i][j], left);
dp[i][k] = min(dp[i][k], right);
dp[j][i] = min(dp[j][i], up);
dp[k][i] = min(dp[k][i], down);
}
}
int ans = 0;
for (auto& e : dp) ans = max(ans, *max_element(e.begin(), e.end()));
return ans;
}
};func orderOfLargestPlusSign(n int, mines [][]int) (ans int) {
dp := make([][]int, n)
for i := range dp {
dp[i] = make([]int, n)
for j := range dp[i] {
dp[i][j] = n
}
}
for _, e := range mines {
dp[e[0]][e[1]] = 0
}
for i := 0; i < n; i++ {
var left, right, up, down int
for j, k := 0, n-1; j < n; j, k = j+1, k-1 {
left, right, up, down = left+1, right+1, up+1, down+1
if dp[i][j] == 0 {
left = 0
}
if dp[i][k] == 0 {
right = 0
}
if dp[j][i] == 0 {
up = 0
}
if dp[k][i] == 0 {
down = 0
}
dp[i][j] = min(dp[i][j], left)
dp[i][k] = min(dp[i][k], right)
dp[j][i] = min(dp[j][i], up)
dp[k][i] = min(dp[k][i], down)
}
}
for _, e := range dp {
ans = max(ans, slices.Max(e))
}
return
}