comments

difficulty

edit_url

699. 掉落的方块

题目描述

在二维平面上的 x 轴上，放置着一些方块。

给你一个二维整数数组 positions ，其中 positions[i] = [left_i, sideLength_i] 表示：第 i 个方块边长为 sideLength_i ，其左侧边与 x 轴上坐标点 left_i 对齐。

每个方块都从一个比目前所有的落地方块更高的高度掉落而下。方块沿 y 轴负方向下落，直到着陆到 另一个正方形的顶边 或者是 x 轴上 。一个方块仅仅是擦过另一个方块的左侧边或右侧边不算着陆。一旦着陆，它就会固定在原地，无法移动。

在每个方块掉落后，你必须记录目前所有已经落稳的 方块堆叠的最高高度 。

返回一个整数数组 ans ，其中 ans[i] 表示在第 i 块方块掉落后堆叠的最高高度。

示例 1：

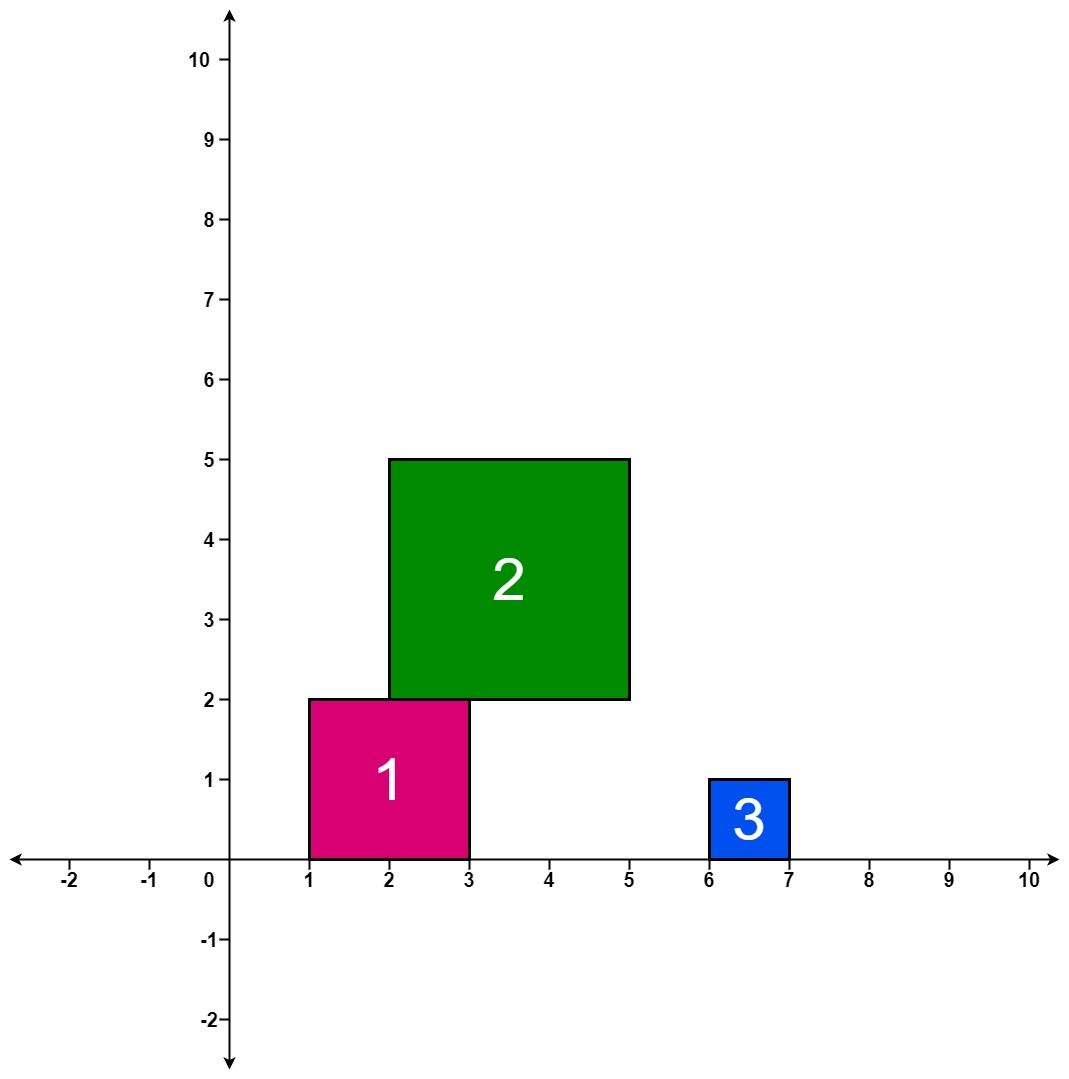
输入：positions = [[1,2],[2,3],[6,1]]
输出：[2,5,5]
解释：
第 1 个方块掉落后，最高的堆叠由方块 1 组成，堆叠的最高高度为 2 。
第 2 个方块掉落后，最高的堆叠由方块 1 和 2 组成，堆叠的最高高度为 5 。
第 3 个方块掉落后，最高的堆叠仍然由方块 1 和 2 组成，堆叠的最高高度为 5 。
因此，返回 [2, 5, 5] 作为答案。

示例 2：

输入：positions = [[100,100],[200,100]]
输出：[100,100]
解释：
第 1 个方块掉落后，最高的堆叠由方块 1 组成，堆叠的最高高度为 100 。
第 2 个方块掉落后，最高的堆叠可以由方块 1 组成也可以由方块 2 组成，堆叠的最高高度为 100 。
因此，返回 [100, 100] 作为答案。
注意，方块 2 擦过方块 1 的右侧边，但不会算作在方块 1 上着陆。

提示：

1 <= positions.length <= 1000
1 <= left_i <= 10⁸
1 <= sideLength_i <= 10⁶

解法

方法一：线段树

根据题目描述，我们需要维护一个区间集合，支持区间的修改和查询操作。这种情况下，我们可以使用线段树来解决。

线段树将整个区间分割为多个不连续的子区间，子区间的数量不超过 $\log(width)$，其中 $width$ 是区间的长度。更新某个元素的值，只需要更新 $\log(width)$ 个区间，并且这些区间都包含在一个包含该元素的大区间内。区间修改时，需要使用懒标记保证效率。

线段树的每个节点代表一个区间；
线段树具有唯一的根节点，代表的区间是整个统计范围，如 $[1, n]$；
线段树的每个叶子节点代表一个长度为 1 的元区间 $[x, x]$；
对于每个内部节点 $[l, r]$，它的左儿子是 $[l, mid]$，右儿子是 $[mid + 1, r]$, 其中 $\textit{mid} = \frac{l + r}{2}$；

对于本题，线段树节点维护的信息有：

区间中方块的最大高度 $v$
懒标记 $add$

另外，由于数轴范围很大，达到 $10^8$，因此我们采用动态开点。

时间复杂度方面，每次查询和修改的时间复杂度为 $O(\log n)$，总时间复杂度为 $O(n \log n)$。空间复杂度为 $O(n)$。

Python3

class Node:
    def __init__(self, l, r):
        self.left = None
        self.right = None
        self.l = l
        self.r = r
        self.mid = (l + r) >> 1
        self.v = 0
        self.add = 0


class SegmentTree:
    def __init__(self):
        self.root = Node(1, int(1e9))

    def modify(self, l, r, v, node=None):
        if l > r:
            return
        if node is None:
            node = self.root
        if node.l >= l and node.r <= r:
            node.v = v
            node.add = v
            return
        self.pushdown(node)
        if l <= node.mid:
            self.modify(l, r, v, node.left)
        if r > node.mid:
            self.modify(l, r, v, node.right)
        self.pushup(node)

    def query(self, l, r, node=None):
        if l > r:
            return 0
        if node is None:
            node = self.root
        if node.l >= l and node.r <= r:
            return node.v
        self.pushdown(node)
        v = 0
        if l <= node.mid:
            v = max(v, self.query(l, r, node.left))
        if r > node.mid:
            v = max(v, self.query(l, r, node.right))
        return v

    def pushup(self, node):
        node.v = max(node.left.v, node.right.v)

    def pushdown(self, node):
        if node.left is None:
            node.left = Node(node.l, node.mid)
        if node.right is None:
            node.right = Node(node.mid + 1, node.r)
        if node.add:
            node.left.v = node.add
            node.right.v = node.add
            node.left.add = node.add
            node.right.add = node.add
            node.add = 0


class Solution:
    def fallingSquares(self, positions: List[List[int]]) -> List[int]:
        ans = []
        mx = 0
        tree = SegmentTree()
        for l, w in positions:
            r = l + w - 1
            h = tree.query(l, r) + w
            mx = max(mx, h)
            ans.append(mx)
            tree.modify(l, r, h)
        return ans

Java

class Node {
    Node left;
    Node right;
    int l;
    int r;
    int mid;
    int v;
    int add;
    public Node(int l, int r) {
        this.l = l;
        this.r = r;
        this.mid = (l + r) >> 1;
    }
}

class SegmentTree {
    private Node root = new Node(1, (int) 1e9);

    public SegmentTree() {
    }

    public void modify(int l, int r, int v) {
        modify(l, r, v, root);
    }

    public void modify(int l, int r, int v, Node node) {
        if (l > r) {
            return;
        }
        if (node.l >= l && node.r <= r) {
            node.v = v;
            node.add = v;
            return;
        }
        pushdown(node);
        if (l <= node.mid) {
            modify(l, r, v, node.left);
        }
        if (r > node.mid) {
            modify(l, r, v, node.right);
        }
        pushup(node);
    }

    public int query(int l, int r) {
        return query(l, r, root);
    }

    public int query(int l, int r, Node node) {
        if (l > r) {
            return 0;
        }
        if (node.l >= l && node.r <= r) {
            return node.v;
        }
        pushdown(node);
        int v = 0;
        if (l <= node.mid) {
            v = Math.max(v, query(l, r, node.left));
        }
        if (r > node.mid) {
            v = Math.max(v, query(l, r, node.right));
        }
        return v;
    }

    public void pushup(Node node) {
        node.v = Math.max(node.left.v, node.right.v);
    }

    public void pushdown(Node node) {
        if (node.left == null) {
            node.left = new Node(node.l, node.mid);
        }
        if (node.right == null) {
            node.right = new Node(node.mid + 1, node.r);
        }
        if (node.add != 0) {
            Node left = node.left, right = node.right;
            left.add = node.add;
            right.add = node.add;
            left.v = node.add;
            right.v = node.add;
            node.add = 0;
        }
    }
}

class Solution {
    public List<Integer> fallingSquares(int[][] positions) {
        List<Integer> ans = new ArrayList<>();
        SegmentTree tree = new SegmentTree();
        int mx = 0;
        for (int[] p : positions) {
            int l = p[0], w = p[1], r = l + w - 1;
            int h = tree.query(l, r) + w;
            mx = Math.max(mx, h);
            ans.add(mx);
            tree.modify(l, r, h);
        }
        return ans;
    }
}

C++

class Node {
public:
    Node* left;
    Node* right;
    int l;
    int r;
    int mid;
    int v;
    int add;

    Node(int l, int r) {
        this->l = l;
        this->r = r;
        this->mid = (l + r) >> 1;
        this->left = this->right = nullptr;
        v = add = 0;
    }
};

class SegmentTree {
private:
    Node* root;

public:
    SegmentTree() {
        root = new Node(1, 1e9);
    }

    void modify(int l, int r, int v) {
        modify(l, r, v, root);
    }

    void modify(int l, int r, int v, Node* node) {
        if (l > r) return;
        if (node->l >= l && node->r <= r) {
            node->v = v;
            node->add = v;
            return;
        }
        pushdown(node);
        if (l <= node->mid) modify(l, r, v, node->left);
        if (r > node->mid) modify(l, r, v, node->right);
        pushup(node);
    }

    int query(int l, int r) {
        return query(l, r, root);
    }

    int query(int l, int r, Node* node) {
        if (l > r) return 0;
        if (node->l >= l && node->r <= r) return node->v;
        pushdown(node);
        int v = 0;
        if (l <= node->mid) v = max(v, query(l, r, node->left));
        if (r > node->mid) v = max(v, query(l, r, node->right));
        return v;
    }

    void pushup(Node* node) {
        node->v = max(node->left->v, node->right->v);
    }

    void pushdown(Node* node) {
        if (!node->left) node->left = new Node(node->l, node->mid);
        if (!node->right) node->right = new Node(node->mid + 1, node->r);
        if (node->add) {
            Node* left = node->left;
            Node* right = node->right;
            left->v = node->add;
            right->v = node->add;
            left->add = node->add;
            right->add = node->add;
            node->add = 0;
        }
    }
};

class Solution {
public:
    vector<int> fallingSquares(vector<vector<int>>& positions) {
        vector<int> ans;
        SegmentTree* tree = new SegmentTree();
        int mx = 0;
        for (auto& p : positions) {
            int l = p[0], w = p[1], r = l + w - 1;
            int h = tree->query(l, r) + w;
            mx = max(mx, h);
            ans.push_back(mx);
            tree->modify(l, r, h);
        }
        return ans;
    }
};

Go

type node struct {
	left      *node
	right     *node
	l, mid, r int
	v, add    int
}

func newNode(l, r int) *node {
	return &node{
		l:   l,
		r:   r,
		mid: (l + r) >> 1,
	}
}

type segmentTree struct {
	root *node
}

func newSegmentTree() *segmentTree {
	return &segmentTree{
		root: newNode(1, 1e9),
	}
}

func (t *segmentTree) modify(l, r, v int, n *node) {
	if l > r {
		return
	}
	if n.l >= l && n.r <= r {
		n.v = v
		n.add = v
		return
	}
	t.pushdown(n)
	if l <= n.mid {
		t.modify(l, r, v, n.left)
	}
	if r > n.mid {
		t.modify(l, r, v, n.right)
	}
	t.pushup(n)
}

func (t *segmentTree) query(l, r int, n *node) int {
	if l > r {
		return 0
	}
	if n.l >= l && n.r <= r {
		return n.v
	}
	t.pushdown(n)
	v := 0
	if l <= n.mid {
		v = max(v, t.query(l, r, n.left))
	}
	if r > n.mid {
		v = max(v, t.query(l, r, n.right))
	}
	return v
}

func (t *segmentTree) pushup(n *node) {
	n.v = max(n.left.v, n.right.v)
}

func (t *segmentTree) pushdown(n *node) {
	if n.left == nil {
		n.left = newNode(n.l, n.mid)
	}
	if n.right == nil {
		n.right = newNode(n.mid+1, n.r)
	}
	if n.add != 0 {
		n.left.add = n.add
		n.right.add = n.add
		n.left.v = n.add
		n.right.v = n.add
		n.add = 0
	}
}

func fallingSquares(positions [][]int) []int {
	ans := make([]int, len(positions))
	t := newSegmentTree()
	mx := 0
	for i, p := range positions {
		l, w, r := p[0], p[1], p[0]+p[1]-1
		h := t.query(l, r, t.root) + w
		mx = max(mx, h)
		ans[i] = mx
		t.modify(l, r, h, t.root)
	}
	return ans
}

TypeScript

class Node {
    left: Node | null = null;
    right: Node | null = null;
    l: number;
    r: number;
    mid: number;
    v: number = 0;
    add: number = 0;

    constructor(l: number, r: number) {
        this.l = l;
        this.r = r;
        this.mid = (l + r) >> 1;
    }
}

class SegmentTree {
    private root: Node = new Node(1, 1e9);

    public modify(l: number, r: number, v: number): void {
        this.modifyNode(l, r, v, this.root);
    }

    private modifyNode(l: number, r: number, v: number, node: Node): void {
        if (l > r) {
            return;
        }
        if (node.l >= l && node.r <= r) {
            node.v = v;
            node.add = v;
            return;
        }
        this.pushdown(node);
        if (l <= node.mid) {
            this.modifyNode(l, r, v, node.left!);
        }
        if (r > node.mid) {
            this.modifyNode(l, r, v, node.right!);
        }
        this.pushup(node);
    }

    public query(l: number, r: number): number {
        return this.queryNode(l, r, this.root);
    }

    private queryNode(l: number, r: number, node: Node): number {
        if (l > r) {
            return 0;
        }
        if (node.l >= l && node.r <= r) {
            return node.v;
        }
        this.pushdown(node);
        let v = 0;
        if (l <= node.mid) {
            v = Math.max(v, this.queryNode(l, r, node.left!));
        }
        if (r > node.mid) {
            v = Math.max(v, this.queryNode(l, r, node.right!));
        }
        return v;
    }

    private pushup(node: Node): void {
        node.v = Math.max(node.left!.v, node.right!.v);
    }

    private pushdown(node: Node): void {
        if (node.left == null) {
            node.left = new Node(node.l, node.mid);
        }
        if (node.right == null) {
            node.right = new Node(node.mid + 1, node.r);
        }
        if (node.add != 0) {
            let left = node.left,
                right = node.right;
            left!.add = node.add;
            right!.add = node.add;
            left!.v = node.add;
            right!.v = node.add;
            node.add = 0;
        }
    }
}

function fallingSquares(positions: number[][]): number[] {
    const ans: number[] = [];
    const tree = new SegmentTree();
    let mx = 0;
    for (const [l, w] of positions) {
        const r = l + w - 1;
        const h = tree.query(l, r) + w;
        mx = Math.max(mx, h);
        ans.push(mx);
        tree.modify(l, r, h);
    }
    return ans;
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README.md

README.md

699. 掉落的方块

题目描述

解法

方法一：线段树

Python3

Java

C++

Go

TypeScript

Files

README.md

Latest commit

History

README.md

File metadata and controls

699. 掉落的方块

题目描述

解法

方法一：线段树

Python3

Java

C++

Go

TypeScript