| comments | difficulty | edit_url | tags | ||
|---|---|---|---|---|---|
true |
困难 |
|
给你一个数组 rectangles ,其中 rectangles[i] = [xi, yi, ai, bi] 表示一个坐标轴平行的矩形。这个矩形的左下顶点是 (xi, yi) ,右上顶点是 (ai, bi) 。
如果所有矩形一起精确覆盖了某个矩形区域,则返回 true ;否则,返回 false 。
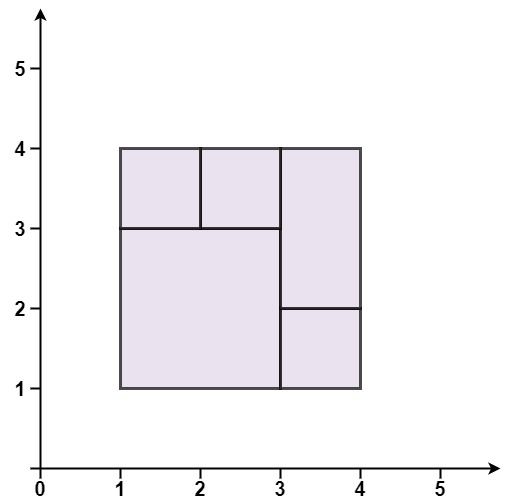
示例 1:
输入:rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]] 输出:true 解释:5 个矩形一起可以精确地覆盖一个矩形区域。
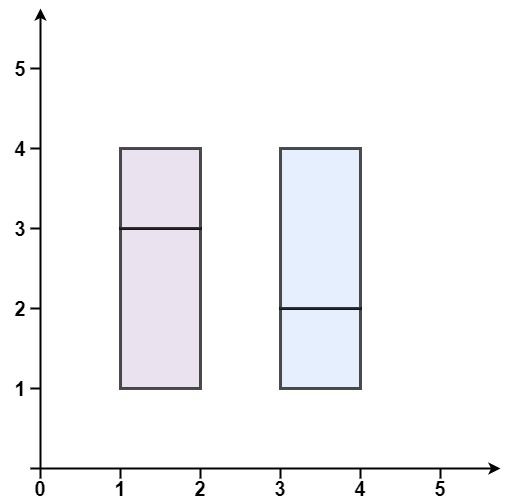
示例 2:
输入:rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]] 输出:false 解释:两个矩形之间有间隔,无法覆盖成一个矩形。
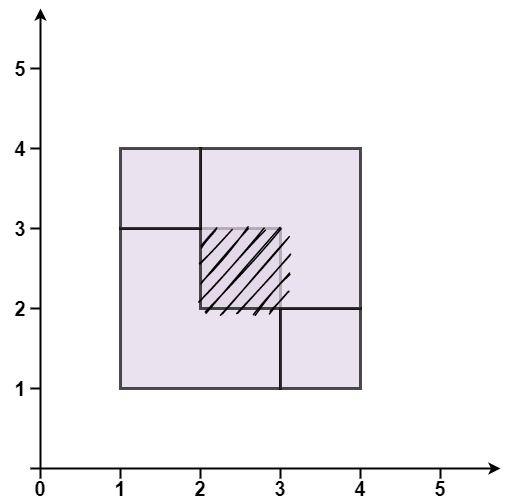
示例 3:
输入:rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]] 输出:false 解释:因为中间有相交区域,虽然形成了矩形,但不是精确覆盖。
提示:
1 <= rectangles.length <= 2 * 104rectangles[i].length == 4-105 <= xi < ai <= 105-105 <= yi < bi <= 105
class Solution:
def isRectangleCover(self, rectangles: List[List[int]]) -> bool:
area = 0
minX, minY = rectangles[0][0], rectangles[0][1]
maxX, maxY = rectangles[0][2], rectangles[0][3]
cnt = defaultdict(int)
for r in rectangles:
area += (r[2] - r[0]) * (r[3] - r[1])
minX = min(minX, r[0])
minY = min(minY, r[1])
maxX = max(maxX, r[2])
maxY = max(maxY, r[3])
cnt[(r[0], r[1])] += 1
cnt[(r[0], r[3])] += 1
cnt[(r[2], r[3])] += 1
cnt[(r[2], r[1])] += 1
if (
area != (maxX - minX) * (maxY - minY)
or cnt[(minX, minY)] != 1
or cnt[(minX, maxY)] != 1
or cnt[(maxX, maxY)] != 1
or cnt[(maxX, minY)] != 1
):
return False
del cnt[(minX, minY)], cnt[(minX, maxY)], cnt[(maxX, maxY)], cnt[(maxX, minY)]
return all(c == 2 or c == 4 for c in cnt.values())class Solution {
public boolean isRectangleCover(int[][] rectangles) {
long area = 0;
int minX = rectangles[0][0], minY = rectangles[0][1];
int maxX = rectangles[0][2], maxY = rectangles[0][3];
Map<Pair, Integer> cnt = new HashMap<>();
for (int[] r : rectangles) {
area += (r[2] - r[0]) * (r[3] - r[1]);
minX = Math.min(minX, r[0]);
minY = Math.min(minY, r[1]);
maxX = Math.max(maxX, r[2]);
maxY = Math.max(maxY, r[3]);
cnt.merge(new Pair(r[0], r[1]), 1, Integer::sum);
cnt.merge(new Pair(r[0], r[3]), 1, Integer::sum);
cnt.merge(new Pair(r[2], r[3]), 1, Integer::sum);
cnt.merge(new Pair(r[2], r[1]), 1, Integer::sum);
}
if (area != (long) (maxX - minX) * (maxY - minY)
|| cnt.getOrDefault(new Pair(minX, minY), 0) != 1
|| cnt.getOrDefault(new Pair(minX, maxY), 0) != 1
|| cnt.getOrDefault(new Pair(maxX, maxY), 0) != 1
|| cnt.getOrDefault(new Pair(maxX, minY), 0) != 1) {
return false;
}
cnt.remove(new Pair(minX, minY));
cnt.remove(new Pair(minX, maxY));
cnt.remove(new Pair(maxX, maxY));
cnt.remove(new Pair(maxX, minY));
return cnt.values().stream().allMatch(c -> c == 2 || c == 4);
}
private static class Pair {
final int first;
final int second;
Pair(int first, int second) {
this.first = first;
this.second = second;
}
@Override
public boolean equals(Object o) {
if (this == o) {
return true;
}
if (o == null || getClass() != o.getClass()) {
return false;
}
Pair pair = (Pair) o;
return first == pair.first && second == pair.second;
}
@Override
public int hashCode() {
return Objects.hash(first, second);
}
}
}#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
bool isRectangleCover(vector<vector<int>>& rectangles) {
long long area = 0;
int minX = rectangles[0][0], minY = rectangles[0][1];
int maxX = rectangles[0][2], maxY = rectangles[0][3];
using pii = pair<int, int>;
map<pii, int> cnt;
for (auto& r : rectangles) {
area += (r[2] - r[0]) * (r[3] - r[1]);
minX = min(minX, r[0]);
minY = min(minY, r[1]);
maxX = max(maxX, r[2]);
maxY = max(maxY, r[3]);
++cnt[{r[0], r[1]}];
++cnt[{r[0], r[3]}];
++cnt[{r[2], r[3]}];
++cnt[{r[2], r[1]}];
}
if (area != (long long) (maxX - minX) * (maxY - minY) || cnt[{minX, minY}] != 1 || cnt[{minX, maxY}] != 1 || cnt[{maxX, maxY}] != 1 || cnt[{maxX, minY}] != 1) {
return false;
}
cnt.erase({minX, minY});
cnt.erase({minX, maxY});
cnt.erase({maxX, maxY});
cnt.erase({maxX, minY});
return all_of(cnt.begin(), cnt.end(), [](pair<pii, int> e) {
return e.second == 2 || e.second == 4;
});
}
};type pair struct {
first int
second int
}
func isRectangleCover(rectangles [][]int) bool {
area := 0
minX, minY := rectangles[0][0], rectangles[0][1]
maxX, maxY := rectangles[0][2], rectangles[0][3]
cnt := make(map[pair]int)
for _, r := range rectangles {
area += (r[2] - r[0]) * (r[3] - r[1])
minX = min(minX, r[0])
minY = min(minY, r[1])
maxX = max(maxX, r[2])
maxY = max(maxY, r[3])
cnt[pair{r[0], r[1]}]++
cnt[pair{r[0], r[3]}]++
cnt[pair{r[2], r[3]}]++
cnt[pair{r[2], r[1]}]++
}
if area != (maxX-minX)*(maxY-minY) ||
cnt[pair{minX, minY}] != 1 ||
cnt[pair{minX, maxY}] != 1 ||
cnt[pair{maxX, maxY}] != 1 ||
cnt[pair{maxX, minY}] != 1 {
return false
}
delete(cnt, pair{minX, minY})
delete(cnt, pair{minX, maxY})
delete(cnt, pair{maxX, maxY})
delete(cnt, pair{maxX, minY})
for _, c := range cnt {
if c != 2 && c != 4 {
return false
}
}
return true
}