README.md

comments	difficulty	edit_url	tags
true	中等	https://github.com/doocs/leetcode/edit/main/solution/0300-0399/0356.Line%20Reflection/README.md	数组 哈希表 数学

356. 直线镜像 🔒

English Version

题目描述

在一个二维平面空间中，给你 n 个点的坐标。问，是否能找出一条平行于 y 轴的直线，让这些点关于这条直线成镜像排布？

注意：题目数据中可能有重复的点。

 

示例 1：

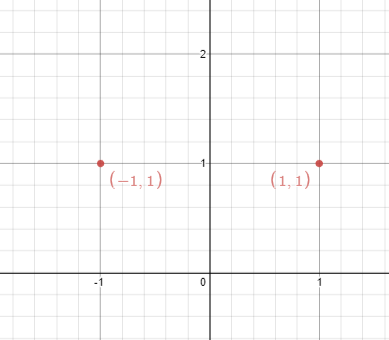
输入：points = [[1,1],[-1,1]]
输出：true
解释：可以找出 x = 0 这条线。

示例 2：

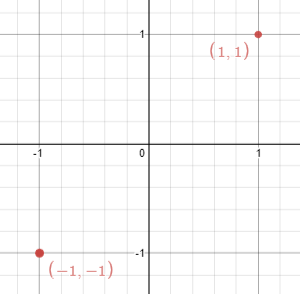
输入：points = [[1,1],[-1,-1]]
输出：false
解释：无法找出这样一条线。

 

提示：

• n == points.length
• 1 <= n <= 10^4
• -10^8 <= points[i][j] <= 10^8

 

进阶：你能找到比 O(n²) 更优的解法吗?

解法

方法一：哈希表

我们先找出所有点中的最小、最大的 $x$ 坐标 $minX$ 和 $maxX$。若存在满足条件的直线，则直线 $x = (minX + maxX) / 2$，或者说 $s = minX + maxX$。

接下来，我们遍历每个点 $(x, y)，若 $(s - x, y)$ 不在点集里，说明不满足条件，直接返回 false。遍历结束返回 true。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是数组 $points$ 的长度。

Python3

class Solution:
    def isReflected(self, points: List[List[int]]) -> bool:
        min_x, max_x = inf, -inf
        point_set = set()
        for x, y in points:
            min_x = min(min_x, x)
            max_x = max(max_x, x)
            point_set.add((x, y))
        s = min_x + max_x
        return all((s - x, y) in point_set for x, y in points)

Java

class Solution {
    public boolean isReflected(int[][] points) {
        final int inf = 1 << 30;
        int minX = inf, maxX = -inf;
        Set<List<Integer>> pointSet = new HashSet<>();
        for (int[] p : points) {
            minX = Math.min(minX, p[0]);
            maxX = Math.max(maxX, p[0]);
            pointSet.add(List.of(p[0], p[1]));
        }
        int s = minX + maxX;
        for (int[] p : points) {
            if (!pointSet.contains(List.of(s - p[0], p[1]))) {
                return false;
            }
        }
        return true;
    }
}

C++

class Solution {
public:
    bool isReflected(vector<vector<int>>& points) {
        const int inf = 1 << 30;
        int minX = inf, maxX = -inf;
        set<pair<int, int>> pointSet;
        for (auto& p : points) {
            minX = min(minX, p[0]);
            maxX = max(maxX, p[0]);
            pointSet.insert({p[0], p[1]});
        }
        int s = minX + maxX;
        for (auto& p : points) {
            if (!pointSet.count({s - p[0], p[1]})) {
                return false;
            }
        }
        return true;
    }
};

Go

func isReflected(points [][]int) bool {
	const inf = 1 << 30
	minX, maxX := inf, -inf
	pointSet := map[[2]int]bool{}
	for _, p := range points {
		minX = min(minX, p[0])
		maxX = max(maxX, p[0])
		pointSet[[2]int{p[0], p[1]}] = true
	}
	s := minX + maxX
	for _, p := range points {
		if !pointSet[[2]int{s - p[0], p[1]}] {
			return false
		}
	}
	return true
}