| comments | difficulty | edit_url | tags | ||||
|---|---|---|---|---|---|---|---|
true |
简单 |
|
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
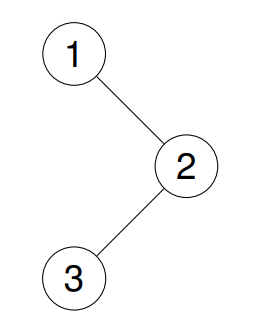
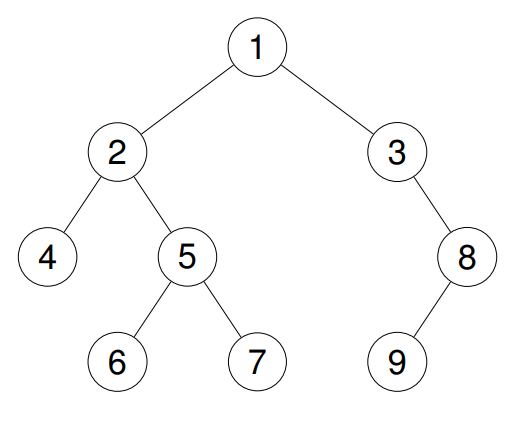
示例 1:
示例 2:
示例 3:
输入:root = []
输出:[]
示例 4:
输入:root = [1]
输出:[1]
提示:
- 树中节点的数目在范围
[0, 100]内 -100 <= Node.val <= 100
进阶:递归算法很简单,你可以通过迭代算法完成吗?
我们先递归左右子树,然后再访问根节点。
时间复杂度
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
def dfs(root):
if root is None:
return
dfs(root.left)
dfs(root.right)
ans.append(root.val)
ans = []
dfs(root)
return ans/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private List<Integer> ans = new ArrayList<>();
public List<Integer> postorderTraversal(TreeNode root) {
dfs(root);
return ans;
}
private void dfs(TreeNode root) {
if (root == null) {
return;
}
dfs(root.left);
dfs(root.right);
ans.add(root.val);
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ans;
function<void(TreeNode*)> dfs = [&](TreeNode* root) {
if (!root) {
return;
}
dfs(root->left);
dfs(root->right);
ans.push_back(root->val);
};
dfs(root);
return ans;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func postorderTraversal(root *TreeNode) (ans []int) {
var dfs func(*TreeNode)
dfs = func(root *TreeNode) {
if root == nil {
return
}
dfs(root.Left)
dfs(root.Right)
ans = append(ans, root.Val)
}
dfs(root)
return
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function postorderTraversal(root: TreeNode | null): number[] {
const ans: number[] = [];
const dfs = (root: TreeNode | null) => {
if (!root) {
return;
}
dfs(root.left);
dfs(root.right);
ans.push(root.val);
};
dfs(root);
return ans;
}// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
fn dfs(root: &Option<Rc<RefCell<TreeNode>>>, ans: &mut Vec<i32>) {
if root.is_none() {
return;
}
let node = root.as_ref().unwrap().borrow();
Self::dfs(&node.left, ans);
Self::dfs(&node.right, ans);
ans.push(node.val);
}
pub fn postorder_traversal(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
let mut ans = vec![];
Self::dfs(&root, &mut ans);
ans
}
}先序遍历的顺序是:根、左、右,如果我们改变左右孩子的顺序,就能将顺序变成:根、右、左。最后再将结果反转一下,就得到了后序遍历的结果。
因此,栈实现非递归遍历的思路如下:
- 定义一个栈
$stk$ ,先将根节点压入栈 - 若栈不为空,每次从栈中弹出一个节点
- 处理该节点
- 先把节点左孩子压入栈,接着把节点右孩子压入栈(如果有孩子节点)
- 重复 2-4
- 将结果反转,得到后序遍历的结果
时间复杂度
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
ans = []
if root is None:
return ans
stk = [root]
while stk:
node = stk.pop()
ans.append(node.val)
if node.left:
stk.append(node.left)
if node.right:
stk.append(node.right)
return ans[::-1]/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
LinkedList<Integer> ans = new LinkedList<>();
if (root == null) {
return ans;
}
Deque<TreeNode> stk = new ArrayDeque<>();
stk.push(root);
while (!stk.isEmpty()) {
TreeNode node = stk.pop();
ans.addFirst(node.val);
if (node.left != null) {
stk.push(node.left);
}
if (node.right != null) {
stk.push(node.right);
}
}
return ans;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ans;
if (!root) {
return ans;
}
stack<TreeNode*> stk;
stk.push(root);
while (stk.size()) {
auto node = stk.top();
stk.pop();
ans.push_back(node->val);
if (node->left) {
stk.push(node->left);
}
if (node->right) {
stk.push(node->right);
}
}
reverse(ans.begin(), ans.end());
return ans;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func postorderTraversal(root *TreeNode) (ans []int) {
if root == nil {
return
}
stk := []*TreeNode{root}
for len(stk) > 0 {
node := stk[len(stk)-1]
stk = stk[:len(stk)-1]
ans = append(ans, node.Val)
if node.Left != nil {
stk = append(stk, node.Left)
}
if node.Right != nil {
stk = append(stk, node.Right)
}
}
for i, j := 0, len(ans)-1; i < j; i, j = i+1, j-1 {
ans[i], ans[j] = ans[j], ans[i]
}
return
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function postorderTraversal(root: TreeNode | null): number[] {
const ans: number[] = [];
if (!root) {
return ans;
}
const stk: TreeNode[] = [root];
while (stk.length) {
const { left, right, val } = stk.pop();
ans.push(val);
left && stk.push(left);
right && stk.push(right);
}
ans.reverse();
return ans;
}Morris 遍历无需使用栈,空间复杂度为
遍历二叉树节点,
- 若当前节点
root的右子树为空,将当前节点值添加至结果列表$ans$ 中,并将当前节点更新为root.left - 若当前节点
root的右子树不为空,找到右子树的最左节点next(也即是root节点在中序遍历下的后继节点):- 若后继节点
next的左子树为空,将当前节点值添加至结果列表$ans$ 中,然后将后继节点的左子树指向当前节点root,并将当前节点更新为root.right。 - 若后继节点
next的左子树不为空,将后继节点左子树指向空(即解除next与root的指向关系),并将当前节点更新为root.left。
- 若后继节点
- 循环以上步骤,直至二叉树节点为空,遍历结束。
- 最后返回结果列表的逆序即可。
Morris 后序遍历跟 Morris 前序遍历思路一致,只是将前序的“根左右”变为“根右左”,最后逆序结果即可变成“左右根”。
时间复杂度
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
ans = []
while root:
if root.right is None:
ans.append(root.val)
root = root.left
else:
next = root.right
while next.left and next.left != root:
next = next.left
if next.left != root:
ans.append(root.val)
next.left = root
root = root.right
else:
next.left = None
root = root.left
return ans[::-1]/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
LinkedList<Integer> ans = new LinkedList<>();
while (root != null) {
if (root.right == null) {
ans.addFirst(root.val);
root = root.left;
} else {
TreeNode next = root.right;
while (next.left != null && next.left != root) {
next = next.left;
}
if (next.left == null) {
ans.addFirst(root.val);
next.left = root;
root = root.right;
} else {
next.left = null;
root = root.left;
}
}
}
return ans;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ans;
while (root) {
if (!root->right) {
ans.push_back(root->val);
root = root->left;
} else {
TreeNode* next = root->right;
while (next->left && next->left != root) {
next = next->left;
}
if (next->left != root) {
ans.push_back(root->val);
next->left = root;
root = root->right;
} else {
next->left = nullptr;
root = root->left;
}
}
}
reverse(ans.begin(), ans.end());
return ans;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func postorderTraversal(root *TreeNode) (ans []int) {
for root != nil {
if root.Right == nil {
ans = append([]int{root.Val}, ans...)
root = root.Left
} else {
next := root.Right
for next.Left != nil && next.Left != root {
next = next.Left
}
if next.Left == nil {
ans = append([]int{root.Val}, ans...)
next.Left = root
root = root.Right
} else {
next.Left = nil
root = root.Left
}
}
}
return
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function postorderTraversal(root: TreeNode | null): number[] {
const ans: number[] = [];
while (root !== null) {
const { val, left, right } = root;
if (right === null) {
ans.push(val);
root = left;
} else {
let next = right;
while (next.left !== null && next.left !== root) {
next = next.left;
}
if (next.left === null) {
ans.push(val);
next.left = root;
root = right;
} else {
next.left = null;
root = left;
}
}
}
return ans.reverse();
}