| comments | difficulty | edit_url | tags | |||||
|---|---|---|---|---|---|---|---|---|
true |
中等 |
|
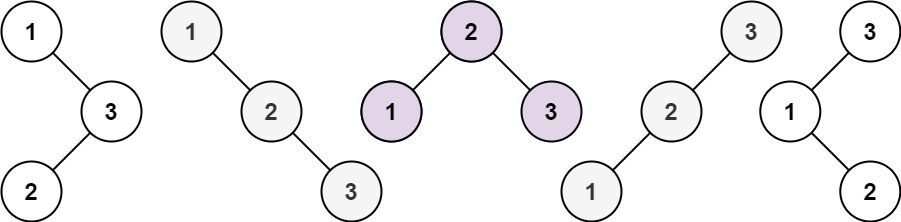
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
输入:n = 3 输出:5
示例 2:
输入:n = 1 输出:1
提示:
1 <= n <= 19
我们定义
我们可以枚举节点数
最后返回
时间复杂度
class Solution:
def numTrees(self, n: int) -> int:
f = [1] + [0] * n
for i in range(n + 1):
for j in range(i):
f[i] += f[j] * f[i - j - 1]
return f[n]class Solution {
public int numTrees(int n) {
int[] f = new int[n + 1];
f[0] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = 0; j < i; ++j) {
f[i] += f[j] * f[i - j - 1];
}
}
return f[n];
}
}class Solution {
public:
int numTrees(int n) {
vector<int> f(n + 1);
f[0] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = 0; j < i; ++j) {
f[i] += f[j] * f[i - j - 1];
}
}
return f[n];
}
};func numTrees(n int) int {
f := make([]int, n+1)
f[0] = 1
for i := 1; i <= n; i++ {
for j := 0; j < i; j++ {
f[i] += f[j] * f[i-j-1]
}
}
return f[n]
}function numTrees(n: number): number {
const f: number[] = Array(n + 1).fill(0);
f[0] = 1;
for (let i = 1; i <= n; ++i) {
for (let j = 0; j < i; ++j) {
f[i] += f[j] * f[i - j - 1];
}
}
return f[n];
}impl Solution {
pub fn num_trees(n: i32) -> i32 {
let n = n as usize;
let mut f = vec![0; n + 1];
f[0] = 1;
for i in 1..=n {
for j in 0..i {
f[i] += f[j] * f[i - j - 1];
}
}
f[n] as i32
}
}public class Solution {
public int NumTrees(int n) {
int[] f = new int[n + 1];
f[0] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = 0; j < i; ++j) {
f[i] += f[j] * f[i - j - 1];
}
}
return f[n];
}
}