Codecademy
diff --git a/‎content/scipy/concepts/scipy-integrate/terms/odeint/odeint.md
+76 b/‎content/scipy/concepts/scipy-integrate/terms/odeint/odeint.md
+76
diff --git a/‎media/odeint_solution_plot.png
21.4 KB b/‎media/odeint_solution_plot.png
21.4 KB
@@ -0,0 +1,76 @@
+---
+Title: '.odeint()'
+Description: 'Solves ordinary differential equations in SciPy using the LSODA method, automatically handling stiff and non-stiff problems.'
+Subjects:
+  - 'Computer Science'
+  - 'Data Science'
+Tags:
+  - 'Data'
+  - 'Math'
+  - 'Python'
+CatalogContent:
+  - 'learn-python-3'
+  - 'paths/computer-science'
+---
+
+The **`odeint()`** function from SciPy's [`integrate`](https://www.codecademy.com/resources/docs/scipy/scipy-integrate) module is a powerful tool for solving initial value problems for _Ordinary Differential Equations (ODEs)_.
+
+It integrates a system of ordinary differential equations using the LSODA method from the FORTRAN library `odepack`, which automatically switches between stiff and non-stiff methods based on the problem's characteristics.
+
+## Syntax
+
+The general syntax for using `odeint()` is as follows:
+
+```pseudo
+from scipy.integrate import odeint
+
+solution = odeint(func, y0, t, args=(), Dfun=None, col_deriv=0, full_output=0, ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=500, mxhnil=10, mxordn=12, mxords=5)
+```
+
+- `func`: A callable that defines the derivative of the system, ({dy}/{dt} = f(y, t, ...)).
+- `y0`: Initial condition(s) (array-like). Represents the initial state of the system.
+- `t`: Array of time points at which the solution is to be computed (1D array-like).
+- `args` (Optional): Tuple of extra arguments to pass to `func`.
+
+Other parameters are optional and control solver behavior, precision, and output verbosity.
+
+It returns a 2D [NumPy](https://www.codecademy.com/resources/docs/numpy) array, where each row corresponds to the solution at a specific time point in `t`.
+
+## Example
+
+The code below numerically solves a first-order ordinary differential equation using `odeint`. The model function defines the ODE, and `odeint` integrates it over specified time points starting from the initial condition, and the results are plotted to visualize the solution:
+
+```py
+import numpy as np
+from scipy.integrate import odeint
+import matplotlib.pyplot as plt
+
+def model(y, t):
+    dydt = -2 * y + 3
+    return dydt
+
+# Initial condition
+y0 = 5
+
+# Time points
+t = np.linspace(0, 5, 100)
+
+# Solve ODE
+solution = odeint(model, y0, t)
+
+# Plot results (indexing the solution to get the actual y values)
+plt.plot(t, solution[:, 0])  Since solution is a 2D array, we index its first column to extract the solution values.
+plt.title('Solution of dy/dt = -2y + 3')
+plt.xlabel('Time (t)')
+plt.ylabel('y(t)')
+plt.grid()
+plt.show()
+```
+
+The output plot shows the numerical solution of the ODE, illustrating how `y(t)` evolves over time:
+
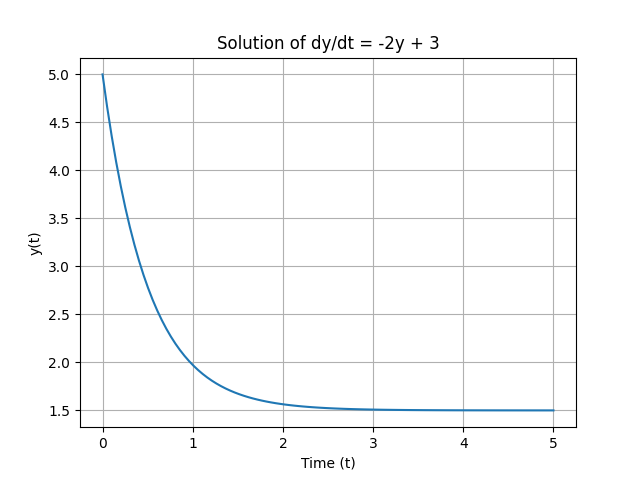+![A plot showing the solution of an ODE using odeint, with time on the x-axis and y(t) on the y-axis.](https://raw.githubusercontent.com/Codecademy/docs/main/media/odeint_solution_plot.png)
+
+`odeint()` is ideal for many scientific and engineering applications due to its robustness and flexibility.
+
+> For more advanced control or alternative solvers, consider using `scipy.integrate.solve_ivp()`, which offers a more modern API.