Skip to content

Latest commit

 

History

History
198 lines (102 loc) · 15.2 KB

翻译：Impact of the Earth Rotation Compensation on MEMS-IMU Preintegration of Factor Graph Optimization.md

File metadata and controls

198 lines (102 loc) · 15.2 KB

[TOC]

IMU 预积分中地球自转补偿的效果

摘要

在基于滤波的 GNSS/INS 组合导航系统中，精密的 IMU 机械编排需要考虑到地球自转、牵连角速度、科氏加速度等的影响；然而大多数的图优化框架中的 IMU 预积分模型都没有考虑这些因素。我们提出了一种进行了地球自转补偿的滑动窗口图优化 GNSS/INS 组合导航算法，并且评估了地球自转等对 MEMS-IMU 预积分的影响。测试了 GNSS 量测缺失，采用了有效的方法对预积分结果进行评价。结果表明，此方法预积分的精度与精密机械编排的精度相当；相比之下，IMU 在不补偿地球自转的情况下，预积分的精度显著低于机械编排的精度，有显著的精度降级。当 GNSS 中断时间为 60 秒时，工业级 MEMS 的降级可能为 200% 模块，消费级 MEMS 芯片超过 10%。此外，如果 GNSS 中断时间更长，精度降级还会更显著。

一、介绍

在本文中，我们的目标是评估 MEMS-IMU 预积分中进行地球自转补偿的效果；利用了模拟 GNSS 中断的方法，而非 VINS 或 LINS 进行分析和评估；并且以 EKF 的 GNSS/INS 组合导航解作为 INS 精确度的基准。本论文的主要贡献如下：

  • 提出了一种图优化框架下，滑动窗口 GNSS/INS 组合导航优化器，可以融合 GNSS 定位点和 IMU 预积分数据；其中我们重新定义了 IMU 预积分模型，进行了地球自转补偿。
  • 采用模拟 GNSS 中断的方法来定量评估地球自转补偿对 IMU 预积分的影响，并在开阔天空地区进行三次实地测试。
  • 为了充分展示地球自转补偿对不同等级 MEMS-IMU 的影响，我们采用了四个不同的 MEMS-IMU，包括一个消费级 MEMS 芯片和三个不同的工业级 MEMS 模块。
  • 我们将基于因子图优化的 GNSS/INS 组合导航系统和经过改进的 IMU 预积分开源，并提供上述四个数据集。

本文各章节安排如下：下一章介绍进行地球自转补偿的 IMU 预积分模型，第三章介绍 GNSS/INS 图优化组合导航模型，第四章实验和结果中定量评估地球自转补偿对 IMU 预积分的影响，在最后做出本文的研究结论。

二、重新定义的 IMU 预积分模型

大多数的 IMU 预积分模型中都忽略了地球自转，例如文献 [15]、[17]、[18]、[22]、[23]、[25]–[27]，这是对 IMU 精度的浪费，尤其是对于工业级或更高级的 IMU 来说。受到 IMU 精密机械编排的启发 ^[1]–[3]^，我们进一步重新定义了 IMU 预积分模型去补充地球自转 ^[24]^，在本章中将进行阐述，首先介绍 IMU 运动积分和预积分过程，然后介绍噪声传播和零偏的处理。

1、运动学模型

IMU 可以测量角速度 $\tilde{w}{\mathrm{ib}}^{\mathrm{b}}$ 和加速度 $\tilde{f}^{b}$（准确来说是比力），其中 $b$ 表示 IMU 载体坐标系（$b$ 系），$i$ 表示惯性坐标系（$i$ 系）。IMU 量测值受很多因素的影响，包括比例、零偏、非正交和白噪声 ^[3]^，在本论文中我们只考虑加性噪声 $n$ 和缓慢变化的零偏 $b$： $$ \tilde{\boldsymbol{w}}{\mathrm{ib}}^{\mathrm{b}}=\boldsymbol{w}{\mathrm{ib}}^{\mathrm{b}}+\boldsymbol{b}{g}+\boldsymbol{n}{g}, \tilde{\boldsymbol{f}}^{\mathrm{b}}=\boldsymbol{f}^{\mathrm{b}}+\boldsymbol{b}{a}+\boldsymbol{n}{a}, $$ 其中 $b{g}$ 和 $b_{a}$ 表示陀螺仪和加速度计的零偏， $n_{g}$ 和 $n_{e}$ 表示陀螺仪和加速度计的白噪声。

在经典的高精度 INS 运动学模型 [1]-[3] 的基础上，我们省略了特定的微小项，得到以下简化模型： $$ \begin{array}{l} \dot{p}{\mathrm{wb}}^{\mathrm{w}}=\boldsymbol{v}{\mathrm{wb}}^{\mathrm{w}}, \ \dot{\boldsymbol{v}}{\mathrm{wb}}^{\mathrm{w}}=\mathbf{R}{\mathrm{b}}^{\mathrm{w}} \boldsymbol{f}^{\mathrm{b}}+\mathbf{g}^{\mathrm{w}}-2\left[\boldsymbol{w}{\mathrm{ic}}^{\mathrm{w}} \times\right] \boldsymbol{v}{\mathrm{wb}}^{\mathrm{w}}, \ \dot{\mathbf{q}}{\mathrm{b}}^{\mathrm{w}}=\frac{1}{2} \mathrm{q}{\mathrm{b}}^{\mathrm{w}} \otimes\left[\begin{array}{c} 0 \ \boldsymbol{w}{\mathrm{wb}}^{\mathrm{b}} \end{array}\right], \boldsymbol{w}{\mathrm{wb}}^{\mathrm{b}}=\boldsymbol{w}{\mathrm{ib}}^{\mathrm{b}}-\mathbf{R}{\mathrm{w}}^{\mathrm{b}} \boldsymbol{w}{\mathrm{ic}}^{\mathrm{w}}, \end{array} $$ 其中 $w$ 表示世界坐标系（$w$ 系），北东地（NED）； $g^{w}$ 是 $w$ 系下的重力矢量；$e$ 表示地球坐标系（$e$ 系）；$w{i e}^{w}$ 是 $w$ 系下的地球自转，可以表示为： $$ \boldsymbol{w}{\mathrm{ie}}^{\mathrm{w}}=\left[\begin{array}{llll} w{\mathrm{e}} \cos \varphi_{0} & 0 & -w_{\mathrm{e}} \sin \varphi_{0} \end{array}\right]^{T}, $$ 其中， $w_{e}$ 是地球自转角速度 $7.2921158 \times 10^{-5} \mathrm{rad} / \mathrm{s}$，$\varphi_{0}$ 是初始点的大地纬度。如果我们省略地球自转 $w_{i e}^{w}$，运动学模型就与文献 [23] 一致，科氏加速度 $2\left[w_{i e}^{w} \times\right] v_{w b}^{w}$ 为提高积分精度，保留了因地球自转而产生的误差。关于运动模型的进一步简化，读者可参阅 [3]、[6]。

2、运动学积分

在积分间隔 $\left[t_{k-1}, t_{k}\right]$ 内，持续时间可以计算得到： $\Delta t_{k-1, k}=t_{k}-t_{k-1} \cdot t_{m-1}$，$t_{m}$ 是区间内两个连续的 IMU 采样时间，角增量 $\Delta \boldsymbol{\theta}{m}$ 和速度增量 $\Delta v{f, m}^{\mathrm{b}}$ 可以通过角速率 $w_{\mathrm{ib}}^{\mathrm{b}}$ 和比力 $f^{b}$ 积分来计算： $$ \Delta \boldsymbol{\theta}{m}=\int{t_{m-1}}^{t_{m}} \boldsymbol{w}{\mathrm{ib}}^{\mathrm{b}} d t, \Delta \boldsymbol{v}{f, m}^{\mathrm{b}}=\int_{t_{m-1}}^{t_{-}} \boldsymbol{f}^{\mathrm{b}} d t . $$ 也可以直接从 IMU 获得（某些 IMU 提供增量测量）。在本节中，IMU 测量值与估计偏差进行了补偿，尽管在公式中没有明确表示。此外，在整个预积分区间内，假设偏差保持不变。

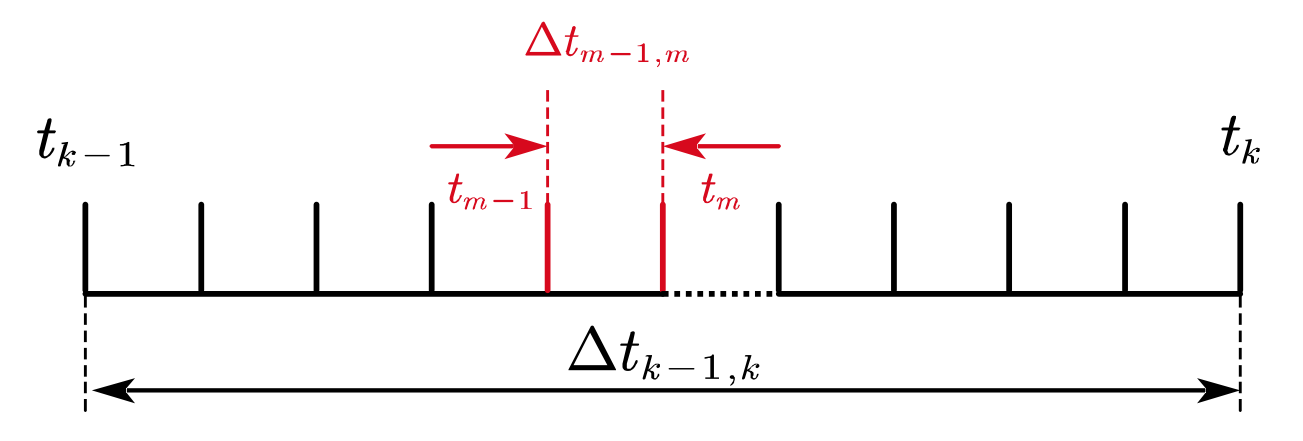
image-20240310164546105

考虑到上述的运动学模型，推导出 IMU 运动积分的计算公式如下： $$ \begin{aligned} \mathbf{q}{\mathrm{b}{m}}^{\mathrm{w}} & =\mathbf{q}{\mathrm{w}{\mathrm{i}(m-1)}}^{\mathrm{w}}\left(t_{m}\right) \otimes \mathbf{q}{\mathrm{b}{\mathrm{i}(m-1)}}^{\mathrm{w}{\mathrm{i}(m-1)}} \otimes \mathbf{q}{\mathrm{b}{m}}^{\mathrm{b}{(m-1)}} \ \boldsymbol{v}{\mathrm{wb}{m}}^{\mathrm{w}} & =\boldsymbol{v}{\mathrm{wb}{m-1}}^{\mathrm{w}}+\int_{t_{m-1}}^{t_{m}} \mathbf{R}{\mathrm{w}{\mathrm{i}(m-1)}}^{\mathrm{w}}(t) \mathbf{R}{\mathrm{b}{\mathrm{i}(m-1)}}^{\mathrm{w}{\mathrm{i}(m-1)}} \mathbf{R}{\mathrm{b}{t}}^{\mathrm{b}{\mathrm{i}(m-1)}} \boldsymbol{f}^{b} d t \ & +\int_{t_{m-1}}^{t_{m}}\left(\boldsymbol{g}^{\mathrm{w}}-2 \boldsymbol{w}{\mathrm{ie}}^{\mathrm{w}} \times \boldsymbol{v}{\mathrm{wb}{t}}^{\mathrm{w}}\right) d t \ \boldsymbol{p}{\mathrm{wb}{m}}^{\mathrm{w}} & =\boldsymbol{p}{\mathrm{wb}{m-1}}^{\mathrm{w}}+\int{t_{m-1}}^{t_{m}} \boldsymbol{v}{\mathrm{wb}{t}}^{\mathrm{w}} d t\end{aligned} $$ 其中，下标 $m$ 和 $m-1$ 表示 $t_{m}$ 和 $t_{m-1}$ 时刻，下标 $\mathrm{w}{\mathrm{i}(\mathrm{m}-1)}$ 表示上一时刻 $w$ 系相对于 $i$ 系的旋转，下标 $\mathrm{b}{i(m-1)}$ 表示上一时刻 $b$ 系相对于 $i$ 系的旋转，$\mathbf{q}{\mathrm{b}{(-m-1)}}^{w_{i(m-1)}}=\mathbf{q}{\mathrm{b}{m-1}}^{\mathrm{w}}$ 表示 $b$ 系相对于 $w$ 系的旋转，公式可改写为： $$ \begin{array}{l} \mathbf{q}{b{m}}^{w}=\mathbf{q}{w{1(m-1)}}^{w^{}}\left(t_{m}\right) \otimes \mathbf{q}{b{i}(m-1)}^{w_{i(m-1)}} \otimes \mathbf{q}{b{m}}^{b_{i}(m-1)}, \ \boldsymbol{v}{\mathrm{wb}{m}}^{\mathrm{w}}=\boldsymbol{v}{w \mathrm{~b}{m-1}}^{\mathrm{w}}+\frac{1}{2}\left[\mathbf{R}{w{(,(m-1)}}^{\mathrm{w}}\left(t_{m}\right)+\mathbf{I}\right] \mathbf{R}{\mathrm{b}{(-,-1)}}^{w_{(i,-1)}} \Delta \boldsymbol{v}{f, m}^{\mathrm{b}} \ +\left(\boldsymbol{g}^{w}-2 \boldsymbol{w}{k}^{w} \times \boldsymbol{v}{w b{m-1}}^{w}\right) \Delta t_{m-1, m}, \ p_{w_{b}}^{\mathrm{w}}=p_{\mathrm{wb}{m-1}}^{\mathrm{w}}+\frac{1}{2}\left(\boldsymbol{v}{\mathrm{wb}{m-1}}^{\mathrm{w}}+\boldsymbol{v}{\mathrm{wb}{m}}^{\mathrm{w}}\right) \Delta t{m-1, m}, \ \end{array} $$ 其中，$b$ 系旋转矢量 $\mathbf{q}{b{m}}^{b_{i(m-1)}}$ 对应增量 $\Delta \boldsymbol{\theta}{m}$，可以采用双子样算法，进一步提高运动积分的精度 ^[1]-[3]^。四元数 $\mathbf{q}{w_{i(m-1)}}^{\mathrm{w}}\left(t_{m}\right)$ 或者旋转矩阵 $\mathbf{R}{w{(m-1)}}^{w}\left(t_{m}\right)$ 是由地球自转引起的，其自转矢量可表示为： $$ \phi_{w_{i j-1 i}}^{w}\left(t_{m}\right)=-w_{i e}^{w} \Delta t_{m-1, m} . $$

3、IMU 预积分

三、基于因子图优化的 GNSS/INS 组合导航

四、实验及结果

五、结论

参考文献

  1. P. G. Savage, “Strapdown Inertial Navigation Integration Algorithm Design Part 1: Attitude Algorithms,” J. Guid. Control Dyn., vol. 21, no. 1, pp. 19–28, 1998.

  2. P. G. Savage, “Strapdown Inertial Navigation Integration Algorithm Design Part 2: Velocity and Position Algorithms,” J. Guid. Control Dyn., vol. 21, no. 2, pp. 208–221, 1998.

  3. P. D. Groves, Principles of GNSS, inertial, and multisensor integrated navigation systems. Boston: Artech House, 2008.

  4. C. Shen et al., “Seamless GPS/Inertial Navigation System Based on Self-Learning Square-Root Cubature Kalman Filter,” IEEE Trans. Ind. Electron., vol. 68, no. 1, pp. 499–508, 2021.

  5. B. Gao, G. Hu, Y. Zhong, and X. Zhu, “Cubature Kalman Filter With Both Adaptability and Robustness for Tightly-Coupled GNSS/INS Integration,” IEEE Sens. J., vol. 21, no. 13, pp. 14997–15011, Jul. 2021.

  6. Q. Zhang, X. Niu, H. Zhang, and C. Shi, “Algorithm Improvement of the Low-End GNSS/INS Systems for Land Vehicles Navigation,” Math. Probl. Eng., vol. 2013, pp. 1–12, 2013.

  7. X. Niu, H. Zhang, C. Shi, K.-W. Chiang, and N. El-Sheimy, “A proposed evaluation standard for the navigation results of MEMS INS/GPS integrated systems,” in Proceedings of the International Symposium on GPS/GNSS, 2010, pp. 1–5.

  8. C. Cadena et al., “Past, Present, and Future of Simultaneous Localization and Mapping: Toward the Robust-Perception Age,” IEEE Trans. Robot., vol. 32, no. 6, pp. 1309–1332, Dec. 2016.

  9. G. Huang, “Visual-Inertial Navigation: A Concise Review,” in 2019 International Conference on Robotics and Automation (ICRA), May 2019, pp. 9572–9582.

  10. D. Rouzaud and J. Skaloud, “Rigorous Integration of Inertial Navigation with Optical Sensors by Dynamic Networks,” Navigation, vol. 58, no. 2, pp. 141–152, Jun. 2011.

  11. D. A. Cucci, M. Rehak, and J. Skaloud, “Bundle adjustment with raw inertial observations in UAV applications,” ISPRS J. Photogramm. Remote Sens., vol. 130, pp. 1–12, Aug. 2017.

  12. D. A. Cucci and J. Skaloud, “ON RAW INERTIAL MEASUREMENTS IN DYNAMIC NETWORKS,” ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci., vol. IV-2/W5, pp. 549–557, May 2019.

  13. W. Wen, T. Pfeifer, X. Bai, and L.-T. Hsu, “Factor graph optimization for GNSS/INS integration: A comparison with the extended Kalman filter,” NAVIGATION, vol. 68, no. 2, pp. 315–331, 2021.

  14. S. Zhao, Y. Chen, and J. A. Farrell, “High-Precision Vehicle Navigation in Urban Environments Using an MEM’s IMU and Single-Frequency GPS Receiver,” IEEE Trans. Intell. Transp. Syst., vol. 17, no. 10, pp. 2854–2867, Oct. 2016.

  15. K. Eckenhoff, P. Geneva, and G. Huang, “Closed-form preintegration methods for graph-based visual–inertial navigation,” Int. J. Robot. Res., vol. 38, no. 5, pp. 563–586, Apr. 2019.

  16. W. Wen, X. Bai, Y. C. Kan, and L.-T. Hsu, “Tightly Coupled GNSS/INS Integration via Factor Graph and Aided by Fish-Eye Camera,” IEEE Trans. Veh. Technol., vol. 68, no. 11, pp. 10651–10662, Nov. 2019.

  17. T. Lupton and S. Sukkarieh, “Visual-Inertial-Aided Navigation for High-Dynamic Motion in Built Environments Without Initial Conditions,” IEEE Trans. Robot., vol. 28, no. 1, pp. 61–76, Feb. 2012.

  18. C. Forster, L. Carlone, F. Dellaert, and D. Scaramuzza, “On-Manifold Preintegration for Real-Time Visual--Inertial Odometry,” IEEE Trans. Robot., vol. 33, no. 1, pp. 1–21, Feb. 2017.

  19. A. Barrau and S. Bonnabel, “A Mathematical Framework for IMU Error Propagation with Applications to Preintegration,” in 2020 IEEE International Conference on Robotics and Automation (ICRA), May 2020, pp. 5732–5738.

  20. M. Brossard, A. Barrau, P. Chauchat, and S. Bonnabel, “Associating Uncertainty to Extended Poses for on Lie Group IMU Preintegration With Rotating Earth,” IEEE Trans. Robot., pp. 1–18, 2021.

  21. Y. Luo, C. Guo, and J. Liu, “Equivariant filtering framework for inertial-integrated navigation,” Satell. Navig., vol. 2, no. 1, p. 30, Dec. 2021

  22. S. Shen, N. Michael, and V. Kumar, “Tightly-coupled monocular visual-inertial fusion for autonomous flight of rotorcraft MAVs,” in 2015 IEEE International Conference on Robotics and Automation (ICRA)*, May 2015, pp. 5303–5310.

  23. T. Qin, P. Li, and S. Shen, “VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator,” IEEE Trans. Robot., vol. 34, no. 4, pp. 1004–1020, Aug. 2018.

  24. J. Jiang, X. Niu, and J. Liu, “Improved IMU Preintegration with Gravity Change and Earth Rotation for Optimization-Based GNSS/VINS,” Remote Sens., vol. 12, no. 18, Art. no. 18, Jan. 2020.

  25. L. Chang, X. Niu, and T. Liu, “GNSS/IMU/ODO/LiDAR-SLAM Integrated Navigation System Using IMU/ODO Pre-Integration,” Sensors, vol. 20, no. 17, p. 4702, Aug. 2020.

  26. S. Bai, J. Lai, P. Lyu, Y. Cen, and B. Ji, “Improved Preintegration Method for GNSS/IMU/In-Vehicle Sensors Navigation using Graph Optimization,” IEEE Trans. Veh. Technol., pp. 1–1, 2021.

  27. J. Henawy, Z. Li, W.-Y. Yau, and G. Seet, “Accurate IMU Factor Using

    Switched Linear Systems for VIO,” IEEE Trans. Ind. Electron., vol. 68,

    no. 8, pp. 7199–7208, Aug. 2021.

  28. L. Wang, H. Tang, T. Zhang, Q. Chen, J. Shi, and X. Niu, “Improving the Navigation Performance of the MEMS IMU Array by Precise Calibration,” IEEE Sens. J., vol. 21, no. 22, pp. 26050–26058, 2021.

  29. H. Tang, X. Niu, T. Zhang, Y. Li, and J. Liu, “OdoNet: Untethered Speed Aiding for Vehicle Navigation Without Hardware Wheeled Odometer,” IEEE Sens. J., vol. 22, no. 12, pp. 12197–12208, Jun. 2022.

  30. Agarwal, Sameer, Mierle, and Keir, “Ceres Solver — A Large Scale Non-linear Optimization Library.” [Online]. Avaliable: http://ceres-solver.org/

  31. J. Engel, V. Koltun, and D. Cremers, “Direct Sparse Odometry,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 40, no. 3, pp. 611–625, Mar. 2018