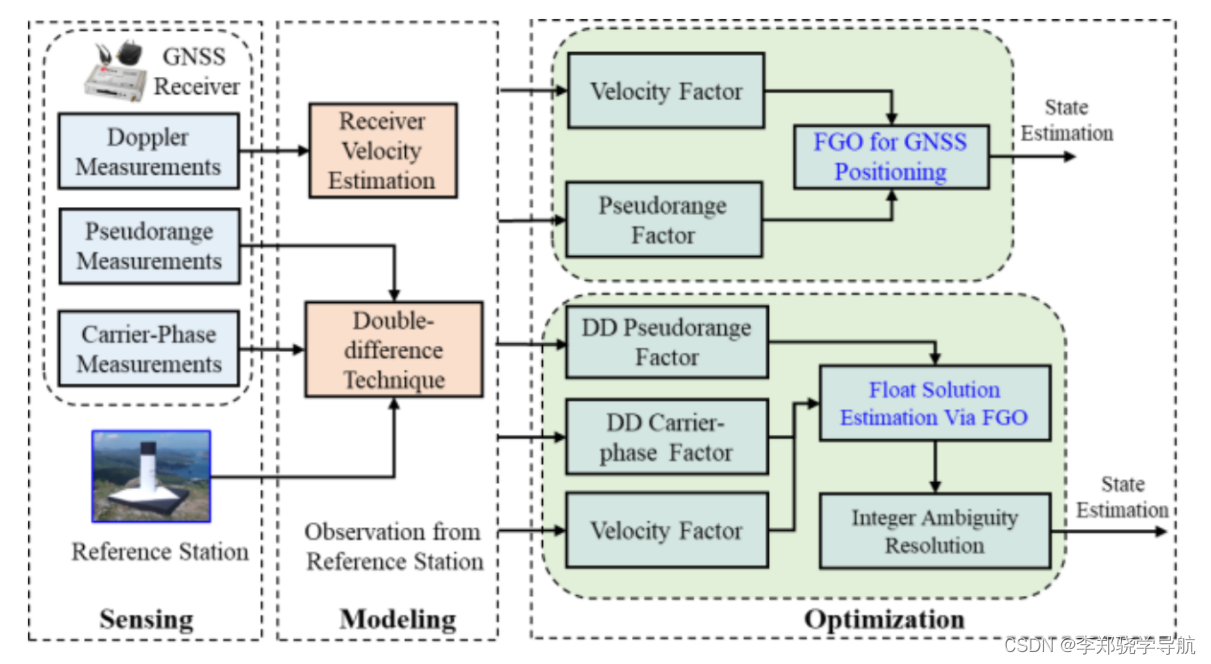
[TOC]
GNSS在诸如城市、施工现场、农田、密林等城市峡谷等遮挡环境下:
- 观测值数量和质量不稳定,卫星数甚至不足以EKF定位。
- 伪距受多路径影响严重,载波相位容易产生周跳。
- 非视距信号(NOLS)增多,且基于传统的接收机技术很难完全检测出来。
- 卫星的几何分布差,即使我们检测出来了潜在的非视距信号,然后将其排除,这会导致更差的卫星几何分布。
且由于在此类环境下,这些测量值的时间相关性更加明显,使用传统的滤波手段进行处理仅考虑前一状态的值忽略了其他历史状态值,使得定位结果更加不精确。为充分挖掘历史信息的作用,引入因子图优化(FGO)对GNSS测量值进行融合解算,该方法将伪距、载波相位、多普勒观测量添加为因子节点,引入多普勒因子连接历元间变量节点,实现解算模型的因子图优化。相较于滤波,因子图的优势体现在:
- 能够进行多次线性化计算以及多次迭代以便更好的逼近真实的模型。
- 充分利用历史观测信息,能够将所有的历史信息加入到对当前状态的计算,提高系统的精度
- 对于某些具有时间相关性的测量值更为有效,比如GNSS数据在相邻多历元之间强相关,钟的漂移在多帧内是不怎么变的,载波观测量具备类似的整周模糊度。
- 不需要设计复杂的设计矩阵,且可以灵活的增加约束关系。
- EKF有很多变种,IEKF具备因子图优化的多次迭代,如果考虑多窗口的EKF的话,就会也具备多帧数据的考量了,这样就和因子图很接近了。 但因子图很灵活,可以随意变化窗口数目,不需要复杂的重新设计观测矩阵之类的,最关键是可以很灵活的增加一些新的约束关系。
- EKF的一阶马尔科夫模型假设,前提是观测量的协方差可以准确的计算出来并且应用到EKF中,但是这个是在实际中,特别是都市环境下很难的,GNSS的观测量不确定性很大。
因子图技术的潜力,也在一个近期的Google在美国导航协会的ION GNSS+ 2021的会议上举办的一个手机GNSS定位的比赛上获得一个极大的验证,来自日本千叶工业大学的Taro Suzuki博士使用因子图技术,对手机采集的GNSS数据进行定位解算,获得了第一名。
因子图作为一种数学工具,是用因子描述多变量复杂函数的二部图,通常被用于SLAM中。图优化就是将优化问题转换成图的形式,图由边和顶点组成。边连接着顶点,表示顶点之间的一种关系。顶点表 估计问题中的未知随机变量,而因子表示有关这些变量的概 率信息,这些信息是从测量或先验信息中得出的。
因子图是一种二分图模型,它表征了全局函数和局部函数之间的关系,同时也表示了各个变量与局部函数之间的关系,以下式为例:
$$
{\begin{array}{l}
g\left(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right)=f_{A}\left(x_{1}\right) f_{B}\left(x_{2}\right) f_{C}\left(x_{1} x_{2} x_{3}\right) f_{D}\left(x_{3} x_{4}\right) f_{E}\left(x_{3} x_{5}\right)
\end{array}}
$$
将全局函数 $g$ 转化为局部函数 $f$ 的乘积,其对应的因子图如下所示:
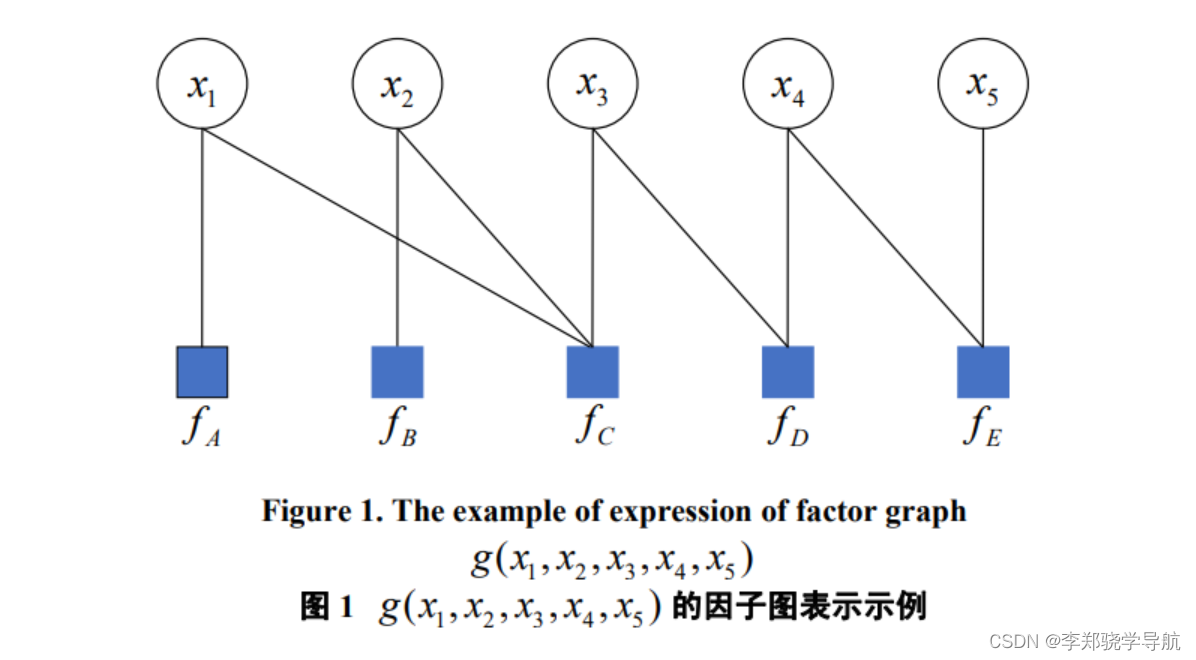
- 圆圈:每一个变量 $x$ 对应一个变量结点
- 正方形:每一个局部函数 $f$ 对应一个因子结点
- 线:当且仅当变量 $x$ 是局部函数 $f$ 的的自变量时,相应的变量节点和因子节点之间有一条边连接两个节点
在以往的状态估计问题中,往往是寻找$X$来最好地描述观测值 $Z$。根据贝叶斯法则,状态量 $X$ 和观测量 $Z$ 的联合概率等于条件概率乘以边缘概率:
$$
{P(X,Z) =P(Z \mid X) P(X)}
$$
式中:$P(Z|X)$ 为观测量 $Z$ 对应的概率;$P(X)$ 是状态量 $X$ 的先验概率。后验分布 $P(X|Z)$ 是一种常用且直观评估状态集和 观测集之间拟合程度的方法,我们求解期望的状态集可以 由通过后验分布的最大化来实现,也就是极大验后估计:
$$
\hat{X}=\underset{X}{\arg \max } P(X \mid Z)
$$
基于因子图的状态估计方法正是将状态估计理解为对系统联合概率密度函数的极大验后估计问题。 一个系统可以描述为状态方程和量测方程两部分,并将状态误差和量测误差视为零均值白噪声即:
$$
\left{\begin{array}{rr}
x_{k}=f_{k}\left(x_{k-1}, u_{k}\right)+w_{k}, & w_{k} \sim N\left(0, \Sigma_{k}\right) \
z_{k}=h_{k}\left(x_{k}\right)+v_{k}, & v_{k} \sim N\left(0, \Lambda_{k}\right)
\end{array}\right.
$$
根据正态分布的特性可以得到真实状态$k_x$和理想量测$k_z$的条件概率分布满足:
$$
\left{\begin{array}{l}
P\left(x_{k} \mid x_{k-1}\right) \propto e^{-\frac{1}{2}\left|f_{k}\left(x_{k-1}\right)-x_{k}\right|{\varepsilon{k}}^{2}} \
P\left(z_{k} \mid x_{k}\right) \propto e^{-\frac{1}{2} \mid f_{k}\left(x_{k}\right)-z_{k} |{k}^{2}}
\end{array}\right.
$$
实际中的状态量 $X$ 往往是不知道的,而当前状态下的观测 $Z$ 是知道的,也就是 $P(Z|X)$ 是知道的,因此在因子图模型中:
$$
X{k}^{}=\arg \max P\left(X_{k} \mid Z_{k}\right) \propto \arg \max P\left(X_{k}\right) P\left(Z_{k} \mid X_{k}\right)
$$
其中,$X_{k}=\left{x_{0: k}\right}$ 是状态的集合,$Z_{k}=\left{z_{0:k}^j\right}$ 是所有状态下量测的集合。若系统服从马尔科夫假设,那么:
$$
\begin{aligned}
X_{k}^{} & =\underset{X_{k}}{\arg \max } P\left(X_{k} \mid Z_{k}\right) \propto \underset{k}{\arg \max } P\left(x_{0}\right) \prod^{k}\left[P\left(x_{i} \mid x_{i-1}\right) \prod_{m_{i}}^{m_{i}}\left[P\left(z_{i}^{j} \mid x_{i}\right)\right]\right]
\end{aligned}
$$
对式取对数得到后,将式代入式可以得到,系统的状态估计可等价为全局损失函数的联合优化:
$$
X^{*}=\underset{X}{\arg\min } \sum_{i}^{k}\left{\left|f_{i}\left(x_{i-1}, u_{i}\right)-x_{i}\right|{\Sigma{i}}^{2}+\sum_{j=1}^{m_{j}}\left|h_{i}^{j}\left(x_{i}\right)-z_{i}^{j}\right|{\Lambda{i j}}^{2}\right}
$$
上式即为基于因子图优化的估计的一般表达式,其左项为系统状态转移过程,右项为量测过程,$\Sigma$和$\Lambda$分别是状态转移过程和量测过程的协方矩阵,进行求解的是状态集合 X 。对于式,可以用下图进行表示:
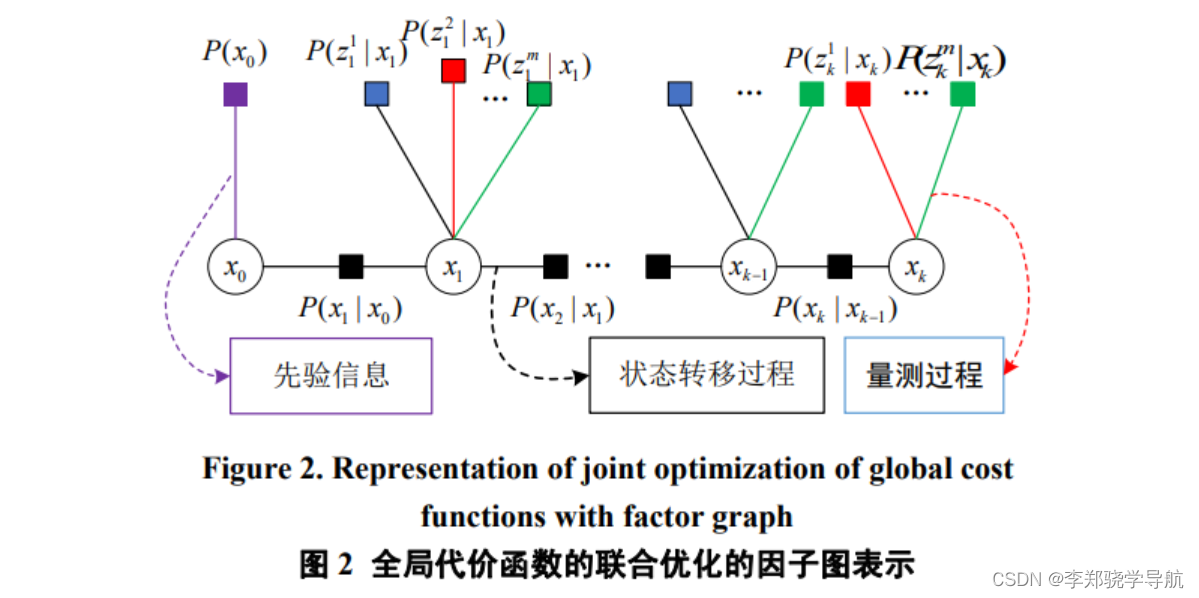
- 圆圈:变量节点,表示系统待估计的状态,对应一个变量 $x$
- 正方形:因子节点,表示先验信息、状态转移和量测过程,对应一个局部函数 $f$ ,其中:
- 紫色 $P(x_0)$ 为先验因子
- 黑色 $P(x_1|x_0) \dots P(x_k|x_{k-1})$ 为状态转移,由上一时刻状态推测下一时刻状态
- 其它为量测信息,$P(z|x)$ 表示在参数$x$的条件下得到观测值$z$
- 线:当且仅当变量 $x$ 是局部函数 $f$ 的的自变量时,相应的变量节点和因子节点之间有一条边连接两个节点
- 若在模型中加入其他传感器,只需将其添加到框架中相关的因子节点处即可
利用因子图模型对估计系统的联合概率密度函数进行表示,可以直观地反映动态系统的动态演化过程和每个状态对应的量测过程。同时,图形化的表示使系统具有更好的通用性和扩展性。
每一个观测变量在上面贝叶斯网络里都是单独求解的(相互独立),所以所有的条件概率都是乘积的形式,且可分解,在因子图里面,分解的每一个项就是一个因子,乘积乘在一起用图的形式来描述就是因子图。 整个因子图实际上就是每个因子单独的乘积。 求解因子图就是将这些因子乘起来,求一个最大值,得到的系统状态就是概率上最可能的系统状态。
先找到残差函数 $e(x)$,由因子节点可以得到我们估计的值和实际的测量值之间的差值,即每个因子 $f$ 会对应一个残差函数。根据中心极限定理,绝大多数传感器的噪声是符合高斯分布的,所以每个因子都是用高斯分布的指数函数来定义的。
$$
g(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right)
$$
指数函数对应了残差函数,包括两个部分:系统状态量和观测量。 残差函数实际上表示的是用状态量去推测的观测量与实际观测量的区别。 残差函数的表达式一般都是非线性的,可以通过改变变量 $X$ 来使残差函数最小化,残差函数最小,估计的值越符合观测值,套到因子图里面来看,因子图的求解是要所有因子的乘积最大化,
$$
\hat{X}=\underset{X}{\arg \max } \prod_{i} \exp \left(-\frac{1}{2}\left|e_{i}(X i)\right|{\Sigma i}^{2}\right)
$$
对于负指数函数形式,每一个因子乘积最大化代表里面的 $e(x)$ 最小化,对目标函数取对数,概论问题转为非线性最小二乘问题:
$$
\hat{X}=\underset{X}{\operatorname{arg} \operatorname{max}} \sum{i}\left(e_{\dot{\epsilon}}\left(x_{i}\right)\right)^{2}
$$
非线性最小二乘可以选择高斯-牛顿法、列文博格-马夸尔特或者Dogleg等迭代优化算法求解最优值,高斯-牛顿法比较简单,但稳定性较差,算法可能不收敛;列文博格-马夸尔特引入置信区间概念,约束下降的步长,提高稳定性,Dogleg也类似。问题性质较好时可用高斯-牛顿法,问题条件恶劣时选择列文博格-马夸尔特或者Dogleg。
几种非线性最小二乘解法比较:
最速下降法:目标函数在 $x_k$ 处泰勒展开,保留一阶项,$x*= - J(x_k)$,最速下降法过于贪心,容易走出锯齿路线,反而增加迭代次数。
牛顿法:二阶泰勒展开,利用二次函数近似原函数。$H*X= - J$,牛顿法需要计算目标函数的海森矩阵阵,计算量大。规模较大时比较困难。
高斯-牛顿法(GN):$f(x)$ 进行一阶泰勒展开,$f(x)$ 而不是 $F(x)$ ,高斯牛顿法用雅各比矩阵 $JJ^T$ 来作为牛顿法中二阶海森阵的近似,$HX=g$,在使用高斯牛顿法时,可能出现 $JJ^T$ 为奇异矩阵或者病态的情况,此时增量稳定性较差,导致算法不收敛。
列文伯格–马夸尔特方法(LM):基于信赖区域理论,是由于高斯-牛顿方法在计算时需要保证矩阵的正定性,于是引入了一个约束,从而保证计算方法更具普适性。$(H+\lambda I)x=g$,当入较小时,$H$ 占主导,近似于高斯牛顿法,较大时,$\lambda * I$ 占主导,接近最速下降法。
基于因子图的伪距单点定位算法使用伪距、多普勒融合算法选取的状态变量为:$X_{n}=\left[x_{n}, y_{n}, z_{n}, \delta t_{n}\right]^{T}$,$p_{u ,t}=\left[x_{t}, y_{t}, z_{t}\right]^{T}$,是某时刻 $t$ 的位置,状态变量集合为 $\chi=\left[X_{1}, X_{2}, \ldots, X_{n}\right]$。选取伪距作为测量值,多普勒的测速结果作为状态转移的约束。如下图:
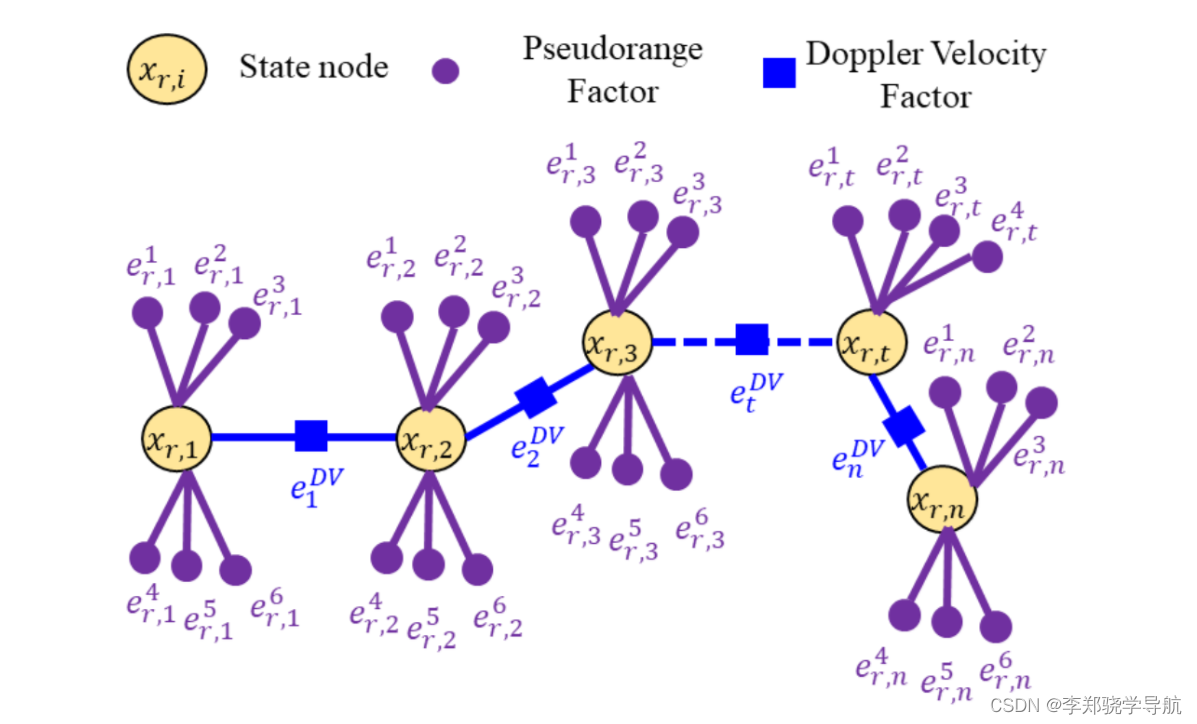
伪距的观测模型为:
$$
\rho_{u, t}^{s}=r_{u, t}^{s}+c\left(\delta t_{u, t}-\delta t_{u, t}^{(s)}\right)+I_{u, t}^{s}+T_{u, t}^{s}+\varepsilon_{u, t}^{s}
$$
其中,$r_{u, t}^{s}$ 指 $t$ 时刻的卫星 $s$ 与接收机的距离,$\delta t_{u, t}^{(s)}$、$I_{u, t}^{s}$、$T_{u, t}^{s}$ 指卫星钟差、电离层误差、对流层误差,可以通过假定的模型进估算,$\varepsilon_{u, t}^{s}$ 指随机误差。 经过误差校正后的伪距观测模型为:
$$
\rho_{c}=f_{c}\left(p_{u, t}, p_{t}^{s}, \delta_{u, t}\right)+\omega_{\rho, t}
$$
其中,$f_{c}\left(p_{u, t}, p_{t}^{s}, \delta_{u, t}\right)=\left|p_{u, t}-p_{t}^{s}\right|+\delta_{u, t}$,$\quad p_{t}^{s}$ 是卫星位置,${\omega_{\rho, t}}$ 是伪距的测量误差,其协方差矩阵为 ${\Sigma_{u,t}^{s}}$,可以通过高度角模型、信号质量等建立起协方差矩阵。 那么,伪距测量的损失函数为:
$$
\left|e_{u, t,}^{s}\right|{\sum{u, s}^{s}}^{2}=\left|\rho_{c}-f_{c}\left(p_{u, t}, p_{t}^{s}, \delta_{r, t}\right)\right|{\Sigma{u, s}^{s}}^{2}
$$
目前,GNSS的多普勒测速精度能够达到0.03m/s,远远高于伪距的精度,多普勒定速的精度影响可以忽略不计,利用多普勒测速结果对相邻历元进行约束。多普勒测速的观测模型为:
$$
v_{u, t}=f_{v, t}\left(p_{u, t+1}, p_{u, t}\right)+\omega_{v, t}
$$
其中,${f_{v, t}\left(p_{u, t+1}, p_{u, t}\right)=\left(p_{u, t+1}-p_{u, t}\right) / \Delta t}$,速度 = 两时刻的位置差值/时间间隔,$\Delta t$ 是两状态的时间间隔,即接收机接收数据频率的倒数,可以预见的是数据接收频率越高,模型越接近实际。$\omega_{v,t}$ 是多普勒测速的测量误差,其协方差为 ${\Sigma_{v,t}}$,可以通过接收机的标称测速精度或者多次实验进行调整。那么, 多普勒测速的损失函数为:
$$
\left|e_{v, t}\right|{\Sigma{v,}}^{2}=\left|v_{u, t}-f_{v, t}\left(p_{u, t+1}, p_{u, t}\right)\right|{\Sigma{v, t}}^{2}
$$
可以得到基于因子图优化的融合伪距与多普勒测量值的定位解算方法的目标函数是:
$$
\chi^{*}=\underset{\chi}{\arg \min } \sum_{t}\left|e_{v, t}\right|{\Sigma{v, t}}^{2}+\left|e_{u, t}^{s}\right|{\Sigma{u s}^{s}}^{2}
$$
其中,需要进行最优化计算的 $\chi$ 是状态的集合,而非单独的历元。
基于因子图的载波相位差分定位算法使用伪距、 载波相位、多普勒进行融合算法,选取的状态变量
$X_{t}=\left[x_{t}, y_{t}, z_{t}, \Delta \nabla N_{u r, t}^{1}, \ldots, \Delta \nabla N_{u r, t}^{m-1}\right]^{T}$,$p_{u, t}=\left[x_{t}, y_{t}, z_{t}\right]$ 是移动站的位置,${\left[\Delta \nabla N_{u r, t}^{1}, \ldots, \Delta \nabla N_{u r, t}^{m-1}\right]^{T}}$ 是 $t$ 时刻下移动站$u$和基准站 $r$ 之间 $m$ 颗共视卫星的 $m-1$ 个双差整周模糊度,状态变量的集合为 ${\chi=\left[X_{1}, X_{2}, \ldots, X_{n}\right]}$。选取伪距双差、载波相位双差作为测量值,多普勒的测速结果作为状态转移的约束。如下图:
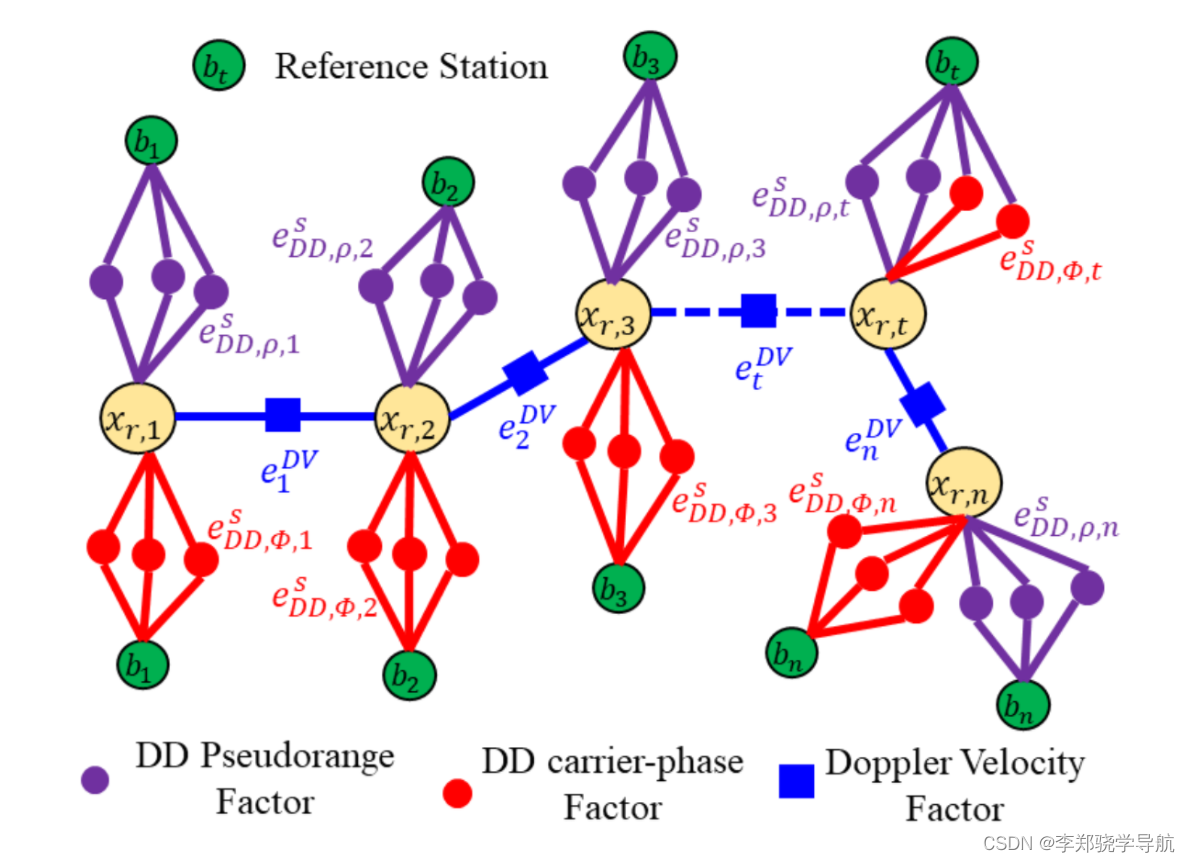
对基准站和移动站作站间差、星间差后,可以得到伪距双差的测量模型为:
$$
\rho_{D D, \rho, t}^{s}=f_{DD, \rho, t}^{s}\left(p_{u, t}, p_{b \downarrow}, p_{t}^{s}, p_{t}^{b}\right)+\omega_{DD, \rho, t}^{s}
$$
其中,$f_{D D, \rho, t}^{s}\left(p_{u, t}, p_{b, t}, p_{t}^{s}, p_{t}^{b}\right)=\left|p_{u, t}-p_{t}^{s}\right|-\left|p_{r, t}-p_{t}^{s}\right|-\left|p_{u, t}-p_{t}^{b}\right|+\left|p_{r, t}-p_{t}^{b}\right|$,${p_{t}^{b}}$ 是共视卫星中的参考星位置,为了使双差测量模型更加精确,一般选取共视卫星中高度角最大的一个作为参考星。$\omega_{DD, \rho, t}^{s}$ 是伪距双差测量模型的测量误差,是由于即使经过双差处理, 若基准站、移动站的大气情况相差过大,该测量模型仍存在误差,其协方差为 ${\Sigma_{D D, \rho, t}^{s}}$,那么,伪距双差测量损失函数为:
$$
\left|e_{D D, \rho, t}^{s}\right|{\sum{D D, \rho,}^{s}}^{2}=\left|\rho_{D D, \rho, t}^{s}-f_{D D, \rho, t}^{s}\left(p_{u, t}, p_{b, t}, p_{t}^{s}, p_{t}^{b}\right)\right|{\sum{D D, \rho, t}^{s}}^{2}
$$
同理,载波相位双差的观测模型表示为:
$$
\begin{array}{l}
\phi_{D D, \rho, t}^{s}=f_{D D, \phi, t}^{s}\left(p_{u, t}, p_{b, t}, p_{t}^{s}, p_{t}^{b}\right.
\left.\Delta \nabla N_{u r, t}^{1}, \Delta \nabla N_{u r, t}^{2}, \ldots, \Delta \nabla N_{u r, t}^{m-1}\right)+\omega_{D D, \phi, t}^{s}
\end{array}
$$
其中,$f_{D D, \phi, t}^{s}\left(p_{u, t}, p_{b, t}, p_{t}^{s}, p_{t}^{b}\right)=\left(\left|p_{u, t}-p_{t}^{s}\right|-\left|p_{r, t}-p_{t}^{s}\right|\right)-\left(\left|p_{u, t}-p_{t}^{b}\right|-\left|p_{r, t}-p_{t}^{b}\right|\right)+\Delta \nabla N_{u r, t}^{s}$,$\omega_{D D, \phi, t}^{s}$ 是载波相位双差的测量误差,协方差为 ${\Sigma_{D D, \phi, t}^{S}}$,载波相位双差损失函数为:
$$
\left|e_{D D, \phi, t}^{s}\right|{\Sigma{D D, \rho, t}^{s}}^{2}=\left|\rho_{D D, \phi, t}^{s}-f_{D D, \phi, t}^{s}\left(p_{u, t}, p_{b, t}, p_{t}^{s}, p_{t}^{w}\right)\right|{\Sigma{D D, \phi, \phi}^{s}}^{2}
$$
多普勒测速的损失函数同伪距单点定位的式子。可以得到基于因子图优化的融合伪距、载波相位和多普勒测量值的定位解算方法的目标函数:
$$
\chi^{*}=\underset{\chi}{\arg \min } \sum_{t}\left|e_{v, t}\right|{\Sigma{v,}}^{2}+\left|e_{D D, \phi, t}^{s}\right|{\Sigma{D D, \rho,}^{s}}^{2}+\left|e_{D D, \rho, t}^{s}\right|{\Sigma{D D, \rho, t}^{s}}^{2}
$$
其中,需要进行最优化计算的 $\chi$ 是状态的集合,而非单独的历元。通过对目标函数的求解即可得到各个历元的浮点解以及双差整周模糊度的浮点解,随后进行整周模糊度固定。如果能够固定再次进行计算即可得到精确的定位解,如果不能固定即用浮点解作为最终的解算结果。




