Skip to content

Latest commit

 

History

History
243 lines (172 loc) · 8.89 KB

RTKLIB 之 ppp_ar 源码阅读.md

File metadata and controls

243 lines (172 loc) · 8.89 KB

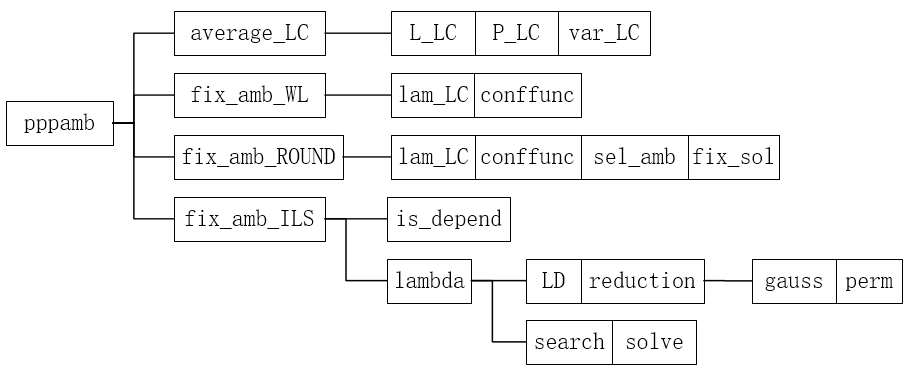
ppp_ar.c 的内容在最新版的 RTKLIB 被删除了。

[TOC]

image-20240622165232083

二、pppamb()：PPP 模糊度固定入口函数

双频的宽巷就是两频率求和，窄向就是两频率做差。宽巷组合具有较长的波长和非常小的载波方差，有利于模糊度的求解，但是放大了测量噪声；窄巷组合具有较小的距离方差，有利于基线矢量的精度，但是波长短，载波方差较大，不利于模糊度的求解。所以先固定较容易的宽巷模糊度，再固定窄向模糊度以获得更高的精度。

三、average_LC()：计算平均线性组合

L_LC()、P_LC()、var_LC()、Lam_LC() 是进行线性组合的基本函数，分别用于计算组合（三频或双频）后的载波、伪距、方差、波长。

四、fix_amb_WL()：均值取整法固定宽巷模糊度

五、fix_amb_ROUND()：取整法固定窄巷模糊度

六、fix_amb_ILS()：整数最小二乘法固定窄向模糊度

七、lambda()：最小二乘模糊度去相关法

传入参数：

int    n      I  number of float parameters      //浮点解数量
int    m      I  number of fixed solutions       //固定解数量
double *a     I  float parameters (n x 1)        //浮点参数向量
double *Q     I  covariance matrix of float parameters (n x n)   //浮点参数协方差阵
double *F     O  fixed solutions (n x m)     	//固定解
double *s     O  sum of squared residulas of fixed solutions (1 x m) //总固定残差向量

执行流程：

  • 调用LD()，首先对浮点协方差阵进行LD分解
  • 调用reduction()，lambda降相关性
  • z变换，将双差模糊度进行变换
  • 调用search(),mlambda search，结果存储在E和s中（整数解）
  • 调用solve()，逆Z变换，将在新空间中固定的模糊度逆变换回双差模糊度空间中，存储在F中
extern int lambda(int n, int m, const double *a, const double *Q, double *F,
                  double *s)
{
    int info;
    double *L,*D,*Z,*z,*E;
    
    if (n<=0||m<=0) return -1;
    L=zeros(n,n); D=mat(n,1); Z=eye(n); z=mat(n,1); E=mat(n,m);
    
    //调用LD()，首先对浮点协方差阵进行LD分解
    /* LD factorization */
    if (!(info=LD(n,Q,L,D))) {

        //调用reduction()，lambda降相关性
        /* lambda reduction */
        reduction(n,L,D,Z);

        // z变换，将双差模糊度进行变换
        matmul("TN",n,1,n,1.0,Z,a,0.0,z); /* z=Z'*a */
        
        //调用search(),mlambda search，结果存储在E和s中（整数解）
        /* mlambda search */
        if (!(info=search(n,m,L,D,z,E,s))) {
            //逆Z变换，将在新空间中固定的模糊度逆变换回双差模糊度空间中，存储在F中
            info=solve("T",Z,E,n,m,F); /* F=Z'\E */
        }
    }
    free(L); free(D); free(Z); free(z); free(E);
    return info;
}

1、reduction()：LAMBDA降相关

static void reduction(int n, double *L, double *D, double *Z)
{
    int i,j,k;
    double del;
    
    j=n-2; k=n-2;   //调序变换
    
    //对第0,1，...，k-1，k列进行降相关
    while (j>=0) {
        if (j<=k) for (i=j+1;i<n;i++) gauss(n,L,Z,i,j); //从最后一列开始，各列非对角线元素从上往下依次降相关
        del=D[j]+L[j+1+j*n]*L[j+1+j*n]*D[j+1];
        //检验条件，若不满足检验条件则开始进行调序变换
        if (del+1E-6<D[j+1]) { /* compared considering numerical error */
            perm(n,L,D,j,del,Z);
            k=j; j=n-2; //完成调序变换后重新从最后一列开始进行降相关及排序，k记录最后一次进行过调序变换的列序号
        }
        else j--;
    }
}

2、gauss()：整数高斯变换

static void gauss(int n, double *L, double *Z, int i, int j)
{
    int k,mu;
    
    if ((mu=(int)ROUND(L[i+j*n]))!=0) {
        for (k=i;k<n;k++) L[k+n*j]-=(double)mu*L[k+i*n];
        for (k=0;k<n;k++) Z[k+n*j]-=(double)mu*Z[k+i*n];
    }
}

3、perm()：条件方差重新排列

static void perm(int n, double *L, double *D, int j, double del, double *Z)
{
    int k;
    double eta,lam,a0,a1;
    
    eta=D[j]/del;
    lam=D[j+1]*L[j+1+j*n]/del;
    D[j]=eta*D[j+1]; D[j+1]=del;
    for (k=0;k<=j-1;k++) {
        a0=L[j+k*n]; a1=L[j+1+k*n];
        L[j+k*n]=-L[j+1+j*n]*a0+a1;
        L[j+1+k*n]=eta*a0+lam*a1;
    }
    L[j+1+j*n]=lam;
    for (k=j+2;k<n;k++) SWAP(L[k+j*n],L[k+(j+1)*n]);
    for (k=0;k<n;k++) SWAP(Z[k+j*n],Z[k+(j+1)*n]);
}

4、search()：mlambda搜索

static int search(int n, int m, const double *L, const double *D,
                  const double *zs, double *zn, double *s)
{
    int i,j,k,c,nn=0,imax=0;
    double newdist,maxdist=1E99,y;
    double *S=zeros(n,n),*dist=mat(n,1),*zb=mat(n,1),*z=mat(n,1),*step=mat(n,1);
    
    k=n-1; dist[k]=0.0; //k表示当前层，从最后一层（n-1）开始计算
    zb[k]=zs[k];//即zn
    z[k]=ROUND(zb[k]); y=zb[k]-z[k]; step[k]=SGN(y);    //四舍五入取整；取整后的数与未取整的数作差；step记录z[k]是四舍还是五入
    for (c=0;c<LOOPMAX;c++) {
        newdist=dist[k]+y*y/D[k];
        if (newdist<maxdist) {      //如果当前累积目标函数计算值小于当前超椭圆半径
            //情况1：若还未计算至第一层，继续计算累积目标函数值
            if (k!=0) { 
                dist[--k]=newdist;  //记录下当前层的累积目标函数值，dist[k]表示了第k,k+1,...,n-1层的目标函数计算和
                for (i=0;i<=k;i++)
                    S[k+i*n]=S[k+1+i*n]+(z[k+1]-zb[k+1])*L[k+1+i*n];
                zb[k]=zs[k]+S[k+k*n];   //计算Zk，即第k个整数模糊度参数的备选组的中心
                z[k]=ROUND(zb[k]); y=zb[k]-z[k]; step[k]=SGN(y);    //四舍五入取整；取整后的数与未取整的数作差；记录是四舍还是五入
            }
            //情况2：若已经计算至第一层，意味着所有层的累积目标函数值计算完毕
            else {
                //nn为当前候选解数，m为我们需要的固定解数，这里为2，表示需要一个最优解及一个次优解
                //s记录候选解的目标函数值，imax记录之前候选解中的最大目标函数值的坐标
                if (nn<m) { //若候选解数还没满
                    if (nn==0||newdist>s[imax]) imax=nn;    //若当前解的目标函数值比之前最大的目标函数值都大，那么更新imax使s[imax]指向当前解中具有的最大目标函数值
                    for (i=0;i<n;i++) zn[i+nn*n]=z[i];  //zn存放所有候选解
                    s[nn++]=newdist;    //s记录当前目标函数值newdist，并加加当前候选解数nn
                }
                else {  //若候选解数已满（即当前zn中已经存了2个候选解）
                    if (newdist<s[imax]) {  //若当前解的目标函数值比s中的最大目标函数值 
                        for (i=0;i<n;i++) zn[i+imax*n]=z[i];    //用当前解替换zn中具有较大目标函数值的解
                        s[imax]=newdist;    //用当前解的目标函数值替换s中的最大目标函数值
                        for (i=imax=0;i<m;i++) if (s[imax]<s[i]) imax=i;    //更新imax保证imax始终指向s中的最大目标函数值
                    }
                    maxdist=s[imax];    //用当前最大的目标函数值更新超椭圆半径
                }
                //在第一层，取下一个有效的整数模糊度参数进行计算（若zb为5.3，则z取值顺序为5,6,4,7，...）
                z[0]+=step[0]; y=zb[0]-z[0]; step[0]=-step[0]-SGN(step[0]);
            }
        }
        //情况3：如果当前累积目标函数计算值大于当前超椭圆半径
        else {
            if (k==n-1) break;  //如果当前层为第n-1层，意味着后续目标函数各项的计算都会超出超椭圆半径，因此终止搜索
            else {  //若当前层不是第n-1层
                k++;    //退后一层，即从第k层退到第k+1层
                z[k]+=step[k]; y=zb[k]-z[k]; step[k]=-step[k]-SGN(step[k]); //计算退后一层后，当前层的下一个有效备选解
            }
        }
    }
    // 对s中的目标函数值及zn中的候选解进行排序（以s中目标函数值为排序标准，进行升序排序）
    // RTKLIB中最终可以得到一个最优解一个次优解，存在zn中，两解对应的目标函数值，存在s中
    for (i=0;i<m-1;i++) { /* sort by s */
        for (j=i+1;j<m;j++) {
            if (s[i]<s[j]) continue;
            SWAP(s[i],s[j]);
            for (k=0;k<n;k++) SWAP(zn[k+i*n],zn[k+j*n]);
        }
    }
    free(S); free(dist); free(zb); free(z); free(step);
    
    if (c>=LOOPMAX) {
        fprintf(stderr,"%s : search loop count overflow\n",__FILE__);
        return -1;
    }
    return 0;
}